
§1 楔子
「不由前塵所起知見,明不循根,寄根明發,由是六根互相為用。阿難,汝豈不知?今此會中,阿那律陀,無目而見;跋難陀龍,無耳而聽;殑河神女,非鼻而聞香;驕梵缽提,異舌知味;舜若多神,無身覺觸;摩訶迦葉,久滅意根,圓明了知,不因心念。」……楞嚴經。
大約1994年,一位同事跟我說,想要指導學生證明等周長定理:
周長固定的平面簡單(自身不相交)封閉曲線中圓的面積最大。
我試問:等周長定理可以用初等數學證明嗎?
後來到清大進修40學分班,跟全任重先生學動態幾何,對反演幾何有比較深入的接觸,反演幾何是史坦那(Jacob Steiner 1796~1863)於1830年發展的。
同時跟沈昭亮先生學到史坦那對稱化法,1838年史坦那就是用對稱化法"證明"了等周長定理,這是最早用綜合幾何的方法證明等周長定理的人。
這時候對等周長定理才有比較深入的理解。
§2 歷史背景
具有相等面積的平面圖形中,以圓形周長最短。
或者它的等價敘述"周長固定的平面圖形中,以圓的面積最大。"這叫做等周長定理(isoperimetric theorem)。
矩形的等周長定理公元前300年的甌幾里得已經知道了。
後來禪得羅斯(Zenodorus 200BC~140BC)寫了一本"等周圖形"的書,但流失了。
公元300年帕伯斯(Pappus of Alexandria AD290~AD350)重新敘述並證明他的結果。
事實上,他認為他證明了等周長定理。 一個周長為L,所圍區域面積為A的閉曲線,其等周商IQ(Isoperimetric Quotient)定義為與具有相同周長的圓的面積比。
顯然一個平面圖形的等周商=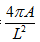
匈牙利數學家波里亞(G.Pólya 1887~1985)寫了好幾本名著,他把等周長定理改成這樣: 一個平面圖形的等周商小於或等於1 。
換句話說,算算各種平面圖形,圓的IQ=1,是最大的。

 §3 史坦那對稱化法
§3 史坦那對稱化法
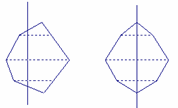
所謂史坦那對稱化法是這樣的:
考慮一個凸體,在給定的方向上畫一條直線L,移動每條垂直於此直線的弦,使得L成為此弦的垂直平線,平移後的弦的端點構成一個新的對稱圖形,它與原圖形有相同的面積,但是周長較小。(稱為反射原理,跟後面習作有關。)
以下是史坦那關於等周長定理證法的脈絡:
- 如果圖形不是凸的,用反射原理可以找到一個周長相等,但是面積較大的圖形。
- 一個凸的圖形,如果不是圓形,一定存在一軸,使該圖不對稱,則我們對該軸作史坦那對稱化,則找到一個面積相等﹑周長較小的圖形,所以等周長定理成立。
(註:此處反射原理請參看凡異出版社出版的幾何不等式 p.26,67。)
史坦那並沒有證明最大面積的存在性,所以維爾斯特拉斯(Karl Weierstrass 1815~1897) 必須進一步發展微積分來證明。
§4 數學與物理交會的地方
1973年我大學二年級,當時微分幾何是黃海先生教的,課程教完後他說要到國外念書,念什麼呢?
聽說是去念"聽音辨形"。
沒錯,就是聽到一個振動體發出的聲音,就可以知道它的形狀。
武俠小說中"聽音辨位"是修練暗器的功夫,"聽音辨形"聽起來蠻高級的。
拿一把吉他,按住弦中點所發出的音調比空弦時高八度,這件事古希臘的畢達哥拉斯早已知道了。
十七世紀是分析學的肇始時代,分英國與歐陸兩學派。
英國學派宗主是牛頓,1714年牛頓的學生,泰勒(Brook Taylor 1685-1731)解決了弦振動的基本頻率公式,它完全由弦的長度,拉力與密度決定。
1746年,法國數學家達朗貝爾(Jean Le Rond dAlembert 1717-1783)證明了琴弦的許多種振動都不是正弦式駐波。
1748年,瑞士數學家尤拉(Euler 1707-1783)推出了琴弦的"波動方程式",並求出其解。
到這裡,我們可以說:聽到琴弦發出的頻率可以知道他的"形狀"了。
解決了一維的問題,當然要處理二維的東西了。
二維振動的樂器中,自然就想到鼓了。
1795年尤拉開始研究鼓的問題,並再度導出一個波動方程式。
那麼聽到鼓音的頻率可以知到鼓的形狀嗎?
瑞利爵士(Lord Rayleigh 1842-1919)把許多等面積,不同形狀的羊皮均勻的繃在鼓上,然後測量它們發出的主頻率,得到"圓具有最低的主頻率"這樣的結論。
於是他提出瑞利猜測:聽到一個振動體發出的聲音,就可以知道它的形狀。
這是由觀察﹑歸納﹑類比到猜想的過程,當然數學家想要從猜想得到證明。
1966年,波蘭數學家卡克(Mark Kac 1914~1984)重提這個問題:你可以聽到鼓的形狀嗎?(一個黎曼流形是否由其拉普拉斯譜決定?)瑞利猜測再度引起注意。
因此可知黃海先生就是為瑞利猜測出去的。
結果如何呢?
1992年(大約是黃海先生出國的20年後),達特茅斯學院的女教授戈登(Carolyn S.Gordon)與瑋伯(David L.Webb)﹑沃伯特(Scott Wolpert)找到了反例。
換句話說,瑞利猜測已得到否定的答案,可以找到不同形狀的鼓,它們聽起來是一樣的。
但這不是重點,整個數學史的發展一直都是這樣的,結論其實並不是最重要的,重要的是從求解的過程中我們會得到很多方法或數學內容。
數學的等周長定理與物理的瑞利的膜片實驗為什麼有那麼密切的關聯呢?
理由是因為它們都來自同一個宇宙本體。
所謂"人法地﹑地法天﹑天法道﹑道法自然。"。你說呢?
有尤拉的波動方程式,才有馬克斯威爾的電磁學,有電磁學才有電視機,我們日常生活用品的背後有很嚴密的數學支持著,數學是文化重要的一環。
我們是用數學的模式解讀自然。
§5 後記
具有等體積的所有立體中,以球有最小的表面積,這是等周長定理的延伸。
其實這件事小貓也知道,君不見寒冬來臨,貓都是蜷曲著身體嗎。
體積固定,表面積愈小,則散熱愈少,小貓以此保持體溫。
等周長定理的名稱是笛卡爾最先在"思想的法則"一書中提出的。
笛卡爾另一本比較有名的著作是"我思故我在"。
其實那沒什麼了不起,我很小的時候有一次走路不小心,腳趾踢到石頭,痛入心扉,就知道"我痛故我在"的道理了。
文章刊登在龍騰數亦優雜誌
§6 參考資料
- 幾何不等式---凡異出版社 p26,67
- 大自然的數學遊戲(天下文化) p.90
- 牛頓雜誌1992/9,112期 p.141
- 從肥皂泡到液晶生物膜--牛頓出版社 p.120
- 數學與猜想--九章出版社 p.182
- 數學傳播季刊 第十卷第一期—史坦那的生平 p.8
- Mark Kac(Can one hear the shape of a drum?American Mathematical Monthly 73 (1966) 1-23)
- 等周長定理與不等式
- You cant always hear the shape of a drum
- Drums that sound alike
- 數學傳播季刊 第30卷第4期 我們可以聽出鼓的形狀嗎?(Peter Greiner 演講) p.34
限會員,要發表迴響,請先登入











