River Flows In You by Miranda Boumedia on Tidal.com

---

數學是一種演譯的學問

從定義出發 定理的內容 方法 意義 通過證明 實例 應用 與物理的闡釋 得以完成

 

Jacobi(向量)場得從測地線(geodesic)出發

Jacobi場的定義

 

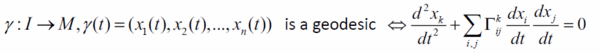
§一個實例

 

§ Jacobi 場與潮汐力(Tidal forces)

在廣義相對論中，兩物體開始時沿兩平行軌道(trajectory)運動，潮汐力(tidal force)的存在(時空曲率的存在)會造成軌道接近或遠離，在此兩物體間產生相對加速度。

因此，所謂的測地線偏離效應，它是引力相互作用的一種體現。

數學上，廣義相對論中的潮汐力用黎曼曲率來描述，而一物體在重力影響下的軌道稱為測地線。

測地線偏離方程式描述兩鄰近測地線之間黎曼曲率張量與相對加速度的關係。

或者說，沿測地線C的Jacobi場的作用在於度量鄰近C的測地線偏離C的速度。

在微分幾何中，測地線偏離方程式通常稱為Jacobi場方程式。

辛格(John Lighton Synge 1897~1995)是最早研究黑洞內部的物理學家之一，稱Jacobi fields方程是測地線偏離方程 在引力波的研究中有應用。

 [引力波百年漫談] 盧昌海

 

黑洞是重力場中的奇異點(singularity)

 

§Jacobi場與變分法

 

[大域微分幾何 Ch30 ] CMC上的Jacobi場與Morse Index定理

1. CMC(常均曲率)曲面上Jacobi場的分佈 
2. Morse Index定理 
3. Geodesics的穩定 
4. Jacobi場的multiplicity 分佈 共軛邊界 
5. Sobolev Theory 
6. 值譜分解

§應用

1. Jacobi fields and tidal effects in Kerr Spacetime(一個旋轉的黑洞)
2. Applications of Jacobi fields to the Billiard Ball Problem
3. Applications of Jacobi fields to Normal Contact Lorentzian Manifolds

---

後記

1. 常均曲率(cmc)曲面離我還很遙遠
2. Spacetime and Geometry by Sean Carroll 是一本廣義相對論的書 第四章 重力 很難 尋找靈感中

---