Kinderszenen(童年即景)是Bobert Alexander Schumann(1810~1856)的作品

我的童年 1968/9黛娜颱風之前 是在台東 賓朗村的半山腰度過 貧窮而快樂的童年

山下的河流是抓魚 捕鳥 玩耍  採野果的秘境

山的對面是牧場 我可以看到對面的羊群 橄欖樹

往山更高處爬 山頂是一廣闊的平台 越過平台 可以到"高台"看布袋戲

---

一曲面上連接兩點 有最短距離的曲線，稱為測地線(geodesic)。

這樣的觀念在高等數學很重要，在初等數學 我們找到一些例子。

左圖一隻螞蟻從一圓柱體的糖罐底部P點沿著柱體側面旋轉往上爬到Q點，若柱體高PQ =8公分，底面圓周長6公分，求螞蟻爬行的最短距離___公分。

這個例子也說明測地線不一定是最短路徑，螞蟻直接從P往上走到Q，顯然距離比較近。

這同時也說明了曲面上連接兩點的測地線不是唯一的

 

在廣義相對論中，一個自由粒子走的路徑(世界線)是測地線，此時黎曼流形的度量決定了空間的曲率。

等價(效)原理(equivalence principle)指出重力場決定伽利略時空的曲線，這些曲線是對稱聯絡(Cartan connection)的測地線。

 

測地線有多種求法 :

§ 1.古典微分幾何如下

 

§ 2.能量的Euler-Lagrange方程

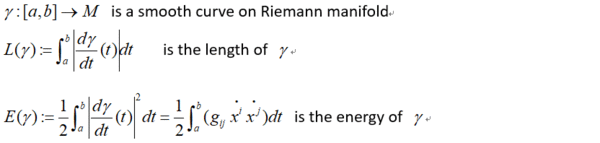
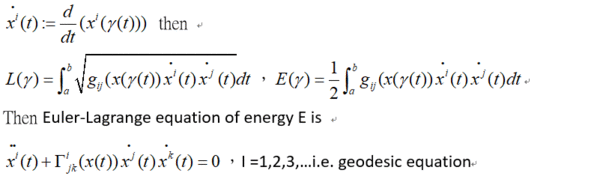
就是說 質點走花最小能量的路徑

此時測地線稱為作用量S的critical point,證明的細節就省略了

 

§ 3.從平行移動 協變微分

 

§ 4.古典力學 最小對耦原理(minimal-coupling principle)

就是說 粒子在不受力的情形下

(1)寫出平直(歐氏)空間的運動方程式(直線) 

(2)把加速度中的微分改成協變微分

(3)得到彎曲空間中的運動方程式(即 測地線方程式)

 

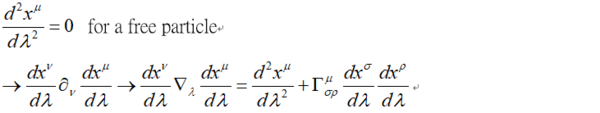
§ 5.從熱力學 heat flow方程看測地線

 

§ 6.變分法(variation),這是常見的方法 暫略

 

值得一提的是

(1)(2)(3)式看起來很像 其實它們是互相決定的

 

§

1. 這裡有Hyperbolic plane的測地線 有一個解微分方程的巧妙的方法
2. 這裡的Jacobi field 是關於測地線偏離
3. 這裡有一個有趣的蟲洞的測地線 
4. 這裡有帶電黑洞的測地線
5. 何謂Geodesic flow 這裡有小小的說明
6. 我們從geodesic出發 建構exponential map 得到一個局部的normal coordinates 以簡化計算
7. 一直用到Euler-Lagrange方程式 參考之

 

§ 大圓(例如 赤道 經線)顯然是球面S^2 的測地線 以下的計算只是一個習作

1.

 

2.參考書目(5)p.154

 

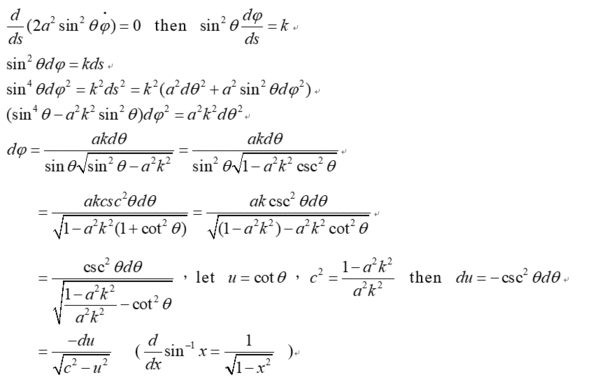
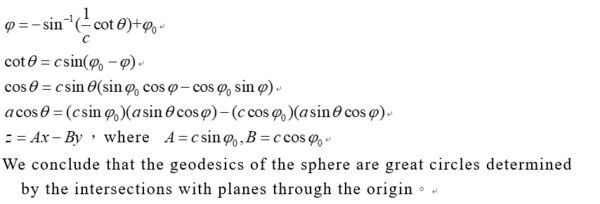
§ 輪胎面(torus)上的測地線就複雜多了

 

§ 參考書目

1. An Introduction to Riemannian Geometry     by Jose Natario
2. 大域微分幾何     黃武雄
3. Spacetime and Geometry   by Sean Carroll   [cf ProfoundPhysics]
4. Riemannian geometry and geometric Analysis    by Jurgen Jost p.23
5. Differential Geometry in Physics    by Gabriel Lugo p.154 有旋轉面的測地線
6. Differential Geometry 杜武亮       p.110 

---