 當雨滴落在荷葉上
當雨滴落在荷葉上
§ Obstacle problem for MCF
[Generic mean curvature flow with obstacles]是高棹 圭介教授之作
我想成雨滴滴落荷葉 因為最近在看均曲率流(mean curvature flow) 看看AI怎麼說
【水調歌頭】雨滴與荷葉
細雨墜青圃,宛轉落蓮心。一珠懸止不下,圓潤自成陰。
不陷不浮如夢,似問誰人設限,曲面止於今。
若論此中理,障礙悄然臨。不穿透,亦不退,形自斂。
欲隨曲率而動,卻被葉縫禁。
漸悟自由邊界,乃是心弦所在,變化總相尋。
從此觀雨滴,亦可識真深。
雨滴掉在荷葉上算得上是遇到障礙的MCF?
ChatGPT:
當雨滴落在荷葉上:
- 表面張力作用:雨滴不會立刻被荷葉吸收,而是形成球形水珠,這與最小曲面的性質有關。
- 荷葉的彎曲與撐起:荷葉會因雨滴重量微微下陷或撐起。
- 雨滴會滑動:若荷葉傾斜或彎曲,雨滴會沿著曲面滑動甚至彈走。
這些現象都和曲面形變與接觸幾何(contact geometry)有關,
與「障礙問題(obstacle problem)」的某些數學結構產生共鳴。
障礙問題與MCF 障礙問題(Obstacle problem)是變分法與偏微分方程(PDE)中的一類問題,典型情況是:
找出一個函數,使得它在某區域內滿足一定的偏微分方程,同時又不能低於某個給定的障礙函數。
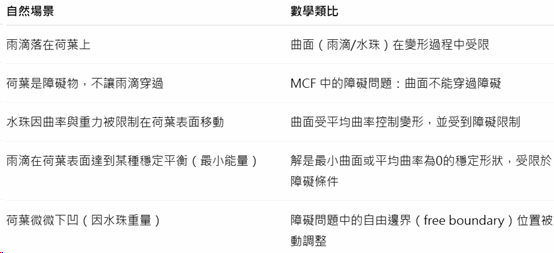
雨滴在荷葉上實際上可以被視為一種受阻的最小曲面問題(即一個液滴表面在受到荷葉限制的情況下達到最小能量配置)。
若考慮水滴落下後再擴散與收縮,那就會像MCF障礙問題的動態版本。
雨滴落在荷葉上」的現象可視為一種自然界的平均曲率流障礙問題具象化:
一個曲面(雨滴)在能量趨小的驅使下嘗試演化,但受到一個障礙(荷葉)限制,不得穿越,最終達成平衡或被迫改變演化路徑。
這正是MCF障礙問題的核心精神。
DeepSeek:
嚴格來說,MCF障礙問題通常研究的是曲面演化時避開固定障礙(如平面),而雨滴問題還需考慮:
- 流體動力學(如黏性耗散)。
- 三相接觸線的複雜性(非純幾何約束)。
雨滴在荷葉上的行為可以啟發式地類比為MCF的障礙問題,尤其在靜態形狀或接觸線約束方面。
但嚴格數學模型需擴展經典MCF,納入流體力學和表面化學效應。
若僅關注幾何演化而忽略動態細節,這一類比可作為理解曲面受障礙約束的直觀例子,但需注意其局限性。
看起來似乎 DeepSeek比較嚴謹
限會員,要發表迴響,請先登入









