 心情故事
心情故事
在數據機發出軋軋響的年代 申請網路要到教育局辦理 還得學校教務主任簽字
"這網際網路對教育有幫助嗎?" 主任如是問 我笑笑 沒有回答
我在[一個flow的故事]中有一個問題
為何常態分佈(normal distribution)的機率密度函數會是一個熱傳播方程的解 ?
一直放在心中 今天問一下DeepSeek
它的回答相當令人滿意 跟各位分享
我問 Why the solution of heat equation is the Normal distribution?
DeepSeek如是回答 :
先貼心地解釋 何謂heat equation 與 Fundamental solution
然後說 "為什麼是常態分佈"
差不多就是先介紹了新娘 然後說 為何新郎就是你
The connection between the heat equation and the normal distribution arises from the properties of diffusion:
- Central Limit Theorem:
The normal distribution describes the distribution of sums of many small,independent random variables。
In diffusion,particles move randomly,and their displacements over time can be thought of as the sum of many small,random steps。
This leads to a Gaussian distribution of particle positions。 - Infinite Domain and Symmetry:
In an infinite domain,the solution must be symmetric and spread out over space as time progresses。
The Gaussian function is the only function that satisfies these properties while also being a solution to the heat equation。 - Fourier Transform:
The heat equation can be solved using the Fourier transform。
The Fourier transform of a Gaussian function is another Gaussian,which makes it a natural solution to the heat equation。 - Maximum Entropy Principle:
The normal distribution maximizes entropy for a given mean and variance,which aligns with the idea that diffusion tends to spread out energy or particles in the most "disordered" way possible。
Generalization
For an arbitrary initial condition u(x,0)=f(x) u(x,0)=f(x), the solution to the heat equation can be expressed as a convolution of the initial condition with the Gaussian kernel:
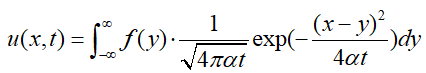
This shows how the Gaussian kernel "spreads out" the initial condition over time,further emphasizing the connection between the heat equation and the normal distribution。
In summary,the normal distribution is the solution to the heat equation because it naturally describes the process of diffusion,which involves the random spreading of particles or energy over time。
意思是說渾然天成!
The properties of the Gaussian function align perfectly with the physical and mathematical requirements of the heat equation。
高斯函數是熱(PDE)方程之良配!
限會員,要發表迴響,請先登入












