<Python練習 時間序列的整合移動平均自迴歸模型(ARIMA)>
一、整合移動平均自迴歸模型(Autoregressive Integrated Moving Average Model,ARIMA)
依照英文縮寫字母,依序說明何謂ARIMA模型
(一)AR,Autoregressive,自迴歸
AR模型是先前曾練習過的主題,是指時間序列資料本身,會受其先前自身資料數值的影響.假設Y為分析的時間序列,則
Yt = α+β1Yt-1+β2Yt-2+…+βpYt-p+ɛt
(二)I,Integrate,整合
I是指整合AR與MA模型,AR說明如前,MA則如後說明.
(三)MA,Moving Average,移動平均
所謂MA,是指時間序列資料本身,會受其先前各期按AR模型的預測殘差值(ɛ)的影響,即
Yt = α+ɛt+Φ1ɛt-1+Φ2ɛt-2+…+Φqɛt-q
上式中,各期的ɛ是指
Yt = β1Yt-1+β2Yt-2+…+β0Y0+ɛt
.
.
Yt-q = β1Yt-q-1+β2Yt-q-2+…+β0Y0+ɛt-q
(四)ARIMA模型的數學表示式為:
Yt = α+β1Yt-1+β2Yt-2+…+βpYt-p+ ɛt+Φ1ɛt-1+Φ2ɛt-2+…+Φqɛt-q
(五)有一點要特別注意,無論是AR或是MA模型,其前提是只能在具穩定性 (stationary)的時間序列資料中操作.所謂穩定性,是指資料的統計特性,如平均數、變異數等,不會隨著時間而改變.若原始資料本身為非穩定性(non-stationary),須先經一些數學調整過程使其具穩定性後,始能套用AR或MR模型.如何將非穩定性資料調整成穩定性資料,有許多統計上的數學技巧,在先前的AR模型練習過一些方式.但目前要練習的ARIMA模型,是直接利用Python的statsmodels模組提供的套件,該套件內建以差分進行資料的穩定性調整,這是要使用statsmodels模組前要注意的地方.
二、台鐵通勤列車乘客人數預測練習
延續先前的練習:
(一)抽離季節性因素,用添加式的古典分解法(additive classical decomposition),將台鐵通勤列車乘客人數資料分拆成長期趨勢(trend)、季節性因素(seasonality)及噪音(noise)三組數據
(二)利用分拆出的trend資料來訓練ARIMA模型,再將訓練後的ARIMA所演算的trend預測值,再加上各期對應的seasonality,即可得出各期的預測台鐵通勤列車乘客人數.
三、ARIMA模型
(一)套件匯入
from statsmodels.tsa.arima_model import ARIMA
(二)決定d,p,q的參數值
所謂的d,p,q,其分別代表:
l d:使資料調整成具穩定性的差分階層(order)
l p:AR模型的最適自身資料遞延期數(lag)
l q:MA模型的最適的殘差值遞延期數
- 1. 如何決定d值
如前面所說,運用AR或MA模型的前提,是資料需具穩定性(stationary),故d值的選定,讓資料調整成具穩定性,是使用ARIMA模型的最關鍵一步.如何檢定穩定性,有不同的統計檢定法,在Python世界裏,也有許多方法,在此使用Python的迷人之處-懶人包,直接拿他人已寫好的套件來用
(1) 套件匯入
from pmdarima.arima import ndiffs
ndiffs()函式是個很簡便的懶人包,會直接幫我們算出推薦的差分階層數(order)
(2) 選擇穩定性統計檢定模型
如前所述,有不同的統計檢定法用來檢定資料是否具有穩定性,而不同的檢定性有其特定的資料性質假設及限制,所以同一個資料集,在不同的檢定法觀點下,將資料穩定化所需的差分階層(order)可能會不同.ndiffs()函式內建kpss,adf,pp三種統定檢定法,利用’test’參數來選擇要使用的檢定法.這次練習使用先前在練習AR模型時曾用過的adf檢定法
(3) 選擇差分階層(order)範圍
ndiffs()函式預設在0~2範圍內算出推薦的d值,但可用’max_d’這個參數來變更搜尋範圍,如設定max_d=5,搜尋範圍即改為0~5區間內.一般來說,order>2時,資料雖在’數學’上達到穩定性要求,但在’統計關聯性’上,通常業較無實質上的意義
(4) 語法
ndiffs(資料集, test=’adf’,max_d=5)
直接拿trend當資料集,得出d=1
(5) 有一點要注意,ndiffs()雖提供在搜尋範圍內,統計檢定結果比較好的推薦d值,但並不保證經d階差分後的資料集一定具有非常好的穩定性.在之前的AR模型練習中,我們已看到,trend資料經一階差分後,在adf檢定下,其穩定性尚非十分理想
- 2. 如何選擇 AR模型的p值
可利用資料集的pacf視覺化圖形來輔助
(1) pacf是指偏自相關函數(partial autocorrelation function),其背後的統計上數學涵義,先略過直接看其圖形結果
(2) 套件匯入
from statsmodels.graphics.tsaplots import plot_pacf
(3) 語法
plot_pacf(trend.diff())
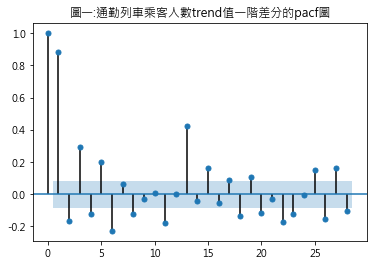
因AR模型的資料需具穩定性,故plot_pacf()函式需放入業經穩定性調整過後的資料,其中,trend.diff()是指通勤列車乘客人數trend值的一階差分
從圖一可發現,遞延期數在15期時仍具統計顯著性(圖形仍掉在陰影區外).先前的AR模型練習,模型擇定最適遞延期數為18期
- 3. 如何選擇MA模型的q值
可利用資料集的acf視覺化圖形來輔助
(1) acf是指自相關函數(autocorrelation function),其背後的統計上數學涵義,先略過直接看其圖形結果
(2) 套件匯入
from statsmodels.graphics.tsaplots import plot_acf
(3) 語法
plot_acf(trend.diff())
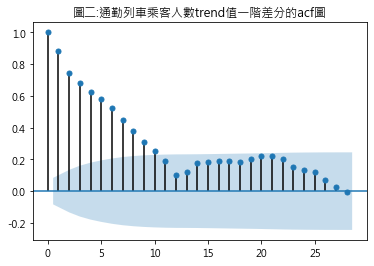
因MA模型的資料需具穩定,故plot_acf()函式需放入業經穩定性調整過後的資料,其中trend.diff()是指通勤列車乘客人數trend值的一階差分
從圖二可發現,遞延期數大於9時,已不具統計顯著性(圖形已掉到陰影區)
(三)Python ARIMA模型操作
- 1. 語法
模型 = ARIMA(trend資料集, order=(p,d,q))
訓練後模型 = 模型.fit(disp=0)
- 2. 如何找出最適的p,q組合
(1) 雖然可用pacf及acf判斷個別p,d值大致範圍,但我們希望利用ARIMA模型預測時,選用的(p,d,q)參數組合訓練出的模型能有較好的效能,這時可利用訓練後模型的Akaike information criterion(AIC)進行檢測,AIC愈低,模型效能愈好.Python提供的套件已提供模型訓練後的aic屬性(property),我們可直接下「訓練後模型.aic」這個指令得知訓練後模型的AIC值
(2) 因測試時,若p>10或q>8時,Python就會回報資料集為非穩定性(non-stationary),故在p<=10 span="" style="font-family:, serif" data-mce-style="font-family: , serif;">及q<=8 span="" style="font-family:, serif" data-mce-style="font-family: , serif;">範圍內,找出AIC值最低的(p,d,q)組合
*語法:
p_value = 1
q_value = 0
aic_value = np.Inf #先設定為無窮大
for p in range(1,11):
for q in range(9):
model = ARIMA(trend_arima,order=(p,1,q),freq=None)
model_fit = model.fit(disp=0)
if model_fit.aic < aic_value:
p_value = p
q_value = q
aic_value = model_fit.aic
(3) 依上法,找出使AIC值最低的(p,d,q)組合為(10,1,8)
- 3. ARIMA模型預測
(1) 設定模型
模型 = ARIMA(trend訓練資料集, order=(10,1,8))
*trend訓練資料集,指1971/1 ~ 2017/12的各月trend實際值
(2) 訓練後模型 = 模型.fit(disp=0)
(3) 預測2018/1 ~ 2019/8共20個月的trend值
trend預測值 = 訓練後模型.forecast(steps=20)
*steps參數是用來設定要預測的期數,此次練習是預測接續資料集最後一個月2017/12之後20個月2018/1~2019/8的數值
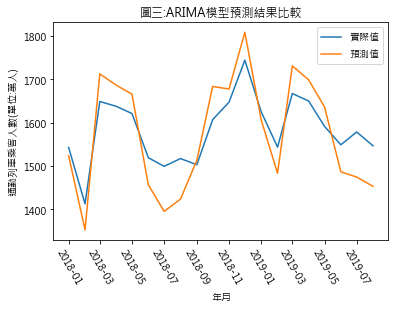
(4) 通勤列車乘客人數預測值 = trend預測值 + 對應各期的seasonality
圖三為預測結果.
(5) 模型預測效能
利用先前練習過的均方根方法(Root Mean Squared Error,RMSE)來檢驗ARIMA模型的預測效能,得出的RMSE高達64.3283,最這幾次練習中數值最差的,代表其效能最差.
得出此結果,並不是因ARIMA模型本質效能差,而是我們用錯誤資料集運用ARIMA模型.先前已提過AR或MA模型須在穩定性(stationary)資料集下操作.此例我們是用一階差分來調整資料集的穩定性,但在之前做AR模型練習時,我們已發現用一階差分的trend資料做ADF檢定,其結果
ADF Statics: -3.284412
p value: 0.015590
Critical Values:
1%: -3.442
5%: -2.867
10%: -2.570
p value雖 < 0.05,符合穩定性檢定,但ADF Statics之值仍不夠低.
另種可能性,是ARIMA導入MA模型後,模型複雜化後導致模型的自由度降低,而影響到效能.在先前利用trend對數的一階差分的AR模型練習中,最適遞延期數為18期,但在此次練習的ARIMA模型,套用在AR模型部份的遞延期數僅有10期.
(初稿於中華民國108年12月13號)
限會員,要發表迴響,請先登入








