Chap. 6 Free Electron
完全不受拘束的電子(滿足Pauli principle)
-
Heat capacity of metal
-
Electrical conductivity
-
Cyclotron
-
Hall effect
-
Thermal conductivity
電子貢獻,假設所有電子都有貢獻
U=3(kᴃT/2)N=3kᴃTN/2, CV= 3kᴃN/2=0.54 joul/gK
experimental value CV=1.23 joul/gK
phonon 貢獻 CV=3NkB=1.08 joul/gK
所以free electron貢獻 CV=1.23 – 1.08 = 0.15 joul/gK, 與0.54相差太多
Energy level of free electron gas:
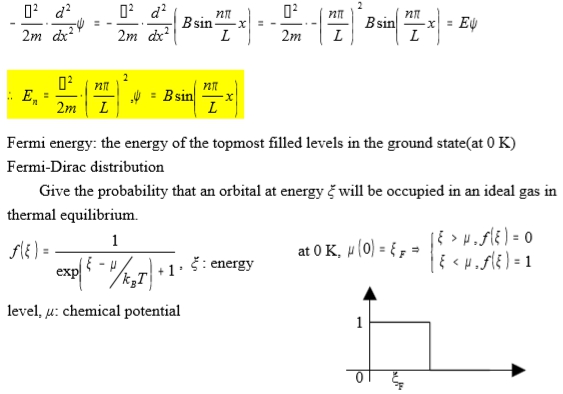
Consider a free electron in 1-D Hψ=Eψ, H=P²/2m=(-ℏ²/2m)∙d²/dx²
⸪ P=-jℏ=-jℏ∙d/dx, (-ℏ²/2m)∙d²ψ/dx²=Eψ boundary condition ψ(0)=ψ(L)=0
ψ=Acoscx+Bsincx, ψ(0)=0 → A=0, ψ(L)=0 → BsincL=0, cL=nπ ⸫c=nπ/L n=1,2,3,…
(-ℏ²/2m)∙d²ψ/dx²=(-ℏ²/2m)∙d²[Bsin(nπx/L)]/dx²=(-ℏ²/2m)∙-(nπ/L)²Bsin(nπx/L)=Eψ
⸫ Eₙ=ℏ²/2m∙(nπ/L)², ψ=Bsin(nπx/L)
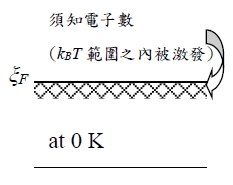
Fermi energy: the energy of the topmost filled levels in the ground state(at 0 K)
Fermi-Dirac distribution
Give the probability that an orbital at energy ξ will be occupied in an ideal gas in thermal equilibrium.
f(ξ)=1/[e(ξ-μ)/kᴃT+1], ξ : energy level, μ: chemical potential
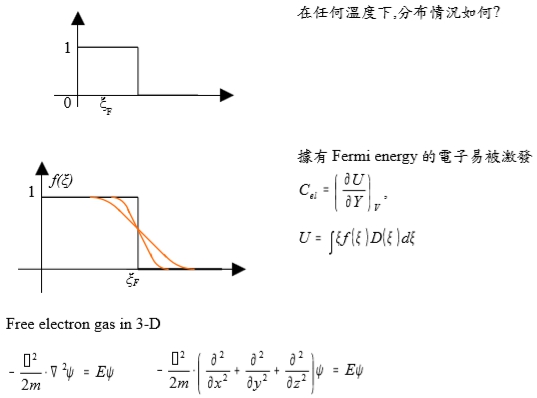
at 0 K, μ(0)=ξF, (i)ξ>μ, f(ξ)=0, (ii)ξ<μ, f(ξ)=1
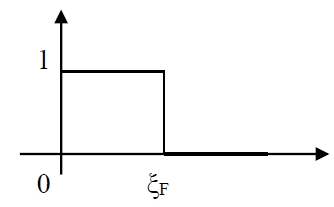
在任何溫度下,分布情況如何? 據有Fermi energy的電子易被激發
Cₑₗ=∂U∕∂T|ᵥ, U=∫ξf(ξ)D(ξ)dξ
Free electron gas in 3-D
(-ℏ²/2m)∙²ψ=Eψ → (-ℏ²/2m)∙(∂²∕∂x²+∂²∕∂y²+∂²∕∂z²)ψ=Eψ
ψ=Asin(nₓπx/L)sin(nyπy/L)sin(nzπz/L)
(-ℏ²/2m)∙²ψ=Eψ → ²ψ+(2mE/ℏ²)ψ=0 let k²= 2mE/ℏ², E=ℏ²k²/2m=P²/2m
²ψ+k²ψ=0 , ψ=Aexp(-jk∙r)
Heat capacity of metal
Total internal energy of free electron gas: U=∫₀∞ξf(ξ)D(ξ)dξ
Cₑₗ=∂U∕∂T|ᵥ=∫₀∞ξ(∂f(ξ)/∂T)D(ξ)dξ,
total N=∫₀∞f(ξ)D(ξ)dξ=const. → ∫₀∞(∂f(ξ)/∂T)D(ξ)dξ=0, 乘上ξF
ξF∫₀∞(∂f(ξ)/∂T)D(ξ)dξ=0 → Cₑₗ=∫₀∞(ξ-ξF)(∂f(ξ)/∂T)D(ξ)dξ
at low temperature, f(ξ)=const. → ∂f(ξ)/∂T=0
在靠近ξF 處之電子才有貢獻,使∂f(ξ)/∂T≠0,因此我們可以只算ξF 附近的D(ξF)的能階數
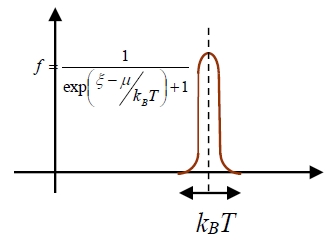
μ=μ(T) μ → ξF
Cₑₗ=∫₀∞(ξ-ξF)(∂f(ξ)/∂T)D(ξF)dξ=D(ξF)∫₀∞[(ξ-ξF)²/kᴃT²][e(ξ-μ)/kᴃT/(e(ξ-μ)/kᴃT+1)²]dξ
let x=(ξ-ξF)/kᴃT, Cₑₗ=D(ξF)kᴃ²T∫-ξf/kᴃT ∞[x²ex/(ex+1)²]dx=D(ξF)kᴃ²T∫-∞∞[x²ex/(ex+1)²]dx
i.e. ∫₀∞[x/(eax+1)]dx=π²/12a² → ∂∫₀∞[x/(eax+1)]dx∕∂a=∂(π²/12a²)/∂a
→ ∫₀∞[x²ex/(ex+1)²]dx=π²/6 (if a=1)
Density of state: D(ξ)=3N(ξ)/2ξ → D(ξF)=3N(ξ)/2ξF
∵Total number of orbitals, N=2[4πk³/3]/(2π/L)³=Vk³/3π² → kF=(3π²N/V)1/3 and ξF= ℏ²kF²/2m N=(V/3π²)( 2mξ/ℏ²)3/2 → D(ξ)= dN(ξ)/dξ=(V/2π²)( 2mξ/ℏ²)3/2ξ1/2
or 取對數再微分 → lnN=3lnξ/2+cost. → dN/N=3dξ/2ξ → dN/dξ=3N/2ξ=D(ξ)
Cₑₗ=D(ξF)kᴃ²T∫-∞ ∞[x²ex/(ex+1)²]dx=[3N(ξ)kᴃ²T/2ξF]∙(π²/3)=π²Nkᴃ²T/2ξF
Fermi temperature: TF=ξF/kᴃ → Cₑₗ=(π²Nkᴃ/2)∙(kᴃ/ξF)T=(π²Nkᴃ/2)∙(T/TF)
定性分析
N=(V/3π²)( 2mE/ℏ²)3/2, ∆N=N(ξF)-N(ξF-kᴃT)=(V/3π²)( 2mξ/ℏ²)3/2[1-(1-kᴃT/ξF)3/2]=(V/3π²)( 2mξ/ℏ²)3/2∙(3kᴃT/2ξF)=3NT/2TF
U=∆NkᴃT =3NkᴃT²/2TF → Cₑₗ=∂U∕∂T|ᵥ=3Nkᴃ(T/TF) T
金屬的比熱(at low temperature): C=Cₚₕₒₙₒₙ+Cₑₗ=AT³+rT → C/T=AT²+r
for conductor, T<TF, TD
Electrical conductivity σ=1/ρ, 電子運動的平均結果
The electrical resistivity is caused by,
-
The collisions of electrons with phonons
-
The collisions of electrons with lattice imperfections, impurity atoms,
經過l(mean free path)能夠通過某一截面的粒子數:
N=N₀e-x/l= N₀e-vt/vτ=N₀e-t/τ
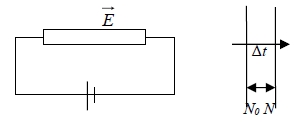
Number of electrons without suffering collisions during the time interval Δt
N₀e-∆t/τ=N₀(1-∆t/τ)
Number of electrons with collisions during the time interval Δt: N-N₀= N₀(∆t/τ)
P(t): the average momentum of an electron, P(t)─Δt→P(t+Δt)
P (t+Δt)=1/N₀{[N₀(1-∆t/τ)(P(t)+FΔt)]+[N₀(∆t/τ)FΔt]}=(1-∆t/τ)(P(t)+FΔt)]+(∆t/τ)FΔt
i.e. F(t)=const., P(t)=e-t/τP(0)+Fτ(1-e-t/τ)
the displacement of the Fermi sphere in the steady state(t>>) is given by:
P=Fτ=(-eE)τ, dP/dt=P/τ+F
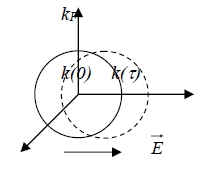
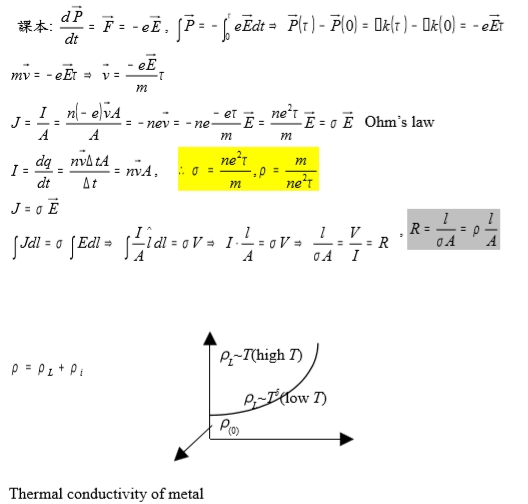
課本(C. Kittel): dP/dt=F=-eE, ∫P =-∫₀τeEdt → P(τ)-P(0)=ℏk(τ)-ℏk(0)=-eEτ
mv=-eEτ, v=-eEτ/m
J=I/A=N(-e)vA/A=-Nev=-Ne(-eEτ/m)=(Ne²τ/m)E=σE Ohm’s law
I=dq/dt=nv∆tA/∆t= nvA, ⸫ σ=Ne²τ/m, ρ=m/Ne²τ
J= σE → ∫Jdl=σ∫Edl → ∫Idl/A=σV → Il/A=σV → l/σA=V/I=R, R=l/σA=ρl/A
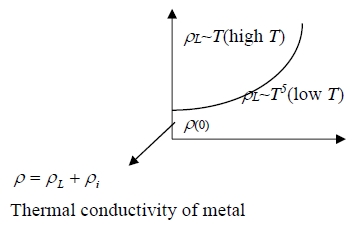
Thermal conductivity of metal k=Cᵥvl/3, k=kₚₕₒₙₒₙ+kₑₗ
kₑₗ=(π²Nkᴃ²T/2ξF)∙vFl/3=(π²Nkᴃ²τ/3m)T i.e. l=vFτ, ξF=mvF²/2
at room temperature: lph-ph≈lph-el , kₑₗ/kₚₕₒₙₒₙ=10 ⸪ kₑₗ值很大, metal導熱快
k=kel+kph
-
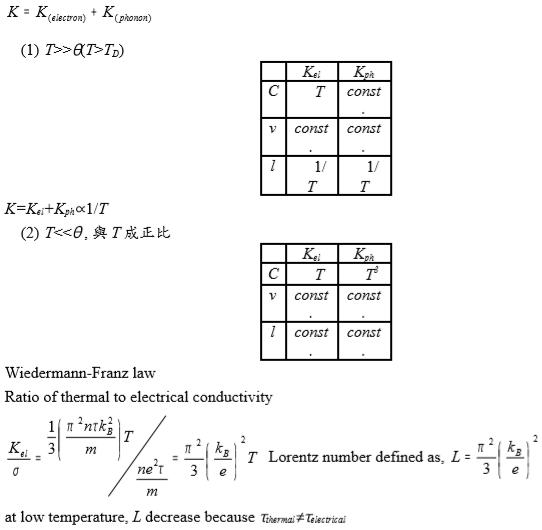
T>>(T>TD)
-
kel
kph
C
T
const
v
const
const
l
1/T
1/T
-
k=kel+kph 1/T
-
T<< , 與T成正比
-
kel
kph
C
T
T³
v
const
const
l
const
const
-
Wiedermann-Franz law
Ratio of thermal to electrical conductivity
kₑₗ/σ=[(π²Nkᴃ²τ/3m)T ]/(Ne²τ/m)=π²kᴃ²T/3e²
Lorentz number defined as, L=π²kᴃ²T/3e²
at low temperature, L decrease because thermalelectrical
註記: □=ℏ Planck constant

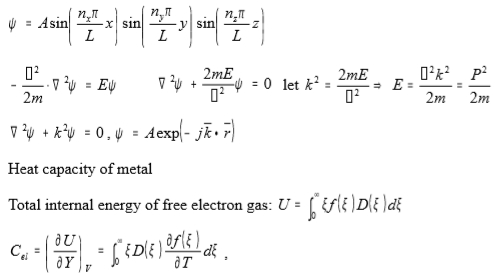

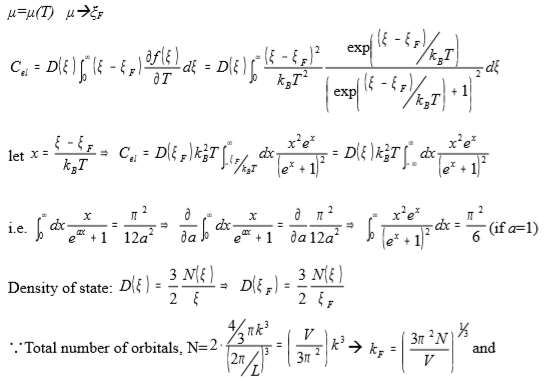



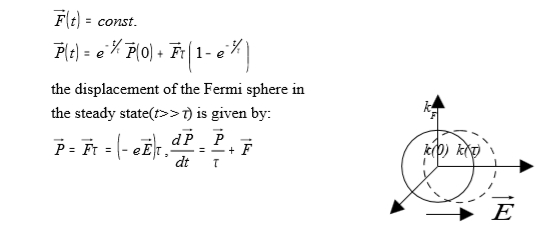
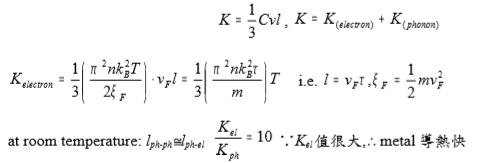
- 2樓. 宋坤祐2023/02/03 21:51
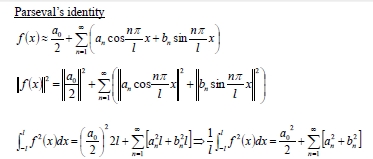
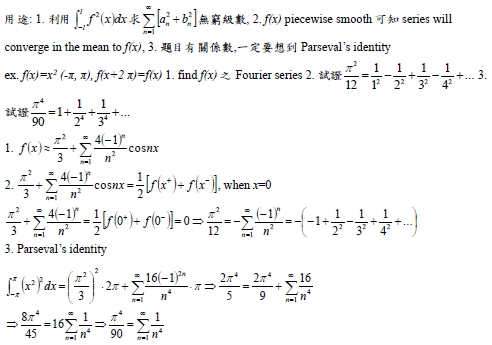
- 1樓. 宋坤祐2022/12/07 15:40