物化第一章 氣體的性質

氣體的基本量: 壓力, 溫度

  

熱力第零定律: A系統與B系統達成熱平衡,若C系統與B也達成熱平衡.那麼C也會與A達成熱平衡

氣體表示式: pV=nRT, p:壓力, V:體積, T:溫度, n:氣體質量, R:氣體常數

遵守氣體方程式的氣體稱為理想氣體,氣體方程式可視為狀態函數之一

Boyles law: V1/p, or pV=constant (for constant n, T), 當p→0時,氣體遵守此定律

分子的解釋基於氣體壓力來自粒子碰撞器壁產生的,當體積減半,粒子密度就倍增,因此碰撞次數也就倍增,氣體施力的平均值(壓力)也就倍增

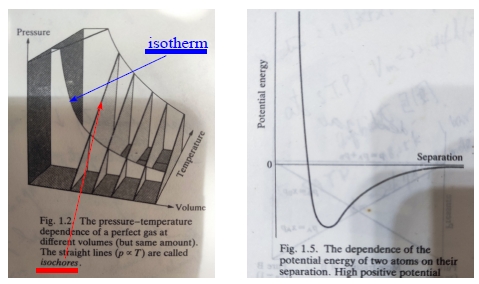
p_fV_f=p_iV_i (for constant n, T), 每一個溫度的pV曲線稱為isotherm等溫線, Fig. 1.2.

Gay-Lussacs law: VT (for constant n, p), p T (for constant n,V)

V_f=(T_f/T_i )V_i (for constant n, p), p_f=(T_f/T_i )p_i (for constant n,V)

真實氣體的不完美

分子間的相互作用: 中長距離時,分子有吸引力;距離非常接近時,分子間產生斥力,如U-r曲線所示, Fig.1.5.

真實氣體與理想氣體之間,可以壓縮因子Z來比較,因為pVₘ=RT, where Vₘ=V/n

Z=pVₘ/ RT, e.g. Z=1 for ideal gas

(i)在高壓時,所有氣體Z>1,比理想氣體更難壓縮,分子間的斥力在主導

(ii)at intermediate pressure, 有一些氣體Z<1, span="" style="font-family:標楷體 , cursive" data-mce-style="font-family: 標楷體 , cursive;">表示分子間的吸引力在主導,利於壓縮

真實氣體行為的分析: 真實氣體處於高溫和低密度的條件下, 其等溫線遵守pVₘ=RT,但從實驗的等溫線(Fig.1.7.)得知並不簡單,狀態方程式形式可為:

pVₘ=RT(1+Bp+Cp²+...) or pVₘ=RT(1+B/Vₘ+C/Vₘ²+...), virial係數: B,C,B,Cf(T)

Boyle 溫度,T_B: 當係數B=0, pVₘ≈RT其他Cp²和高次項太小可忽略不計

  

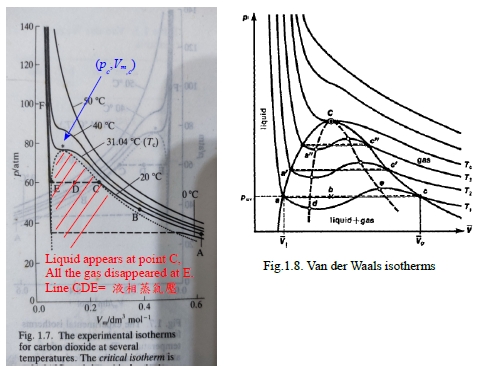
臨界常數, Tc pc Vₘc : Tc 等溫線上有一臨界點(pc,Vₘc),在Tc 以上的等溫線不會出現液相;而Tc以下的等溫線會有水平線(液相凝結)出現,臨界點(pc,Vₘc)即是水平線兩端互相重合的奇點

真實氣體方程式: 由於virial equation, pVₘ=RT(1+Bp+Cp²+...)太複雜,我們以van der Waals eq.作為近似真實氣體方程式的表示: (p+an²/V²)(V-nb)=nRT or p=RT/(Vₘ-b)-a/Vₘ²

(i)粒子的體積≠0, nb近似所有粒子的體積總和

(ii)粒子間的吸引力會減少氣體壓力,直接影響碰撞器壁的頻率和輕重,因此減少的壓力與粒子密度的平方成正比; ∆p(n/V)², ∆p稱為氣體的內壓, ∆p=a/Vₘ²

將van der Waals eq.展開: Vₘ³-(b+RT/p)Vₘ²+(a/p)Vₘ-ab/p=0, 如Fig.1.8.計算的等溫線

van der Waals氣體方程式p=RT/(Vₘ-b)-a/Vₘ²的特徵:

1. Tc以下的等溫線產生的震盪曲線不是實際的情形,實際的情形為一水平線

2. 理想氣體的等溫線是處於高溫和低密度的條件下,因為高溫, RT/(Vₘ-b)遠大於a/Vₘ², 低密度的條件可把Vₘ-b視為Vₘ,方程式即變為p=RT/Vₘ

3. T_c以下氣液相共存是因等號右邊的前後項大小接近,互相平衡的結果,RT/(Vₘ-b)代表粒子的動能和粒子間的斥力,a/Vₘ²則是粒子間的吸引力

4. 臨界溫度Tc以下的等溫線的震盪曲線會收斂於Tc的等溫線上的反曲點(pc,Vₘc),數學上該點的斜率和曲率均為零, 亦即dp/dVₘ=0, d²p/dVₘ²=0

dp/dVₘ=-RT/(Vₘ-b)²+2a/Vₘ³=0, d²p/dVₘ²=2RT/(Vₘ-b)³-6a/Vₘ⁴=0 →解Tc, pc,Vₘc
→ Vₘc=3b, Tc=8a/27Rb, pc=a/27b², Z=pcVₘc/RTc=3/8=0.375 vs. 實驗值約0.3

1. Boyle 溫度,T_B: 先將van der Waals eq.整理成pVₘ=RT(1+B/Vₘ+C/Vₘ²+...)的形式

p=RT/(Vₘ-b)-a/Vₘ² → p=RT/Vₘ[1/(1-b/Vₘ)-a/RTVₘ], if b/Vₘ<<1, 1="" 1-="" span="" style="font-family:times new roman , serif" data-mce-style="font-family: times new roman , serif;">b/Vₘ)=1+b/Vₘ+(b/Vₘ)²+...

→ p≈RT/Vₘ[1+b/Vₘ+(b/Vₘ)²+...-a/RTVₘ]=RT/Vₘ[1+(b-a/RT)/Vₘ+(b/Vₘ)²+...] ⸫ B=b-a/RT
當B=0時, b-a/RT=0, TB=a/Rb=27Tc/8

ex.1.8 pV=nRT=mRT/M → M=mRT/pV=ρ(RT/p),作圖ρ/p vs. p 外插至p→0的截距(ρ/p)ₚ→₀ M=RT(ρ/p)ₚ→₀=0.0820575298.151.8748=45.88

ex.1.31 barometric fomula p(h)=p₀e^-Mₘgh/RT , dp=-ρgdh ⸪pMₘ=ρRT → dp=-pMₘgdh/RT 積分∫ₚ_₀^ₚdp/p=∫₀^ₕ-Mₘgdh/RT → ln(p/p₀)=-Mₘgh/RT → p=p₀e^-Mₘgh/RTex.1.25 virial expansion at 273K, pVₘ/RT=1-(21.7cm³mol⁻¹/Vₘ)+(1200cm⁶mol⁻²/Vₘ²)+... 求critical constants? Virial coefficients: B=-21.7, C=1200p=RT/Vₘ[1+(b-a/RT)/Vₘ+(b/Vₘ)²+...], b-a/RT=-21.7, b²=1200 ⸫a=1261, b=C^½=34.64Vₘ_c=103.92cm³mol⁻¹, T_c=131.5K, p_c=3.89atm

第二章 第一定律概念

敘述1: 當一系統沿絕熱路徑由A狀態變至B狀態,無論任何方法它做的功都一樣; w_ad=U_f-U_i

p.s. 絕熱adiabatic: containers that do not permit energy to be transferred as heat, vs. diathermic.

若不是絕熱路徑,熱量heat是內能變化與做功的差值; q=∆U-w or q=w_ad-w

敘述2: 隔絕系統的能量是固定的; U=U₀, ⸪∆U=q+w & q=w=0

看成微小變化: dU=dq+dw, i.e. dw: work done on system, dq: heat supplied to system.

功: a. 機械功 b.收縮/膨脹功 c. 自由膨脹 d. 定壓膨脹 e. 可逆膨脹

a. 人(系統)對物體作功,由高度z_i移到z_f(z_f>z_i); dw=∫_zᵢ^zᶠ-F(z)dz=-(z_f-z_i)|F| F是重力,方向往下

b. 氣體對抗外部定壓力p_ex, 膨脹dV; dw=p_exdV

c. 當p_ex=0發生自由膨脹,dw=0

d. 膨脹過程中p_ex都是固定值, dw=-∫_Vᵢ^Vᶠp_exdV=-p_ex(V_f-V_i)=-p_ex∆V

e. 可逆過程: isothermal expansion of a perfect gas, dw=-∫_Vᵢ^Vᶠp_indV=-∫_Vᵢ^Vᶠ(nRT/V)dV=-nRTln(V_f/V_i)

 

熱: dTdq or dq=CdT, C: heat capacity; Cₘ=C/n

heat capacity: isochoric Cᵥ at dV=0 & dw=0; isobaric Cₚ at dp=0

1^st law: dU=dq+dw=dq+dwₑ-p_ex∆V,

when ∆V=0 and dwₑ=0 → dU=dq at constant volume, no other work. Implies Cᵥ=(∂U/∂T)ᵥ

 

ex. van der Waals eq. p=nRT/(V-nb)-an²/V²

(∂p/∂T)ᵥ=nR/(V-nb); (∂p/∂V)_T=-nRT/(V-nb)²+2an²/V³

∂²p/∂T∂V=-nR/(V-nb)²; ∂²p/∂V∂T=-nR/(V-nb)² ⸫ ∂²p/∂T∂V=∂²p/∂V∂T

 

ex. Dieterici eq. p={nRT/(V-nb)}exp(-an/RTV)

(∂p/∂T)ᵥ={nR/(V-nb)}exp(-an/RTV)+{nRT/(V-nb)}an/RT²Vexp(-an/RTV)

={nR/(V-nb)}exp(-an/RTV)[1+an/RTV]

(∂p/∂V)_T={-nRT/(V-nb)²}exp(-an/RTV)+{nRT/(V-nb)}an/RTV²exp(-an/RTV)={nRT/(V-nb)}exp(-an/RTV)[-1/(V-nb)+an/RTV²]

∂²p/∂T∂V={-nR/(V-nb)²}exp(-an/RTV)[1+an/RTV]+{nRT/(V-nb)}an/RTV²exp(-an/RTV)[1+an/RTV]+{nR/(V-nb)}exp(-an/RTV)(-an/RTV²)={nR/(V-nb)}exp(-an/RTV){-1/(V-nb)[1+an/RTV]+an/RTV²[1+an/RTV]-an/RTV²}={nR/(V-nb)}exp(-an/RTV){1/(V-nb)[1+an/RTV]+(an/RT)²V³]

∂²p/∂V∂T={nR/(V-nb)}exp(-an/RTV)[-1/(V-nb)+an/RTV²]+{nRT/(V-nb)}an/RT²V exp(-an/RTV)[-1/(V-nb)+an/RTV²]+{nRT/(V-nb)}exp(-an/RTV)[-an/RT²V²]={nR/(V-nb)}exp(-an/RTV){-1/(V-nb)+an/RTV²+an/RTV[-1/(V-nb)+an/RTV²]-an/RTV²}={nR/(V-nb)}exp(-an/RTV){-1/(V-nb)[1+an/RTV]+(an/RT)²V³} ⸫ ∂²p/∂T∂V=∂²p/∂V∂T

 

 

Cₚ是甚麼? 先定義H=U+pV, 為了確認dH=(dq)ₚ, 考慮微小變化H+dH=(U+dU)+(p+dp)(V+dV)

→ H+dH=U+pV+dU+Vdp+pdV+dpdV i.e. dpdV太小可忽略

H=U+pV的微分dH=dU+d(pV)=dU+Vdp+pdV, 前面有提到dU=dq+dw=dq+dwₑ-p_ex∆V 代入

dH= dq+dwₑ+Vdp it means dH= dq at constant volume, no other work. Implies Cₚ=(∂U/∂T)ₚ

H焓在定壓的過程扮演能量傳遞的重要角色,焓與內能的差別是由於系統體積改變產生的功

H=U+pV=U+nRT (ideal gas)→ dH=dU+nRdT ⸪ dU=CᵥdT, dH=CₚdT ⸫ Cₚ-Cᵥ=nR

 

 

第三章 第一定律機構

狀態函數與其微分

一般性質的分類依照尺寸大小, extensive性質會與其大小有關, ex. m, q, C_v, V; intensive性質則與尺寸無關, ex. T, ρ, p, Vₘ.

熱力學區分函數有兩種: 狀態函數和路徑函數, 譬如內能和溫度屬狀態函數, 跟其系統的現狀有關,與其前後過程無關;反之,熱與功的多少則與其過程有關,屬於路徑函數

ex. Uᵢ(pᵢ,Vᵢ,Tᵢ)→U_f(p_f,V_f,T_f), 從Uᵢ 狀態到U_f 狀態,可由adiabatic或non-adiabatic路徑完成,其中變化的q和w就不同, i.e. U_f-Uᵢ=∆U=∫ᵢ^ᶠdU vs. q=∫ᵢ^ᶠ_ₚₐₜₕdq≠q_f-qᵢ

 

 

狀態函數的數學特性: 若經過一封閉迴路的過程, 其狀態變化為零, 即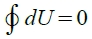

; 同時與積分路徑無關,也符合exact differential的特性

df=gdx+hdy is exact if (∂g/∂y)ₓ=(∂h/∂x)_y If df is exact, then its inegral between specified limits is independent of the path.

內能變化: U=U(V,T) U可視為(p,V,T)的函數, p 可以V 和T 表示,所以方便起見,內能U為V 和T 的函數,因此內能變化dU=U(V+dV,T+dT)-U(V,T)=(∂U/∂V)_TdV+(∂U/∂T)_VdT

偏導數關係: f(x,y), df=(∂f/∂x)_ydx+(∂f/∂y)ₓdy and ∂²f/∂x∂y=∂²f/∂y∂x

when z=z(x,y), like p=p(V,T)

relation 1: when x changed at fixed z, (∂f/∂x)_z=(∂f/∂x)_y+(∂f/∂y)ₓ(∂y/∂x)_z

relation 2: (∂x/∂y)_z=1/(∂y/∂x)_z

relation 3: (∂x/∂y)_z=-(∂x/∂z)_y(∂z/∂y)ₓ → (∂x/∂y)_z(∂y/∂z)ₓ(∂z/∂x)_y=-1 Euler chain relation

pf: f(x,y,z)=0, x(y,z) & z(x,y) → dx=(∂x/∂y)_zdy+(∂x/∂z)_ydz...(a), dz=(∂z/∂x)_ydx+(∂z/∂y)_xdy...(b)代入(a)

→ dx=(∂x/∂y)_zdy+(∂x/∂z)_y[(∂z/∂x)_ydx+(∂z/∂y)_xdy]=dx+[(∂x/∂y)_z+(∂x/∂z)_y(∂z/∂y)_x]dy

⸫ (∂x/∂y)_z+(∂x/∂z)_y(∂z/∂y)_x=0, (∂x/∂y)_z=-(∂x/∂z)_y(∂z/∂y)ₓ

第一定律: dU=dq+dw, dw=dwₑ-p_ex∆V or dU=(∂U/∂V)_TdV+(∂U/∂T)_VdT

H=U+pV, H=H(p,T) → dH=(∂H/∂p)_Tdp+(∂H/∂T)_pdT

將Cᵥ=(∂U/∂T)ᵥ, Cₚ=(∂U/∂T)ₚ 代入, dU=CᵥdT+(∂U/∂V)_TdV, dH=CₚdT+(∂H/∂p)_Tdp

內能的溫度關係: dU=CᵥdT+(∂U/∂V)_TdV → (∂U/∂T)ₚ=Cᵥ+(∂U/∂V)_T(∂V/∂T)ₚ

定義等壓熱膨脹係數, α=(1/V)(∂V/∂T)ₚ ⸫ (∂U/∂T)ₚ=Cᵥ+αV(∂U/∂V)_T

what is (∂U/∂V)_T? 材料在等溫壓縮時,粒子間的交互作用增加,此交互作用貢獻到系統的內能,猶如van der Waals氣體的a/Vₘ².

pf: dU=TdS-pdV → (∂U/∂V)_T=T(∂S/∂V)_T-p=T(∂p/∂T)ᵥ-p

(i) ideal gases obey pV=nRT → (∂p/∂T)ᵥ=nR/V, ⸫ (∂U/∂V)_T=T(∂p/∂T)ᵥ-p=nRT/V-p=0

(ii) van der Waals gas: p=nRT/(V-nb)-an²/V² → (∂p/∂T)ᵥ=nR/(V-nb)

⸫ (∂U/∂V)_T=T(∂p/∂T)ᵥ-p=nRT/(V-nb)-p=an²/V²=a/Vₘ²

 

焓的溫度關係: dH=CₚdT+(∂H/∂p)_Tdp → (∂H/∂T)ᵥ=Cₚ+(∂H/∂p)_T(∂p/∂T)ᵥ

由relation 3得, (∂p/∂T)ᵥ=-(∂V/∂T)ₚ/(∂V/∂p)_T=-αV/(∂V/∂p)_T

定義等溫壓縮係數, κ=-(1/V)(∂V/∂p)_T ⸫ (∂H/∂T)ᵥ=Cₚ+(α/κ)(∂H/∂p)_T

(∂H/∂p)_T也可由Euler chain relation得,

(∂H/∂p)_T=-1/(∂p/∂T)_H(∂T/∂H)ₚ=-(∂T/∂p)_H(∂H/∂T)ₚ=-(∂T/∂p)_HCₚ → (∂H/∂T)ᵥ=Cₚ-(αCₚ/κ)(∂T/∂p)_H

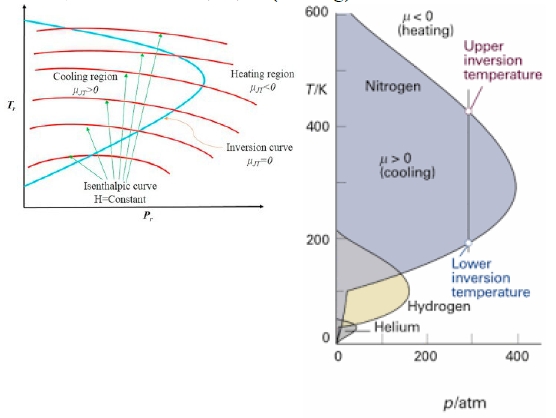
what is (∂T/∂p)_H? 定義Joule-Thomson係數, μ_JT=(∂T/∂p)_H, 也稱Joule-Thomson effect

 

 

→ (∂H/∂p)_T=-μ_JTCₚ, and (∂H/∂T)ᵥ=Cₚ-(αCₚ/κ)(∂T/∂p)_H=Cₚ(1-αμ_JT/κ)

μ_JT的意義:

dH=(∂H/∂p)_Tdp+(∂H/∂T)_pdT=CₚdT+(∂H/∂p)_Tdp, as dH=0, (dT/dp)_H=-(∂H/∂p)_T/Cₚ

dH=TdS+Vdp → (∂H/∂p)_T=T(∂S/∂p)_T+V=-T(∂V/∂T)_p+V 代入上式

→ (∂T/∂p)_H=[T(∂V/∂T)_p-V]/Cₚ

(i) ideal gases obey pV=nRT → (∂V/∂T)_p=nR/p, ⸫ μ_JT=(∂T/∂p)_H=[nRT/p-V]/Cₚ=0

(ii) van der Waals gas: p=RT/(Vₘ-b)-a/Vₘ² → Vₘ=RT/p+b-a/pVₘ+ab/pVₘ² 因為最後二項的值太小可忽略不計,為簡化計算方便故,將Vₘ以RT/p取代: Vₘ=RT/p+b-a/RT+ abp/R²T²

(∂Vₘ/∂T)_p=R/p+a/RT²-2abp/R²T³, T(∂Vₘ/∂T)_p=RT/p+a/RT-2abp/R²T²,

T(∂Vₘ/∂T)_p-Vₘ=RT/p+a/RT-2abp/R²T²-(RT/p+b-a/RT+ abp/R²T²)=-b+2a/RT-3abp/R²T²

μ_JT=(∂T/∂p)_H=[T(∂Vₘ/∂T)_p-Vₘ]/Cₚ=(-b+2a/RT-3abp/R²T²)/Cₚ, At low pressure and high temperature 3abp/R²T² term is very small, μ_JT≈(2a/RT-b)/Cₚ

μ_JT的正負大小取決於(2a/RT-b), 記住∂p<0 span="">

(i)當2a/RT>b, μ_JT>0, 所以∂T<0, span="">氣體在降溫(cooling) → 液化氣體

(ii)當2a/RT=b, μ_JT=0, Tᵢₙᵥ=2a/Rb=2T_B

(iii)當2a/RT_JT<0, span="">所以∂T>0, 氣體在升溫(heating)

 

Cᵥ與Cₚ的關係:

Cₚ-Cᵥ=(∂H/∂T)ₚ-(∂U/∂T)ᵥ=(∂U/∂T)ₚ+(∂pV/∂T)ₚ-(∂U/∂T)ᵥ=(∂U/∂T)ₚ-(∂U/∂T)ᵥ+p(∂V/∂T)ₚ

i.e. dU=(∂U/∂V)_TdV+(∂U/∂T)_VdT→(∂U/∂T)ₚ=(∂U/∂V)_T(∂V/∂T)ₚ+(∂U/∂T)_V 代入上式

Cₚ-Cᵥ=(∂U/∂V)_T(∂V/∂T)ₚ+p(∂V/∂T)ₚ=αV[(∂U/∂V)_T+p] ⸪α=(1/V)(∂V/∂T)ₚ

dU=TdS-pdV → (∂U/∂V)_T=T(∂S/∂V)_T-p=T(∂p/∂T)ᵥ-p 代入上式 Cₚ-Cᵥ= αVT(∂p/∂T)ᵥ

(∂p/∂T)ᵥ=-(∂V/∂T)ₚ/(∂V/∂p)_T=α/κ, Cₚ-Cᵥ=(α²/κ)VT 固液相時, α很小可能Cₚ≈Cᵥ, 但κ也很小時 α²/κ會變大,必須回到Cₚ-Cᵥ=αV[(∂U/∂V)_T+p],α也許很小,但[(∂U/∂V)_T+p]可能很大!

理想氣體的α與κ: idal gas eq. pV=nRT

α=(1/V)(∂V/∂T)ₚ=(1/V)(nR/p)=1/T, κ=-(1/V)(∂V/∂p)_T =-(1/V)(-nRT/p²)=(1/p)(nRT/pV)=1/p

Cₚ-Cᵥ=(α²/κ)VT=pVT/T²=nR

絕熱膨脹功 w=-∫ᵢ^ᶠpdV

有時功或熱無法直接得到,可找一有關的狀態函數取最方便的路徑來計算其中的變化

w=∫ᵢ^ᶠdU=∫ᵢ^ᶠCᵥdT 因為(∂U/∂V)_T=0 for ideal gas. → w=Cᵥ(T_f-T_i)=Cᵥ∆T

系統做的功=內能降低的變化量, 反映在溫度下降

不可逆條件: ( i) no pₑₓ as expansion, → w=0, ∆T=0 (ii) at fixed pₑₓ, → w=-pₑₓ∆V=Cᵥ∆T, ⸫∆T=-pₑₓ∆V/Cᵥ

可逆條件: 內外壓力p都遵守ideal gas pV=nRT行為, dU=-pdV=CᵥdT

→ CᵥdT=-nRTdV/V, Cᵥ視為與溫度無關, → CᵥdT/T=-nRdV/V 積分

Cᵥ∫ᵢ^ᶠdT/T=-nR∫ᵢ^ᶠdV/V → Cᵥln(T_f/T_i)=-nRln(V_f/V_i) i.e. define c=Cᵥ/nR ⸫ ln(T_f/T_i)^c=ln(V_i/V_f)

T_f=(V_i/V_f)^1/c T_i → w=Cᵥ∆T=Cᵥ(T_f-T_i)=Cᵥ[(V_i/V_f)^1/c-1]T_i

def: γ=Cₚ/Cᵥ and Cₚ-Cᵥ=nR → c=Cᵥ/(Cₚ-Cᵥ), 1/c=γ-1, w=Cᵥ[(V_i/V_f)^γ-1-1]T_i

⸪ p_iV_i/p_fV_f =T_i/T_f=(V_f/V_i)^γ-1 → p_iV_i^γ =p_fV_f^γ

V_i/V_f=(p_f/p_i)^1/γ → w=Cᵥ[(p_f/p_i)^{(γ-1) /γ}-1]T_i