第21章 統計熱力學概念
一系統有N個粒子,總能可求但能量分佈難以限定,因為粒子碰撞造成能量再分佈永無止息,可得最接近的能量分佈描述: 粒子擁有各自允許能量的平均數, ex. nᵢ個粒子在εᵢ能態上;目的是計算在任何溫度,各種運動的粒子類型的數量,好比{n₀,n₁,n₂,...}此集合就是系統的佈局(configuration).

佈局組合數目: 上圖二例: {N,0,0,...,0}只有一種方法;{N-2,2,0,...,0}有=½N(N-1)種方法
推廣至一般化佈局{n₀,n₁,n₂,...,nᵢ},其組合方法數目W=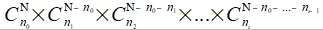
W=[N!/n₀!(N-n₀)!][(N-n₀)!/n₁!(N-n₀-n₁)!][(N-n₀-n₁)!/n₂!(N-n₀-n₁-n₂)!]...[(N-n₀-...-nᵢ₋₁)!/nᵢ!(N-n₀-...-nᵢ)!]=N!/[n₀!n₁!n₂!...nᵢ!(N-n₀-...-nᵢ)!]=N!/[n₀!n₁!n₂!...nᵢ!] (21.1)
i.e. N=∑ᵢnᵢ=n₀+n₁+n₂+...+nᵢ, and 0!=1
目標: 找出最可能出現的佈局方法數, W*;亦即{n₀*,n₁*,n₂*,...,nᵢ*}集合可以得到W*最大值
同時滿足兩個條件: N=∑ᵢnᵢ (21.2), E=∑ᵢnᵢεᵢ (21.3)
當W*=Wₘₐₓ時, dW=0; 所以當lnW*=lnWₘₐₓ時, d(lnW)=0 → d(lnW)=∑ᵢ(∂lnW/∂nᵢ)dnᵢ=0 (21.4)
利用Lagrange待定係數法求解,結合(21.2)(21.3)(21.4): dN=∑ᵢdnᵢ=0, dE=∑ᵢεᵢdnᵢ=0
d(lnW)=∑ᵢ(∂lnW/∂nᵢ)dnᵢ+α∑ᵢdnᵢ-β∑ᵢεᵢdnᵢ=0; α, β為常數, ∑ᵢ(∂lnW/∂nᵢ+α-βεᵢ)dnᵢ=0
→ ∂lnW/∂nᵢ+α-βεᵢ=0 (21.5)
lnW=ln{N!/[n₀!n₁!n₂!...nᵢ!]}=lnN!-ln[n₀!n₁!n₂!...nᵢ!]=lnN!-(lnn₀!+lnn₁!+...+lnnᵢ!)=lnN!-∑ᵢlnnᵢ!
≈NlnN-N-∑ᵢ(nᵢlnnᵢ-nᵢ)=NlnN-∑ᵢnᵢlnnᵢ (21.6)
∂lnW/∂nᵢ=-∑j[∂(njlnnj)/∂nᵢ]=-∑j[(∂nj/∂nᵢ)lnnj+nj(∂lnnj/∂nᵢ)], when j≠i, ∂nj/∂nᵢ=0
⸫ ∂lnW/∂nᵢ=-(lnnᵢ+1)≈-lnnᵢ i.e. nᵢ>>1
當nᵢ=nᵢ*, -lnnᵢ*+α-βεᵢ=0, nᵢ*=e(α-βεᵢ), 在εᵢ能態上的粒子數
N=∑jnj*=∑jeαe-βεʲ →eα=N/∑je-βεʲ then nᵢ*=eαe-βεʲ=N(e-βεʲ/∑je-βεʲ); β=1/kᴮT (21.7)
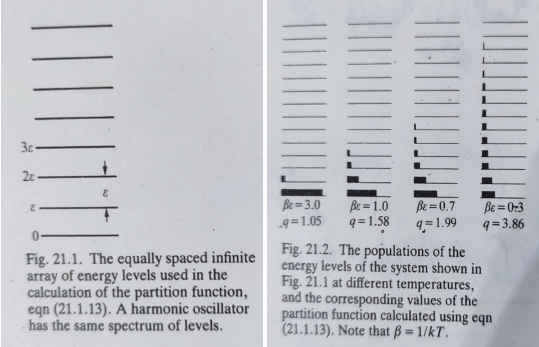
def: q≡∑je-βεʲ; β=1/kᴮT molecular partition function分子配分函數(統計熱力的核心),q包含系統中所有粒子的熱力資訊, ex. 雙原子分子的振動能階, fig.21.1
q=∑je-βεʲ=1+e-βε+e-2βε+e-3βε+...=1+e-βε+(e-βε)²+(e-βε)³+...=1/(1-e-βε)
p.s. 利用幾何級數a+ar+ar²+...+arn-1=a(1-rn)/(1-r)≈a/(1-r) if r<1, n="" font="">→∞
另類表示: q=∑jgje-βεʲ; gj: 簡併能階數, εj: 能態
Boltzmann分佈: 表示佔據εj的粒子數比率, nᵢ*/N=e-βεʲ/∑je-βεʲ=e-βεʲ/q=e-βεʲ(1-e-βε) (21.8)
求系統總能E=∑ᵢnᵢεᵢ, E=∑ᵢnᵢ*εᵢ=(N/q)∑ᵢεᵢe-βεᵢ=(N/q)∑ᵢ(-de-βεᵢ/dβ)=-(N/q)[d(∑ᵢe-βεᵢ)/dβ]=-(N/q)[dq/dβ]
E=-(N/q)[dq/dβ] → (E/N)q=-dq/dβ → εq=-dq/dβ, i.e. E/N=ε粒子的平均能量
若與時變Schrӧdinger eq. Hψ=(-ℏ/i)(∂ψ/∂t)對比, q等同波函數ψ; β=it/ℏ, 溫度倒數β如同虛數時間operator.
E=-(N/q)[∂q/∂β]的解釋: E可視為內能,假設基態ε₀和U(T=0)作為參考點:
U=U(0)+E, U-U(0)=-(N/q)[∂q/∂β]V=-N(∂lnq/∂β)V (21.9)
配分函數q就是一個連結,把內能(宏觀量)與各個粒子的能態(微觀量)綁在一起,其他的熱力函數都可經由q計算得到,因此配分函數q扮演熱波函數的角色,恰如量子力學中的波函數ψ.
E=kᴮT2(∂lnq/∂T)V;N (21.10) 同(21.9)
S=kᴮT(∂lnq/∂T)V;N +kᴮln Z (21.11)
A=-kᴮTlnq (21.12)
p=kᴮT(∂lnq/∂V)T;N (21.13)
μ=-NAkᴮT(∂lnq/∂N )T;V (21.14) NA:Avogadro number
配分函數q的定性詮釋, q=∑jgje-βεʲ; β=1/kᴮT
(i)當T→0, e-βεʲ→0 let q=g₀ 基態簡併數, (ii)當T→∞, e-βεʲ→1, q=g₀+g₁+g₂+...→∞
表示溫度為零,只有基態g₀ 可用;若溫度非常高,所有能態幾乎都可利用, fig.21.2
利用平移能為例計算配分函數q,在一容器有單原子理想氣體,容器體積V(V=XYZ, X是x方向的長度,以此類推),前面定義q=∑je-βεj, εj是粒子的平移能,εj=εj₍ₓ₎+εj₍y₎+εj₍z₎
q=∑jexp{-βεj₍ₓ₎-βεj₍y₎-βεj₍z₎}={∑jexp(-βεj₍ₓ₎)}{∑jexp(-βεj₍y₎)}{∑jexp(-βεj₍z₎)}=qXqYqZ
由一維薛丁格方程式可得原子能階εₙ=n²h²/8mX², n=1,2,3...
最低能階=h²/8mX², 其餘能階的相對能量=(n²-1)h²/8mX²,代入qX中的εj₍ₓ₎
qX=∑₁∞exp[-β(n²-1)h²/8mX²] 相對於體積,能階非常緊密可視為連續,用積分式替代
qX=∫₁∞exp[-β(n²-1)h²/8mX²]dn 為方便容許可忽略的誤差,將下限延伸為0, n²-1以n²取代
qX=∫₀∞exp[-βn²h²/8mX²]dn let t²=βn²h²/8mX², dn=(8mX²/h²β)½dt
qX=(8mX²/h²β)½∫₀∞e-t²dt=(8mX²/h²β)½(π½ /2)=(2πmX²/h²β)½, qY和qZ以此類推...
q=qXqYqZ=(2πmX²/h²β)½(2πmY²/h²β)½(2πmZ²/h²β)½=(2πm/h²β)3/2V=V/Λ³ (21.15), Λ=h(β/2πm)½
可以將(21.15)代入(21.9), U-U(0)=-(N/q)[∂q/∂β]V=-N(-3V/2βΛ³)/(V/Λ³)=3N/2β=3NkᴮT/2
i.e. [∂q/∂β]V=(dΛ⁻³/dβ)V=-(3V/Λ⁴)(dΛ/dβ)=(-3V/2βΛ³), dΛ/dβ=Λ/2β
正則系綜 canonical ensemble: 假想一系統有指定的體積、成份和溫度(N,V,T),然後複製N次,彼此保持相同溫度的接觸,可以互相交換能量,如此重複的想像組合稱為正則系綜. 其總能E是一常數,由於是複製,ℕ 可以趨向∞
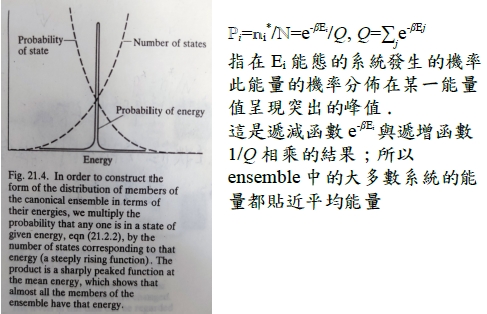
為何要引進正則系綜? 一是實際系統與周圍環境永遠在變化,狀態(能態)不斷的在變,牽涉到時間難以計算;ensemble以大數(ℕ→∞)取代時間的變數,第二個概念是先驗概率相等原則:任何能量分佈的機率都是平等的
主宰佈局dominating configuration: 正如前面描述系統中的粒子能態分佈的佈局,有一最大可能的配置和W* ;所以ensemble的總能E在ℕ個重複的系統也有一主宰佈局{n₀*,n₁*,...}和W*
W=ℕ!/n₀!n₁!... 為了求W*,ensemble同樣有2個限制條件: E=∑ᵢnᵢEᵢ, ℕ=∑ᵢnᵢ
按照之前過程,可得canonical分佈: nᵢ*/ℕ=e-βEᵢ/Q (21.16), Q=∑je-βEj (canonical partition function)
內能, U-U(0)=E/ℕ=(1/ℕ)∑ᵢnᵢEᵢ=(1/ℕ)∑ᵢ(ℕe-βEᵢ/Q)Eᵢ=(1/Q)∑ᵢe-βEᵢ Eᵢ=-(∂lnQ/∂β)ᵥ
當系統的組成粒子互不相關,因系統能量Ej是組成粒子的能量總和: Ej=εj⁽¹⁾+εj⁽²⁾+...+εj⁽ᴺ⁾ 代入Q
Q=∑jexp{-β(εj⁽¹⁾+εj⁽²⁾+...+εj⁽ᴺ⁾)}={∑je-βεj⁽¹⁾}{∑je-βεj⁽²⁾}...{∑je-βεj⁽ᴺ⁾} 如果粒子相同
Q={∑je-βεj}{∑je-βεj}...{∑je-βεj}={∑je-βεj}ᴺ=qᴺ 但是粒子相同且自由運動時,相同的能量有不同的組合, ex. E=εₐ+εᵇ+εᶜ(3個粒子a,b,c有3!種組合),因此在粒子無法分辨的情況下,會高估系統能量的組合數目,除了極低溫外,需呈上修正因子1/N!
⸫ Q=qᴺ/N! (粒子無法分辨); Q=qᴺ (粒子可分辨)
可不可分辨如何判斷? 原則(i)粒子是否同種類 (ii)處境,例如相同粒子在晶格中或在氣態中,晶格中有座標可追蹤,氣體分子自由運動無法追蹤
熱、功與熵:
U-U(0)=(1/ℕ)∑ᵢnᵢ*Eᵢ, ℕ→∞從公式觀察,內能變化來自於能態(Eᵢ→Eᵢ+dEᵢ)或數目(nᵢ*→nᵢ*+dnᵢ*)的變化: dU=dU(0)+(1/ℕ)∑ᵢnᵢ*dEᵢ+(1/ℕ)∑ᵢEᵢdnᵢ (21.17)
若是可逆變化,熱力學表示式: dU=dqᵣₑᵥ+dwᵣₑᵥ=TdS+dwᵣₑᵥ (21.18)
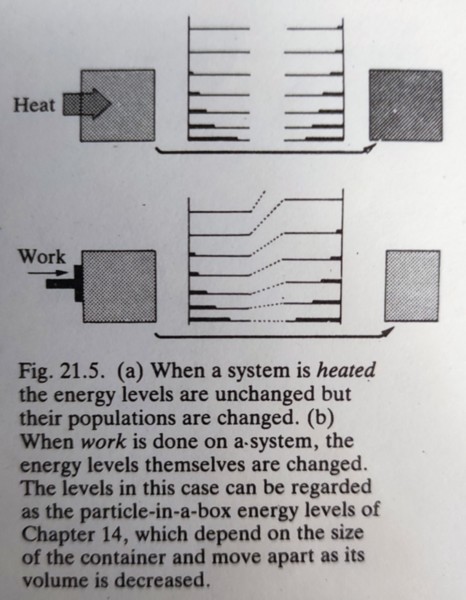
比較(21.16)和(21.17),可以建立連結: (i)當做功膨脹或壓縮,改變系統的大小,會改變系統的能階 (ii)系統被加熱或放熱,能階不變,但能態的數目會重新分佈. 照此可用熱與功做分類:
dqᵣₑᵥ=TdS=(1/ℕ)∑ᵢEᵢdnᵢ, dwᵣₑᵥ=dU(0)+(1/ℕ)∑ᵢnᵢ*dEᵢ. → dS=(1/ℕT)∑ᵢEᵢdnᵢ (21.19),
if entropy defined as S=(k/N)lnW*, ℕ→∞ i.e. W*: ensemble的最可能佈局的組合數
dS=(kв/ℕ)dlnW*=(kв/ℕ)∑ᵢ(∂lnW*/∂nᵢ)dnᵢ, 同時滿足(∂lnW*/∂nᵢ)+α-βEᵢ=0, 代入前式
dS=(kв/ℕ)∑ᵢ(-α+βEᵢ)dnᵢ=(kвβ/ℕ)∑ᵢEᵢdnᵢ (21.20), ⸪ ∑ᵢdnᵢ=0, 且同樣因熱造成改變,所以等同(21.19), 由此也可得β=1/kвT的關係
熱力3rd law: 完美晶體的熵,在溫度趨近於零時,會接近相同的值
當溫度下降,W*也會減少,是因為符合總能的佈局組合數目變少;在T=0極限情況下,W*=1使得lnW*=0,因為只有一種在最低能階的佈局才符合E=0,所以S→0,當T→0.
熵與配分函數: 熵的表示式可以配分函數有關的有用形式表達
S=(kв/ℕ)ln(ℕ!/n₀*!n₁*!...)=(kв/ℕ){lnℕ!-∑ᵢlnnᵢ*!}=(kв/ℕ){ℕlnℕ-ℕ-∑ᵢnᵢ*lnnᵢ*+∑ᵢnᵢ*}
=(kв/ℕ){ℕlnℕ-∑ᵢnᵢ*lnnᵢ*}=(kв/ℕ){∑ᵢnᵢ*lnℕ-∑ᵢnᵢ*lnnᵢ*}=kв∑ᵢnᵢ*/ℕ(lnℕ-lnnᵢ*)=-kв∑ᵢ(nᵢ*/ℕ)ln(nᵢ*/ℕ),
⸪ ℙᵢ=nᵢ*/ℕ=e-βEᵢ/Q (21.16), ⸫ S=-kв∑ᵢℙᵢlnℙᵢ=-kв∑ᵢℙᵢ(-βEᵢ-lnQ), i.e. lnℙᵢ=-βEᵢ-lnQ
S=kвβ∑ᵢℙᵢEᵢ+kв∑ᵢℙᵢlnQ=kвβ[U-U(0)]+kвlnQ, ∑ᵢℙᵢ=1, and ∑ᵢℙᵢEᵢ=∑ᵢnᵢ*Eᵢ/ℕ=U-U(0) (21.17)
→ S=[U-U(0)]/T+kвlnQ (21.22)
ex. the entropy of a monatomic gas, Q=qᴺ/N!
S=[U-U(0)]/T+kв(Nlnq-lnN!)=[U-U(0)]/T+nRlnq-kв(NlnN-N), since N=nNᴀ and R=kвNᴀ
S=[U-U(0)]/T+nR(lnq-lnN+1), in the case of a gas of monatomic particles, the only motion is translation, so q=V/Λ³ (21.15) and U-U(0)=3N/2β=3nRT/2
S=(3nRT/2)/T+nR(ln(V/Λ³)-lnnNᴀ +1)=nR[lne3/2+ln(V/Λ³)-lnnNᴀ +lne]=nRln(e5/2V/nNᴀΛ³)
⸫ S=nRln(aV), a= e5/2/nNᴀΛ³ and Λ=h(β/2πm)½ Sackur-Terrode eq. (21.23)
or alternative form S=nRln(e5/2kвT/pΛ³) for ideal gas, V=nRT/p
ex. entropy change in isothermal expansion for a perfect gas.
∆S=nRln(aVf)-nRln(aVi)=nRln(Vf/Vi), 結果與古典熱力學相同
統計熱力的核心是配分函數partition function, Q, 它介於熱力學、光譜學和量子力學之間,一旦知道Q,熱力學函數都可計算,如何計算Q?
若系統的粒子不可分辨時,已知Q=qN/N! and q=∑je-βεj, β=1/kвT
首先粒子的能量εj來自不同運動的貢獻, εj=εtranslation+εrotation+εvibration+εelectronic, 此種分別只是近似.
q=∑jexp(-βεᵀ-βεᴿ-βεV-βεᴱ)=[∑je-βεᵀ][∑je-βεᴿ][∑je-βεᴠ][∑je-βεᴱ]=qᵀqᴿqVqᴱ 個別運動的配分函數q, 其中的能態分佈牽涉粒子的能階情況,在量子力學裡討論,不在這長篇大論!
如何計算熱力學函數?
出發點由前面已得的內能U,和熵S的(21.17)(21.22)開始
U-U(0)=-(∂lnQ/∂β)ᵥ (21.17), S=[U-U(0)]/T+kвlnQ (21.22)
p.s. Q可以從qN/N! 或 qN求得
(1) A=U-TS, and A(0)=U(0)
(21.22)T, TS=U-U(0)+kвTlnQ→U-TS=U(0)-kвTlnQ, ⸫A=U(0)-kвTlnQ→A-A(0)=-kвTlnQ (21.12)
(2)⸪ (∂A/∂V)ᴛ=-p, ⸫ p=(∂kвTlnQ/∂V)ᴛ=kвT(∂lnQ/∂V)ᴛ (21.13)
ex. use Q=qN/N! and qᵀ=V/Λ³ to derive ideal gas eq. pV=nRT
p=kвT(∂lnQ/∂V)ᴛ=kвT[∂ln(qN/N!)/∂V]ᴛ=kвTN(∂lnq/∂V)ᴛ-kвT(∂lnN!/∂V)ᴛ=nRT(∂lnq/∂V)ᴛ
=nRT(∂lnqᵀqᴿqVqᴱ/∂V)ᴛ=nRT(∂lnqᵀ/∂V)ᴛ=nRT(∂qᵀ/∂V)ᴛ/qᵀ=nRT(1/Λ³)/(V/Λ³)=nRT/V
(3)H=U+pV, and H(0)=U(0)
(21.17)+(21.13)V, H=U(0)-(∂lnQ/∂β)ᵥ+kвTV(∂lnQ/∂V)ᴛ
→H-H(0)=-(∂lnQ/∂β)ᵥ+kвTV(∂lnQ/∂V)ᴛ (21.24)
(4)G=H-TS=U+pV-TS=A+pV=A(0)-kвTlnQ+kвTV(∂lnQ/∂V)ᴛ, G(0)=A(0)
→G-G(0)=-kвTlnQ+kвTV(∂lnQ/∂V)ᴛ or G-G(0)=-kвTlnQ+nRT (21.25)
ex. in the case of non-interacting particles, Q=qN/N!
G-G(0)=-kвTlnQ+nRT=-kвT(Nlnq-lnN!)+nRT=-nRTlnq+kвT(NlnN-N)+nRT=-nRT(lnq-lnN)
→G-G(0)=-nRTln(q/N)=-nRTln(qₘ/Nᴀ) i.e. qₘ=q/n
附註:






