固態物理: 倒晶格 - 人生紀錄本

Contents ...

udn網路城邦

固態物理: 倒晶格

2021/02/14 16:19

迴響0

推薦0

引用0

Chap. 2 Reciprocal lattice

crystal structure: basis + lattice

bobe beam for studying crystal structure: 1. x rays 光子與electron作用, =1-10Å. 2. neutron nuclei. 3. electron

Bragg’s law

2dsin=n 加強性干涉

n(r) electron concentration charge density, r=r+T 滿足週期性關係

satisfied n(r+T )=n(r)=n( r) → n( r)≡periodic, T =u₁a₁+u₂a₂+u₃a₃

consider 1-D n(x+a)=n(x), T =u₁a₁, n(x) can be represented by a Fourier series

n(x)=n_₀+∑ₚ_>_₀[Cpcos(2πpx/a)+Spsin(2πpx/a)]

n(x+a)=n_₀+∑ₚ_>_₀[Cpcos(2πpx/a+2πp)+Spsin(2πpx/a+2πp)]=n(x)

n(x)=n_₀+∑ₚ_>_₀[Cp(eⁱ²^π^px^/^a+e^-ⁱ²^π^px^/^a)/2-iSp(eⁱ²^π^px^/^a-e^-ⁱ²^π^px^/^a)/2]

=n_₀₊_∑ₚ_>_₀[eⁱ²^π^px^/^a(Cp-iSp)/2+e^-ⁱ²^π^p^x/a(Cp+iSp)/2]

=∑pnp eⁱ²^π^px/a

Cp, Sp are real, n-p=np* n-p=½( Cp-iSp), np*=½( Cp+iSp)

n(x)=∑pnp eⁱ²^π^px/a → 2π/a is 1-D reciprocal lattice vector.

In 3-D, we have to define a vector G and satisfy n(r+T )=n(r)=n(r)

n(r)=∑_Gn_Geⁱ^G^•^r

倒空間平移向量: G=v₁b₁+v₂b₂+v₃b₃,

b₁=2π[(a₂a₃)/(a₁•a₂a₃)], b₂=2π[(a₃a₁)/(a₁•a₂a₃)], b₃=2π[(a₁a₂)/(a₁•a₂a₃)]

i.e. V= a₁•a₂a₃

b₁•a₁=2π , b₁•a₂=0, b₁•a₃=0. If a₁, a₂, a₃ are primitive axes, then b₁, b₂, b₃ are primitive axes.

bᵢ•a_j=2πδᵢ_j, δᵢ_j=1(i=j) or δᵢ_j=0(i≠j)

→ reciprocal lattice used in x ray diffraction

n(r+T )=∑_Gn_Geⁱ^G^•⁽^r⁺^T⁾=∑_Gn_Geⁱ^G^•^r∑_Gn_Geⁱ^G^•^T=n(r)eⁱ²^π(^v^₁^u^₁^+v^₂^u^₂+v₃^u^₃⁾=n(r)

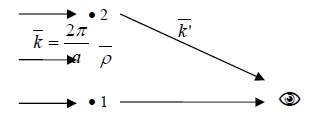
the amplitude of an incident plane wave at r is A=A₀eⁱ⁽^k^•^r^-^wt⁾

at site 1, amplitude is A=A₀e^-^iwt

at site 2, amplitude is A=A₀eⁱ⁽^k^•^ρ^-^wt⁾

x ray scattered from #1 electron, amplitude =2k•G=|G|²

Step 1. if G=hb₁+kb₂ +lb₃ then G is normal to the crystal plane (h,k,l)

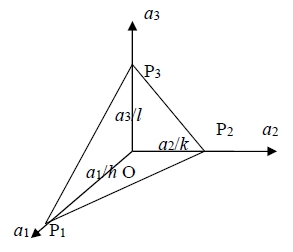
找平面的法線方向, n=P₁P₂P₁P₃=(a₂/k-a₁/h)(a₃/l-a₁/h)=1/kl(a₂a₃)-1/hl(a₁a₃)-1/hk(a₂a₁)

n=1/kl(a₂a₃)-1/hl(a₁a₃)-1/hk(a₂a₁)=(1/hkl)[h(a₂a₃)+k(a₃a₁)+l(a₁a₂)]

=((a₁•a₂a₃)/2πhkl){2π[h(a₁a₂)/(a₁•a₂a₃)]+2π[k(a₃a₁)/(a₁•a₂a₃)]+2π[l(a₂a₃)/(a₁•a₂a₃)]}

=((a₁•a₂a₃)/2πhkl)[hb₁+kb₂ +lb₃]=(V/2πhkl) G // G ⸪ n // G ⸫ G ┴ (hkl)

Step 2. 平面間距離 d₍_hkl₎=2π/|G|

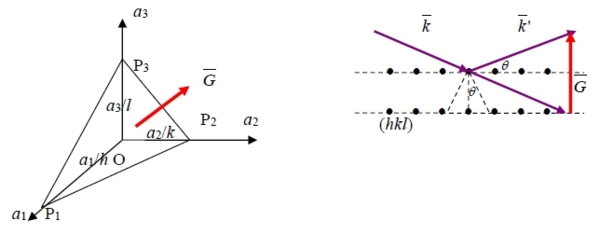
包含通過原點與(hkl)平行的面, OP₁•G=|OP₁||G|cosθ → d₍_hkl₎=|OP₁|cosθ=(OP₁•G)/|G|=

{(a₁/h)•[hb₁+kb₂ +lb₃]}/|G|=2π/|G|

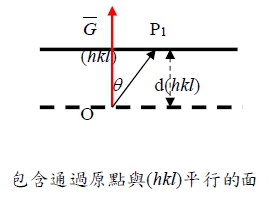
Step 3. 2k•G=|G|²

k+G=k → k-k=G i.e. |k|=|k|

k²=k•k=|k|²=(k+G)•(k+G)=|k|²+2k•G+|G|² → 2k•G+|G|²=0 → 2k•(-G)+|-G|²=0 → 2k•G=|G|²

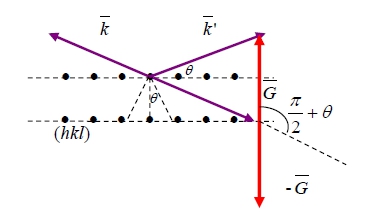
2|k||G|cos(90°+θ)+|G|²=0 → -2|k||G|sinθ+|G|²=0 → 2|k|sinθ=|G|=2πn/d₍_hkl₎

→ 2(2π/λ)sinθ=2πn/d₍_hkl₎⸫ 2d₍_hkl₎sinθ=nλ another statement of Bragg’s law

Laue equation: 找k的方向, k-k=Δk =G if G=v₁b₁+v₂b₂+v₃b₃

→ a₁•Δk =a₁•G=2πv₁, a₂•Δk =2πv₂, a₃•Δk =2πv₃

Edwald construction

Brillouin zones: is defined as a wigner-seitz primitive cell in the reciprocal lattice.

Diffraction condition: 2k•G=|G|²除以4, k•(G/2)=|G/2|²

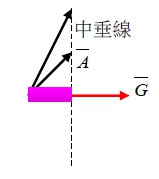
A•(G/2)=|A||G/2|cosθ=|A|cosθ|G/2|=|G/2|²

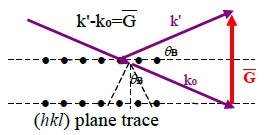
G₁⊥原子平面跡 (plane trace), 原子平面跡是k₀及k的分角線1/2|G|=|k₀|sinθ_ᴃ , |k₀|=1/λ, λ=2/|G|sin θ_ᴃ, 與λ=2d sin θ_ᴃ 比較, |G|=1/d ,且G //原子平面之法向量（有建設性干涉的原子平面⊥原子平面跡

{G}代表晶體可產生“建設性”干涉的平面組,其方向為平行平面之法向量且長度為對應的平面間距

實空間與倒空間(晶體結構與繞射花樣 (Band Gap)為何需要另一個空間?

•倒空間能使我們方便描述及處理晶體繞射的問題

•事實上,“倒”晶格空間和“實”晶格空間一樣的“真實”

•我們可以把晶體想成有兩個“晶格”一個“實”晶格,一個“倒”晶格實晶格是晶體本身,倒晶格則是繞射空間的點陣

1) 倒空間: 與實空間一樣真實

2) 倒空間的一點相對於實空間的一平面

3)倒空間的一點至原點的距離等於平面間距的倒數

Real space vs. Reciprocal space

實空間平移向量,r=n₁t₁+n₂t₂+n₃t₃, primitive cell是晶體中只含一個原子的unit cell, 以primitive unit cell為單位取實空間平移向量, e.g. BCC

t₁=a/2(-x+y+z), t₂=a/2(x-y+z), t₃=a/2(x+y-z)

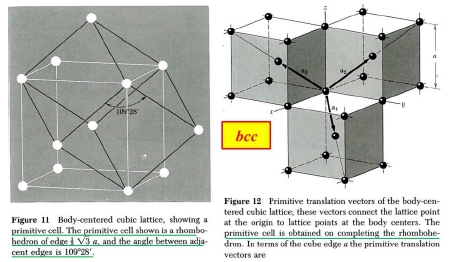
b₁=2π[(t₂t₃)/(t₁•t₂t₃)], b₂=2π[(t₃t₁)/(t₁•t₂t₃)], b₃=2π[(t₁t₂)/(t₁•t₂t₃)] i.e. V= t₁•t₂t₃

→ b₁=2π[(a²/4)(2y+2z)]/(a³/2)=2π/a(y+z)=2π/a(011), b₂=2π/a(101), b₃=2π/a(110)

reciprocal lattice to S.C. lattice

crystal lattice: a₁=ax, a₂=ay, a₃=az V=a₁∙a₂a₃=a³

reciprocal lattice: b₁=(2π/a)x, b₂=(2π/a)y, b₃=(2π/a)z V=b₁∙b₂b₃=(2π/a)³

remind**G=v₁b₁+v₂b₂+v₃b₃,

b₁=2π(a₂a₃/a₁∙a₂a₃), b₂=2π(a₃a₁/a₁∙a₂a₃), b₃=2π(a₁a₂/a₁∙a₂a₃)

b₁∙a₁=2π, b₁∙a₂=0, b₁∙a₃=0

第一不連續的cubic邊長=2/a

the boundary of the 1^st Brillouin zone: the planes normal to the six reciprocal lattice vectors: ±½b₁=±(π/a)x, ±½b₂=±(π/a)y, ±½b₃=±(π/a)z

reciprocal lattice to B.C.C. lattice

crystal lattice: a₁=a/2(-x+y+z), a₂=a/2(x-y+z), a₃=a/2(x+y-z) V=|a₁∙a₂a₃|

=(a/2)³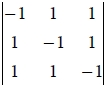 = a³/2

reciprocal lattice:

b₁=(2π/a)(y+z), b₂=(2π/a)(x+z), b₃=(2π/a)(x+y)

V=b₁∙b₂b₃=(2π/a)³ =2(2π/a)³ volume of 1^st BZ of B.C.C. lattice

→B.C.C. 的reciprocal lattice = F.C.C.的晶格

the boundary of the 1^st Brillouin zone: the planes normal to the twelve reciprocal lattice vectors: b₁=(π/a)(±y±z), b₂=(π/a)(±x±z), b₃=(π/a)(±x±y)

reciprocal lattice to F.C.C. lattice

crystal lattice: a₁=a/2(y+z), a₂=a/2(x+z), a₃=a/2(x+y)

V=|a₁∙a₂a₃|=(a/2)³ = a³/4

reciprocal lattice: b₁=(2π/a)(-x+y+z), b₂=(2π/a)(x-y+z), b₃=(2π/a)(x+y-z)

→F.C.C. 的reciprocal lattice = B.C.C.的晶格

第一不連續的 8 vectors: (π/a)(±x±y±z)

Fourier analysis of the basis

Consider one cell, the amplitude of x ray scatter from a crystal of N cells can be written as:

F_G=N∫_сеӏӏdVn(r)e^-ⁱ^∆^k^∙^r=N∫_сеӏӏdVn(r)e^-ⁱ^G^∙^r=N∙S_G

structure factor, S_G=∫_сеӏӏdVn(r)e^-ⁱ^G^∙^r, 分成atom, electron兩邊討論

S_G=∫_сеӏӏdVn(r)e^-ⁱ^G^∙^r=∫_сеӏӏdV∑_jn_j(r-r_j)e^-ⁱ^G^∙^r=∑_j∫_сеӏӏdVn_j(r-r_j)e^-ⁱ^G^∙^r,

let ρ=r-r_j →S_G=∑_j∫_сеӏӏdVn_j(_ρ)e^-ⁱ^G^∙^r在積分號r_j為常數

S_G=∑_j∫_сеӏӏdVn_j(_ρ)e^-ⁱ^G^∙(^ρ⁺^r^j⁾=∑_j∫_сеӏӏdVn_j(_ρ)e^-ⁱ^G^∙^ρe^-ⁱ^G^∙^r^j=∑_je^-ⁱ^G^∙^r^j∫_сеӏӏdVn_j(_ρ)e^-ⁱ^G^∙^ρ

=∑_je^-ⁱ^G^∙^r^j∙f_j

f_j: 考慮何種atom對電子的影響, we called it atom form factor.

首項級數和: 是考慮atom的位置, 亦即晶體結構的影響

考慮basis中的atom位置 r_j=x_ja₁+y_ja₂+z_ja₃ 0≤x_j, y_j, z_j≤1

G=v₁b₁+v₂b₂+v₃b₃, bᵢ∙a_j=2πδᵢ_j, δᵢ_j=0(i≠j) or δᵢ_j=1(i=j)

G ∙r_j=2π(v₁x_j+v₂y_j+v₃z_j) → S_G=∑_je^-i2^π⁽^v^₁^xj⁺^v^₂^yj⁺^v^₃^zj⁾∙f_j

Structure factor of the S.C. lattice

basis = one atom (0,0,0) → S_G=f_je^-i2^π⁽⁰⁾=f

any set of (v₁,v₂,v₃) can satisfy the constructive diffraction condition.

Structure factor of the B.C.C. lattice

conventional cell: positions of atoms→ (0,0,0), (½,½,½)

S_G=∑_je^-i2^π⁽^v^₁^xj⁺^v^₂^yj⁺^v^₃^zj⁾∙f_j=f∙e^-i2^π⁽⁰⁾+f∙e^-i^π⁽^v^₁^+v^₂^+v^₃⁾=f∙[1+e^-i^π⁽^v^₁^+v^₂^+v^₃⁾]

e^-ⁱ^θ=cosθ-isinθ, θ=nπ if v₁+v₂+v₃=2n, S_G=2f (constructive) or v₁+v₂+v₃=2n+1, S_G=0 (destructive)

Structure factor of the F.C.C. lattice

positions of atoms→ (0,0,0), (½,0,½), (½,½,0), (0,½,½)

S_G=f∙[1+e^-i^π⁽^v^₂^+v^₃⁾+e^-i^π⁽^v^₁^+v^₃⁾+e^-i^π⁽^v^₁^+v^₂⁾]

if (i)v₁+v₂+v₃=2n, S_G=4f (constructive) (ii)v₁+v₂+v₃=2n+1, S_G=4f (constructive) (iii)1odd, 2even → S_G=0 (destructive) (iv)2odd, 1even → S_G=0 (destructive)

ex. Structure factor of KCl

position of atom in a cell:

Cl^- : (0,0,0), (½,0,½), (½,½,0), (0,½,½)

K⁺ : (½,½,½), (0,0,½), (0,½,0), (½,0,0)

S_G=f(K⁺)[e^-i^π⁽^v^₁^+v^₂^+v^₃⁾+e^-i^π^v^₁+e^-i^π^v^₂+e^-i^π^v^₃]+f(Cl⁻)[1+e^-i^π⁽^v^₂^+v^₃⁾+e^-i^π⁽^v^₁^+v^₃⁾+e^-i^π⁽^v^₁^+v^₂⁾]

if (i)v₁+v₂+v₃=2n, S_G=4[f(K⁺)+f(Cl⁻)] (constructive) (ii)v₁+v₂+v₃=2n+1, S_G=4f[f(Cl⁻)-f(K⁺)]≈0 (⸪Cl⁻≈K⁺) (iii)1odd, 2even → S_G=0 (destructive) (iv)2odd, 1even → S_G=0 (destructive)