量子概念事件簿 - 人生紀錄本

Contents ...

udn網路城邦

量子概念事件簿

2023/05/02 15:00

迴響0

推薦0

引用0

古典牛頓力學無法解釋原子以下的粒子行為,1926出現量子力學

古典描述方法: (i)粒子能量 E=½mv²+V, i.e. p=mv, x(t) & v(t), or E=p²/2m+V 因為p=m(dx/dt),它是x(t)的微分方程,可以得出粒子的軌跡位置; if V=0, E=½mv² or (2E/m)^1/2=dx/dt, 得解x(t)=x(0)+(2E/m)^1/2t or x(t)=x(0)+p(0)t/m if E=constant.

(ii) ṗ=dp/dt=F or m(d²x/dt²)=F如果知道施力的函數F(t),一樣可得粒子的軌跡: ex. dp/dt=F₀ 0<t<τ (a), dp/dt=0 t≥τ (b) 得解p(t)=p(0)+ F₀t 0<t<τ and p(τ)=p(0)+ F₀τ t≥τ, 假設p(0)=0,粒子動能為p²/2m=F₀²τ²/2m,F與t可以取任何值,因此粒子能量也可以取任何值

另外角動量與扭力: J=Iω類似p=mv, J=T and 旋轉能T²τ²/2I; 簡諧振盪:粒子受恢復力F=-kx作用m(d²x/dt²)=-kx, 解為x(t)=Asinωt, ω=(k/m)^1/2, p=mẋ=mωAcosωt with freq.=ω/2π, 當x=A, 動量p最小;x=0時p最大, E=½mv²+V=p²/2m+½kx²=m²ω²A²cos²ωt/2m+kA²sin²ωt/2=kA²/2, i.e. F=-dV/dx=-kx, V= ½kx²

上述古典物理的例子都能預測準確的軌跡,而且控制施力就可得任何的能量,但是當處理非常小的質點或能量時,變得無法同時得知x與p描述粒子的軌跡,能量傳遞也不是連續的

古典物理的失敗

(a)黑體輻射:有2個特色,其一為輻射能量峰值隨溫度升高往短波長移動(Tλₘₐₓ=2.910⁻³mK),另外是能量密度與溫度的關係(Stefans law, U=aT⁴ or M=σT⁴, σ=5.6710⁻⁸Wm⁻²K⁻⁴).

R-J古典理論: 黑體內電磁場看成簡諧振盪子的組合,代表每一種頻率的光,根據等分原理,每個振子的平均能量是k_BT, 因此介於λ到λ+dλ的能量密度dU(λ)=k_BTdN(λ), N(λ)是單位體積的振子數,R-J law: dU(λ)=ρ(λ)dλ, ρ(λ)=8πk_BT/λ⁴

pf: 假設黑體邊長為a, 形成駐波的波長 a=n∙(λ/2), λ=2a/n or n=2a/λ, n=1,2,3...每一允許的波長,對應著不同的n,代表電磁波的能態 (state),因此我們可以在此黑體空間中對n 作積分,

n_x=2a/λ_x, n_y=2a/λ_y, n_z=2a/λ_z, → n(λ)=(n_x²+n_y²+n_z²)^1/2=2a/λ 若將n(λ)設為空間中的向量,並令為r,則在r→r+dr的球殼體積為dV(r)=4πr²dr 然而因為n_x ,n_y ,n_z皆為正整數,所以只考慮該體積的1/8為符合實際討論的條件,所以dV(r)=⅛(4πr²dr)=πr²dr/2, r= 2a/λ

⸪ c=λυ, r(υ)=2aυ/c and dr=2adυ/c → dV(r)=½π(2aυ/c)²2adυ/c=π(2a/c)³υ²dυ/2

考慮電磁波有兩個偏極方向所以上式應再乘上2, n(υ)=π(2a/c)³υ²dυ

除以體積a³ ,則代表空腔中的density of state, N(υ)=8π(2υ²/c³)dυ, 依據equipartition 定律,每個state 的平均能量為k_BT,因為在空腔中來回振盪多次,變成平均能量,所以 energy density in υ→υ+dυ is: dU(λ)=ρ(υ)dυ=N(υ)*k_BT=8π(2υ²/c³)k_BTdυ=(8πk_BT/λ²c)(-cdλ/λ²)=-8πk_BTdλ/λ⁴=-ρ(λ)dλ

⸫ ρ(λ)=8πk_BT/λ⁴ 但是此公式導致紫外線大災難

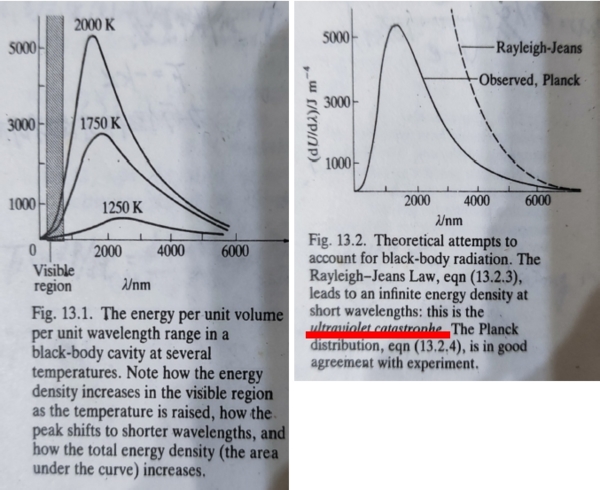
普朗克分佈: dU(λ)=ρ(λ)dλ, ρ(λ)=8πℎc/λ⁵[e^-^hc^/^k^ᴮ^Tλ/(1-e^-^hc^/^k^ᴮ^Tλ)]

Max Planck從熱力觀點提出能量量子化(εₙ=nhυ, n=0,1,2,3...)的假設去解釋實驗觀察,黑體內腔壁的粒子做熱振動,激發空腔內的電磁振子(光子)的能量,只可以是量子化

定性的看ρ(λ): 當波長變小,頻率變大, 若hυ/k_ᴮT→∞則e^-^hυ^/^k^ᴮ^T→0, ρ(λ)→0;當波長變大,頻率變小, 若hc/k_ᴮTλ<<1則e^-^hc^/^k^ᴮ^Tλ≈1-hc/k_ᴮTλ, e^-^hc^/^k^ᴮ^Tλ/(1-e^-^hc^/^k^ᴮ^Tλ)=(1-hc/k_ᴮTλ)/hc/k_ᴮTλ=k_ᴮTλ/hc-1≈ k_ᴮTλ/hc

→ ρ(λ)=(8πℎc/λ⁵)(k_ᴮTλ/hc)=8πk_ᴮT/λ⁴等於R-J law公式

同時普朗克分佈也可以解釋剛開始提到的特色:

(i)Wiens law Tλₘₐₓ=2.910⁻³mK: 求λₘₐₓ, dρ(λ)/dλ=0 → (8πℎc)dλ⁻⁵(e^hc^/^k^ᴮ^Tλ-1)⁻¹/dλ=0

dλ⁻⁵(e^hc^/^k^ᴮ^Tλ-1)⁻¹/dλ=-5λ⁻⁶(e^hc^/^k^ᴮ^Tλ-1)⁻¹-λ⁻⁵(e^hc^/^k^ᴮ^Tλ-1)⁻²e^hc^/^k^ᴮ^Tλ(-hc/k_ᴮTλ²)=0, let x=hc/k_ᴮTλ,

-5λ⁻⁶(e^x-1)⁻¹-λ⁻⁵(e^x-1)⁻²e^x(-x/λ)=0 → λ⁻⁶(e^x-1)⁻²[-5(e^x-1)+xe^x]=0 → (5-x)e^x=5, x=0 or 4.9651

⸫ hc/k_ᴮTλ=4.9651, λₘₐₓ=hc/4.97k_ᴮT=b/T, b=hc/4.97k_ᴮ=2.8910⁻³mK

(ii) Stefans law, U=aT⁴ or M=σT⁴, σ=5.6710⁻⁸Wm⁻²K⁻⁴

dU(λ)=ρ(λ)dλ, U=∫₀^∞ρ(λ)dλ=∫₀^∞8πℎc/λ⁵[e^-^hc^/^k^ᴮ^Tλ/(1-e^-^hc^/^k^ᴮ^Tλ)]dλ, let x=hc/k_ᴮTλ, dx=(-hc/k_ᴮTλ²) dλ

→ U=∫₀^∞8πℎc/λ⁵[e^-^hc^/^k^ᴮ^Tλ/(1-e^-^hc^/^k^ᴮ^Tλ)]dλ=∫_∞^₀(8πk_ᴮ⁴T⁴/ℎ³c³)(hc/k_ᴮTλ)³[e⁻^x/(1-e⁻^x)](-hc/k_ᴮTλ²)dλ

=(8πk_ᴮ⁴/ℎ³c³)T⁴∫₀^∞[x³e⁻^x/(1-e⁻^x)]dx=(8π⁵k_ᴮ⁴/15ℎ³c³)T⁴, a=8π⁵k_ᴮ⁴/15ℎ³c³

i.e. e⁻^x/(1-e⁻^x)=e⁻^x(1+e⁻^x+e⁻²^x+e⁻³^x+...)=e⁻^x+e⁻²^x+e⁻³^x+...=∑ₙ₌₁^∞e^-^nx, ζ(s)Γ(s)=∫₀^∞[x^s⁻¹e⁻^x/(1-e⁻^x)]dx

s=4, ζ(4)Γ(4)=(π⁴/90)(4-1)!=π⁴/15

R-J古典理論與普朗克分佈的差異:

兩者的能態密度N(λ)都相同,主要在能量的形式不同,古典採能量均分且連續的概念,所以平均能量ε=k_ᴮT; 普朗克則認為能量分佈不連續且與頻率有關,εᵢ=ihυ, i=0,1,2,3...

平均能量ε的計算

R-J古典理論: 能量採Boltzmann機率分佈(P(ε)=Ae^-^ε^/^k^ᴮ^T),因連續使用積分表示

ε=∫₀^∞εAe^-^ε^/^k^ᴮ^Tdε/∫₀^∞Ae^-^ε^/^k^ᴮ^Tdε (13.1)

分子部分用部分積分: 設u=ε, dv=e^-^ε^/^k^ᴮ^Tdε → v=-k_ᴮTe^-^ε^/^k^ᴮ^T; ∫udv=uv-∫vdu 代入u,v

∫₀^∞εe^-^ε^/^k^ᴮ^Tdε=-k_ᴮTεe^-^ε^/^k^ᴮ^T|₀^∞-∫₀^∞-k_ᴮTe^-^ε^/^k^ᴮ^Tdε=k_ᴮT∫₀^∞e^-^ε^/^k^ᴮ^Tdε 代入(13.1)

ε= k_ᴮT∫₀^∞e^-^ε^/^k^ᴮ^Tdε/∫₀^∞e^-^ε^/^k^ᴮ^Tdε=k_ᴮT

普朗克分佈: 能量同樣採Boltzmann機率分佈(P(εᵢ)=Ae^-^ε^ᵢ^/^k^ᴮ^T),因不連續使用級數加總表示

ε=(ℎc/λ)[e^-^hc^/^k^ᴮ^Tλ/(1-e^-^hc^/^k^ᴮ^Tλ)] (13.2)

ε=E/N=∑ᵢnᵢεᵢ/∑ᵢnᵢ=(N∑ᵢεᵢe^-^εᵢ/k^ᴮ^T/∑_ie^-^εᵢ/k^ᴮ^T)/∑ᵢnᵢ=∑ᵢεᵢe^-^εᵢ/k^ᴮ^T/∑_ie^-^εᵢ/k^ᴮ^T,

因為Boltzman分佈, 所以nᵢ=Ne^-^εᵢ/k^ᴮ^T/∑_je^-^εᵢ/k^ᴮ^T

let ∑_ie^-^εᵢ/k^ᴮ^T=q, β=1/k_ᴮT → ε=∑_iεᵢe^-^βεᵢ/∑_ie^-^βεᵢ=(-d[∑_ie^-^βεᵢ]/dβ)/∑_ie^-^βεᵢ=-d[ln∑_ie^-^βεᵢ]/dβ (13.3)

⸪ εᵢ=ihυ, i=0,1,2,3... ⸫ q=∑_ie^-^εᵢ/k^ᴮ^T=1+e^-^βε+e^-2^βε+e^-3^βε+...=1+e^-^βε+(e^-^βε)²+(e^-^βε)³+...=1/(1-e^-^βε) 代入(13.3)

ε=-d[ln∑_ie^-^βεᵢ]/dβ=-d[ln(1-e^-^βε)⁻¹]/dβ=εe^-^βε/(1-e^-^βε)=hυe^-^hυ^/k^ᴮ^T/(1-e^-^hυ^/k^ᴮ^T)=(ℎc/λ)[e^-^hc^/^k^ᴮ^Tλ/(1-e^-^hc^/^k^ᴮ^Tλ)]

(b)晶體的比熱: 黑體輻射是解釋能量如何被電磁場吸收;比熱則是藉粒子振動吸收能量的反應.假設一塊有N個原子的晶體,每個原子都可以在三維上自由振動,振動的總能Eᵥ=3Nk_ᴃT=3nRT, R=N_ᴀk_ᴃ, 莫耳比熱Cᵥ_,ₘ=(∂Uₘ/∂T)ᵥ=3R, 即是古典的Dulong-Petits law.

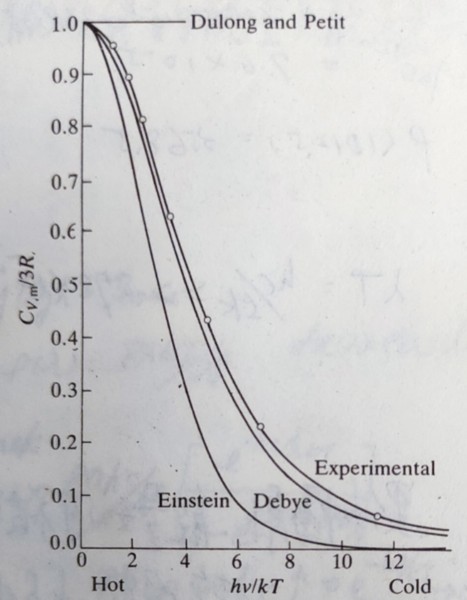
Einstein發現古典的比熱在低溫時,有明顯的差距,接近0 K比熱趨近於零,所以他採用普朗克假設:原子振動所吸收的能量都是相同的頻率υ,以hυ的能量子存在,晶體得到的振動能Eᵥ,

Eᵥ=3Nhυ[e^-^hυ^/k^ᴮ^T/(1-e^-^hυ^/k^ᴮ^T)]=3Nhυ/(e^hυ^/k^ᴮ^T-1) (13.4)

很像普朗克分佈導出的結果,振動比熱Cᵥ為:

Cᵥ=d[3Nℎυ/(e^hυ^/k^ᴮ^T-1)]/dT=3Nk_ᴃ(ℎυ/k_ᴃT)²[e^hυ^/k^ᴮ^T/(e^hυ^/k^ᴮ^T-1)²]=3R(ℎυ/k_ᴃT)²[e^hυ^/k^ᴮ^T/(e^hυ^/k^ᴮ^T-1)²] if N=N_ᴀ

令θ_ᴇ=ℎυ/k_ᴃ, Cᵥ=3R(θ_ᴇ/T)²[e^θ^ᴇ/^T/(e^θ^ᴇ/^T-1)²]

(i)高溫時 hυ/k_ᴃT<<1, font="">使得e^ℎ^ν^/kT≈1+hυ/k_ᴃT, Cᵥ=3R(hυ/k_ᴃT)²(1+ hυ/k_ᴃT)/(hυ/k_ᴃT)² ≈3R,

(ii)極低溫時hυ/k_ᴃT >>1, Cᵥ=3R(hυ/k_ᴃT)²e^-^h^υ^/^kᴃT→0比實驗值更快趨近於零

如何得到振動能Eᵥ?

晶格振動能, U=(i+½)ℎυ, i=1, 2, … 在0 K晶格振動能為½ℎυ, 加熱至T K,增加n個能量子ε =hυ ,使它們分布至N個原子的三維晶體中(3N個振子因為每個原子有3個自由度)讓亂度增加,即熵增加→ S=k_ᴃln[(n+3N)!/n!3N!]

利用自由能A=U-TS 在T K時吸收nhυ達熱平衡: dA/dn=dU/dn-T(dS/dn)=0

U=U₀+nhυ, U₀是0 K時的能量,所以 dU/dn=hυ

dS/dn=d{k_ᴃln[(n+3N)!/n!3N!]}/dn= k_ᴃln[(n+3N)/n] ⸫ hυ=k_ᴃTln[(n+3N)/n] → n=3N/(e^hυ^/k^ᴮ^T-1)

Eᵥ=nhυ=3Nhυ/(e^hυ^/k^ᴮ^T-1)

Debye將振動頻率的分佈考慮放入Cᵥ改寫為: Cᵥ=d[∑₁^3Nℎυᵢ/(e^hυᵢ^/k^ᴮ^T-1)]/dT

先求能量子的普朗克分佈: n=∑ₙnPₙ=(∑ₙne^-^β^εₙ)/(∑ₙe^-^β^εₙ), εₙ=nhυ, n=0,1,2,3... and β=1/k_ᴃT

n=(∑ₙne^-^β^εₙ)/(∑ₙe^-^β^εₙ)=(-1/hυ)[∂(ln∑ₙe^-^β^εₙ)/∂β]=(-1/hυ)[∂ln(1-e^-^β^ε)⁻¹/∂β]=(1/hυ)[εe^-^β^ε/(1-e^-^β^ε)]=e^-^β^ε/(1-e^-^β^ε)=1/(e^β^ε-1)=1/(e^hυ^/^k^ᴃ^T-1), i.e. ∑ₙe^-^β^εₙ=1+e^-^β^ε+e^-²^β^ε+e^-³^β^ε+...=1/(1-e^-^β^ε)

總能U=3∫₀^υnεD(υ)dυ 說明: 3代表聲子(原子)有三種極化,nε表示能量子的分佈,D(υ)dυ則是能態的數目,導出即可得總能

假設晶體為邊長L(V=L³)的立方體,振動形成駐波符合L=nλ=nc/υ, c=λυ, ⸫ υ=nc/L

每一個能態佔有體積=(c/L)³, 因為∆υ=υₙ-υₙ₋₁=c/L, 所以能態總數n(υ)=(4πυ³/3)/(c/L)³=4πυ³V/3c³

dn(υ)=D(υ)dυ=(4πυ²V/3c³)dυ

→ U=3∫₀^υnεD(υ)dυ=3∫₀^υ[1/(e^hυ^/^k^ᴃ^T-1)]hυ(4πυ²V/3c³)dυ=(12πVh/c³)∫₀^υ[υ³/(e^hυ^/^k^ᴃ^T-1)]dυ

let x=hυ/k_ᴃT=θ/T,→ U=(12πVh/c³)∫₀^θ/T(k_ᴃT/h)³[x³/(e^x-1)](k_ᴃT/h)dx=(12πVk_ᴃ⁴T⁴/c³h³)∫₀^θ/T[x³/(e^x-1)]dx

when υ=υ_ᴅ, x_ᴅ=hυ_ᴅ/k_ᴃT=θ_ᴅ/T i.e. θ_ᴅ: Debye溫度; n(υ_ᴅ)=4πυ_ᴅ³V/3c³=N, υ_ᴅ³=3c³N/4πV

(12πVk_ᴃ⁴T⁴/c³h³)=9Nk_ᴃT(4πV/3c³N)(k_ᴃT/h)³=9nRT(k_ᴃT/hυ_ᴅ)³=9nRT(T/θ_ᴅ)³

⸫ U=9nRT(T/θ_ᴅ)³∫₀^θ^ᴅ^/T[x³/(e^x-1)]dx

(1)at high T, hυ_ᴅ/k_ᴃT<<1, font="" face="Times New Roman, serif">e^x=1+x+x²/2!+x³/3!+...

∫₀^θ^ᴅ^/T[x³/(e^x-1)]dx=∫₀^θ^ᴅ^/T[x³/(1+x+x²/2!+x³/3!+...-1)]dx≈∫₀^θ^ᴅ^/Tx²dx=(θ_ᴅ/T)³/3, →U=3nRT, Cᵥ=3nR

(2)at very low T, hυ_ᴅ/k_ᴃT→∞, 1/(e^x-1)=e⁻^x+e⁻²^x+e⁻³^x+...=∑ₙ e⁻ⁿ^x

∫₀^∞[x³/(e^x-1)]dx=ζ(4)Γ(4)=3!(π⁴/90)=π⁴/15, →U= 3π⁴nRT(T/θ_ᴅ)³/5, Cᵥ=12π⁴nR(T/θ_ᴅ)³/5T ³

(c)光電效應: Einstein解釋紫外光照射金屬,測得電子從金屬射出,電子的動能遵守½mv²=hυ-Φ, hυ代表入射光子的能量, Φ則是金屬的功函數(使價電子游離的能量),此實驗把入射的光波看成粒子,想像成與電子碰撞,傳遞能量,造成電子游離射出.而且得到幾個特色: a.不管光的強度大小,光頻若小於金屬的閾值Φ,無法激發電子 b.激發電子的動能與光頻成正比 c.儘管光強度多低,只要光頻大於閾值Φ,電子也立即被激發

(d)Compton效應: 光與靜止的自由電子碰撞的散射實驗,發現散射後的光波長改變與散射角有關,與原波長無關: Δλ=λ_f-λᵢ=(h/mₑc)(1-cosθ), h/mₑc=2.43 pm:電子的Compton波長

上式可從能量與動量守恆得到,能量守恆須借用相對論能量公式((mc)²=p²c²+m₀²c⁴, m=m₀/[1-(v/c)²]^½), 在此不推導過程,舉一直觀的例子: 電子經過非彈性碰撞得到動能,假設速度為0.9c, K=mc²-mₑc²=(m-mₑ)c²≈ m‪ₑc², K=pc=m‪ₑc²→h/Δλ=m‪ₑc, Δλ=h/mₑc亦即電子所得動能是由光子碰撞前後的波長改變量所致!