Chap. 4 Phonon I crystal vibration

只考慮cubic system

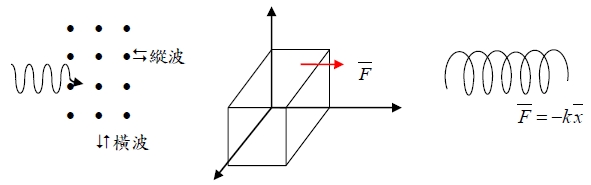
vibration of crystal with monatomic basis

聲波:介質粒子的振動 F=ma

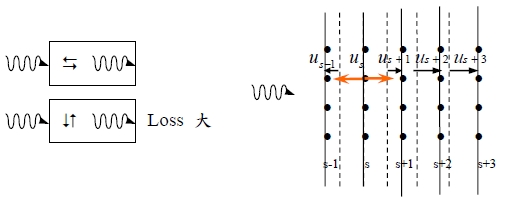
F₂=C₁(uₛ₊₁-uₛ)-C₋₁(uₛ-uₛ₋₁)=C₁(uₛ₊₁-uₛ)+C₋₁(uₛ₋₁-uₛ), Fₛ=∑ₚCₚ(uₛ₊ₚ-uₛ)=ma

m(d²u/dt²)=∑ₚCₚ(uₛ₊ₚ-uₛ) equation of motion

u_s=u(t) 猜解去try!!微分二次=本身→ e^x

try the traveling wave function: u_s= u₀e^i(kx-ωt)

x=sa, sZ代入u_s, → u_s=u₀e^i(ksa-ωt)

-mω²u_s=∑ₚCₚ[u₀e^i(ksa-ωt)(e^ikpa-1)] → -mω²=∑ₚCₚ(e^ikpa-1) i.e. k=2/ (wavevector)

consider C_n=C_-n, p>0

-mω²=∑ₚ_>₀Cₚ(e^ikpa-1)=∑ₚ_>₀[Cₚ(e^ikpa-1)+Cₚ(e^-ikpa-1)]=∑ₚCₚ(2coskpa-2)=-∑ₚ_>₀Cₚ2(1-coskpa) → ω²=∑ₚ_>₀2Cₚ/m(1-coskpa)

if only the interactions of the nearest neighboring are taken into account, p=1

ω²=2C₁/m(1-coska)=4C₁/m(sin²ka/2) ⸫ ω=(4C₁/m)^1/2|sinka/2|

independent to -π/a≤k≤ π/a, k=k±2nπ/a

u_s=u₀e^i(ksa-ωt) → u_s(k)=u_s(k), k=2π/λ, 0kπ/a 2π/λπ/aλ2a

=(k), v=/k group velocity v_g=d/dk=v_g(k)=a(C₁/m)^1/2coska/2, v_g(±π/a)=0表示能量沒有傳遞以standing wave形式

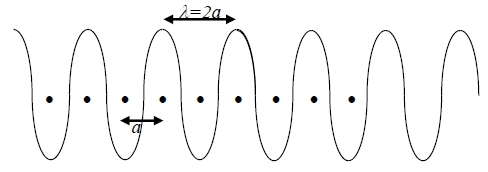
if k=±π/a, u_s=u₀e^i(ksa-ωt)=u₀e^i(sπ-ωt)=u₀(e^iπ )^se^-iωt=u₀(-1)^se^-iωt 只在原地振動

difference between an elastic continuum and lattice

if a→0, ka→0cos(kpa)=1-½(kpa)²+…

ω²=(2/m)∑ₚ_>₀Cₚ(1-coskpa)≈(2/m)∑ₚ_>₀(Cₚ/2)(kpa)²=(k²a²/m)∑ₚ_>₀Cₚp²=Ak²

→ ω=Ak ⸫ v_g=A

Lattice with two atoms per primitive cell

Fᴍ₁=M₁(d²u_s/dt²)=c(vₛ-u_s)+c(vₛ₋₁-u_s)=c(vₛ+vₛ₋₁-2u_s)...(1)

Fᴍ₂=M₂(d²v_s/dt²)=c(u_s₊₁-vₛ)+c(u_s-vₛ)=c(u_s₊₁+u_s-2vₛ)...(2)

u_s=ue^i(ksa-ωt), v_s=ve^i(ksa-ωt)

(1) -M₁ω²uₛ=c(vₛ+vₛe^-ika-2u_s) → -M₁ω²uₛ=cvₛ(1+e^-ika)-2cuₛ → (2c-M₁ω²)uₛ-c(1+e^-ika)vₛ=0

(2) -M₂ω²vₛ=c(uₛ+uₛe^ika-2v_s) → -M₂ω²vₛ=cuₛ(1+e^ika)-2cvₛ → (2c-M₂ω²)vₛ-c(1+e^ika)uₛ=0

for non-trivial solution of u and v

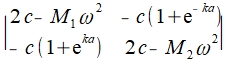=0 → M₁M₂ω⁴-2c(M₁+M₂)ω²+2c²(1-coska)=0

ω²=c(M₁+M₂)/M₁M₂{1±[1-2M₁M₂(1-coska)/(M₁+M₂)²]^1/2}

physical range of  =?  is real

|coska|≤1, coska=M₁M₂ω⁴/2c²-(M₁+M₂)ω²/c+1

 

(a) coska1

M₁M₂ω⁴/2c²-(M₁+M₂)ω²/c+11 → ω²[ω²-2c(M₁+M₂)/M₁M₂]0

⸫ ω[2c(1/M₁+1/M₂)]^1/2 when k=0, ω_max=[2c(1/M₁+1/M₂)]^1/2

 

(b) coska-1

M₁M₂ω⁴/2c²-(M₁+M₂)ω²/c+1≥-1 → ω⁴-2c(M₁+M₂)ω²/M₁M₂+4c²/M₁M₂≥0

→ (ω²-2c/M₁)(ω²-2c/M₂)≥0

if M₁>M₂, 2c/M₁<2c/M₂  ²>2c/M₂ or ²>2c/M₁ (when ka=π, k=π/a)

In the limiting case:

1. ka<<1

coska1-½k²a²

ω²=c(M₁+M₂)/M₁M₂{1±[1-2M₁M₂(1-coska)/(M₁+M₂)²]^1/2}

≈c(M₁+M₂)/M₁M₂{1±[1-2M₁M₂k²a²/(M₁+M₂)²]^1/2}

(取+) ω²=2c(1/M₁+1/M₂), (取-) ω²=ck²a²/2(M₁+M₂)

1. k=±π/a

ω²=c(M₁+M₂)/M₁M₂{1±[1-2M₁M₂(1-coska)/(M₁+M₂)²]^1/2}

=c(M₁+M₂)/M₁M₂[1±(M₁-M₂)/(M₁+M₂)]

ω²=2c/M₁ or ω²=2c/M₂

u_s=ue^i(ksa-ωt), v_s=ve^i(ksa-ωt)

(2c-M₁ω²)uₛ-c(1+e^-ika)vₛ=0, (2c-M₂ω²)vₛ-c(1+e^ika)uₛ=0

Am_M₁/Am_M₂=|u/v|=|c(1+e^-ika)/(2c-M₁ω²)|=|(2c-M₂ω²)/c(1+e^ika)|

|1+e^ika|=|1+coska+isinka|=[(1+coska)²+sin²ka]^1/2=(2+2coska)^1/2

=[4cos²(ka/2)]^1/2=2cos(ka/2)

⸫ |u/v|=2ccos(ka/2)/(2c-M₁ω²)=(2c-M₂ω²)/2ccos(ka/2)

For ka<<1

1. ω²=2c(1/M₁+1/M₂)

u/v=2ccos(ka/2)/(2c-M₁ω²)=2c(1+½(ka/2)²+...)/[2c-2c(1/M₁+1/M₂)]≈-M₂/M₁振幅反向,

i.e. cos(ka/2)=1+½(ka/2)²+...

1. ω²=ck²a²/2(M₁+M₂)→0, u/v≈1 振幅同向

case 1 consider ionic compound 造成反向

case 2 利用聲波產生”切應變” 造成同向

2 atoms per primitive cell or p atoms per primitive cell, if N cell, each atom has 3 degree of freedom→F_t=3Pn, each branch has N

 

ℏk=ℏk+ℏG elastic collision, p=ℏk, G :reciprocal vector

if inelastic, 晶體振盪→K:phonon ℏk=ℏk+ℏG±ℏK

 

 

 

 

 

 

 

註記: □=ℏ