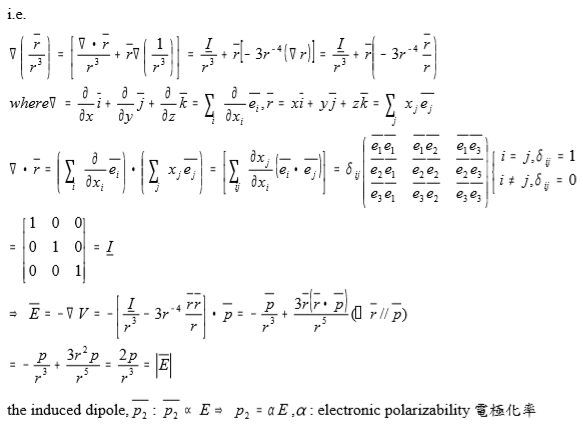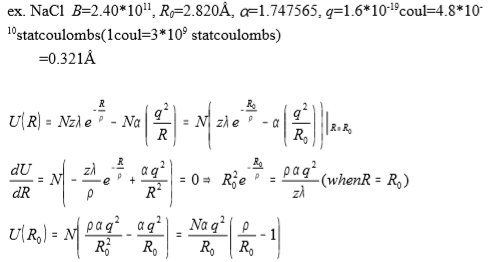Chap. 3 Crystal binding

Principle types of crystalline binding

1. crystal of inert gas(VIII A): van der Wals force; dipole-to-dipole interaction

2. ionic crystal: NaCl electrostatic force between ions(IA & VIIA)

3. covalent crystal: C, Si(IVA) quantum effect –spin repulsive or attractive by exchange force.

4. metallic crystal: Na, K(IA, B) charge attraction between positive and negative charges.

Crystal of inert gas

不考慮thermal vibration if –q分布中心在中心,則場效應=0

He	Ne	Ar	Kr	Xe
hcp	( fcc )
1s²	1s² 2s² 2p⁶	(Ne) 3s² 3p⁶	(Ar) 3d¹⁰ 4s² 4p⁶	(Kr) 4d¹⁰ 5s² 5p⁶

if thermal vibration at 0K, zero-point energy = ½ℏω=½cu²=½mw²u²

u²^1/2平均距離, u:位移, c:彈性係數 k

binding force in the inert gas crystal at instant t :

the interaction energy between two diploes, p₁, p₂, separated by R is given by

U(R)=(p₁∙p₂)/R³-3(p₁∙R)(p₂∙R)/R⁵ → U(R)=(p₁∙p₂)/R³-3(p₁∙p₂)/R³=-2(p₁∙p₂)/R³

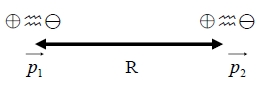
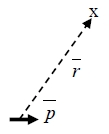
V=p∙R/R³, E=-V=-(p∙R/R³)=-p∙(R/R³)-(R/R³)∙ p

p=0, 與電荷密度有關∵r距離太遠

i.e.

(R/R³)=[∙R/R³+R(1/R³]=I/R³+R[-3R⁻⁴(R)]=I/R³+R[-3R⁻⁴(R/R)]

where =(∂∕∂x)i+(∂∕∂y)j+(∂∕∂z)k=∑ᵢ (∂∕∂xᵢ)eᵢ, r=xi+yj+zk=∑_j x_j e_j ,

∙r=[∑ᵢ (∂∕∂xᵢ)eᵢ]∙[∑_j x_j e_j]=[∑ᵢ_j (∂x_j ∕∂xᵢ)(eᵢ∙e_j )]=δᵢ_j=

=I, i.e. δᵢ_j=1 if i=j or δᵢ_j=0 if i≠j

E=-V=-[I/R³-3R⁻⁴(R∙R/R)]∙p=-p/r³+3R(R∙p/R⁵)=-p/R³+3R²p/R⁵=2p/R³=|E| ⸪ R// p

the induced dipole, p₂ : p₂ E→p₂=αE, : electronic polarizability電極化率

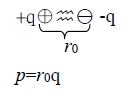
⸫ p₂=α(2p/R³)=2αqr₀/R³ and U(R)=-2(p₁∙p₂)/R³=(-2/R³)∙r₀q∙(2αqr₀/R³)

=-4α(r₀q)²/R⁶=-A/R⁶ → F=-U=-dU/dR  1/R⁷

Quantum derivation of van der Waals force

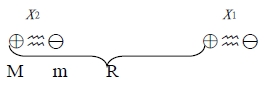
total energy, H=(p₁²/2m+½cx₁²)+(p₂²/2m+½cx₂²)+H₁, H₁: 靜電位能

ex. H原子, Eₙ=(n+½)ℏω

H₁=e²/R-e²/(r+x₁)-e²/(R-x₂)+e²/(R-x₂+x₁)

⸪ x₁, x₂<<R → (1+R/r)⁻¹=1-x/R+(x/R)²-(x/R)³+... Taylor series

H₁=e²/R-e²/R[1-x₁/R+(x₁/R)²-(x₁/R)³+...]-e²/R[1-x₂/R+(x₂/R)²-(x₂/R)³+...]+e²/r[1-(x₂-x₁)/R+(x₂-x₁)²/R²-(x₂-x₁)³/R³+...] → H₁≈-2e²x₁x₂/R³

H=(p₁²/2m+½cx₁²)+(p₂²/2m+½cx₂²)-2e²x₁x₂/R³

let xₛ=1/√2(x₂+x₁), xₐ=1/√2(x₁-x₂) → x₁=1/√2(xₛ+xₐ), x₂=1/√2(xₛ-xₐ)

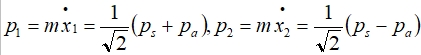
H=(p₁²/2m+½cx₁²)+(p₂²/2m+½cx₂²)-2ex₁x₂/R³

={[1/√2(pₛ+pₐ)²/2m]+½c[1/√2(xₛ+xₐ)]²}+{[1/√2(pₛ-pₐ)²/2m]+½c[1/√2(xₛ-xₐ)]²}-2e²[1/√2(xₛ+xₐ)][1/√2(xₛ-xₐ)]/R³

=[½(pₛ²+2pₛpₐ+pₐ²+pₛ²-2pₛpₐ+pₐ²)]/2m+c/2[½(xₛ²+2xₛxₐ+xₐ²)+½(xₛ²-2xₛxₐ+xₐ²)]-e²(xₛ²-xₐ²)/R³=pₛ²/2m+pₐ²/2m+½cxₛ²+½cxₐ²-e²(xₛ²-xₐ²)/R³

=[pₛ²/2m+½(c-2e²/R³)xₛ²]+[pₐ²/2m+½(c+2e²/R³)xₐ²]

∵為Simple Harmonic motion Eₙ=(n+½)ℏω₀

if H=H₀+H₁ H=E  (H₀+H₁)=E  H₀+H₁=E

*The zero point energy(n=0) of the system

½ ħ(ω_s+ω_a)—with dipole-to-dipole interaction, H₀+H₁(E_p.p.+ E_0-0)

½ ħ(ω₀+ω₀)—without D-D interaction(E_0-0)

∆U=½ ħ(ω_s+ω_a)-½ ħ(ω₀+ω₀)

ω₀=(c/m)^1/2, ω_s=[(c-2e²/R³)/m]^1/2=(c/m)^1/2[1-½(2e²/cR³)-⅛(2e²/cR³)²+...]

ω_a=[(c+2e²/R³)/m]^1/2=(c/m)^1/2[1+½(2e²/cR³)-⅛(2e²/cR³)²+...]

→ ∆U=½ ħ(ω_s+ω_a)-½ ħ(ω₀+ω₀)≈ ½ ħ[ω₀+ω₀-¼ω₀ (2e²/cR³)²]-½ ħ(ω₀+ω₀)

=-ℏω₀/8(2e²/cR³)²

Repulsive interaction—due to the overlapping of electron orbit[Pauli exclusion principle]

Empirical form B/R¹²

the total potential energy of two inert gas atoms at separation R is

U(R)=B/R¹²-A/R⁶=4ε[(σ/R)¹²-(σ/R)⁶]

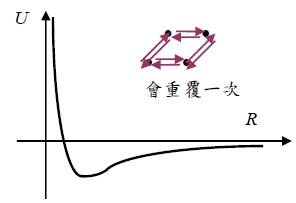
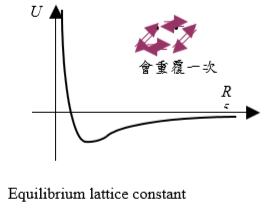
Equilibrium lattice constant

Uₜₒₜₐₗ=½∑ᵢ ∑_j U_ij=½∑_j (∑ᵢU_ij)=(N/2)∑_jU_ij

now U_ij=4ε[(σ/R_ij)¹²-(σ/R_ij)⁶ ] let R_ij=P_ij R → U_ij=4ε[(1/P_ij)¹²(σ/R)¹²-(1/P_ij)⁶(σ/R)⁶]

Uₜₒₜₐₗ=½N4ε[∑_j(1/P_ij)¹²(σ/R_ij)¹²-∑_j(1/P_ij)⁶(σ/R_ij)⁶]

For inert gas crystal, in addition to He.

1. nearest neighbors: 12, P_ij=1 and R=a/√2

2. second nearest neighbors: 6, P_ij=√2 and R’=√2R=a

3. third nearest neighbors: 12, P_ij=2 and R”=2R=√2a….

∑_j(1/P_ij)¹²=12∙1⁻¹²+6∙√2⁻¹²+12∙2⁻¹²+...=12.1388

∑_j(1/P_ij)⁶=12∙1⁻⁶+6∙√2⁻⁶+12∙2⁻⁶+...=14.45392

Uₜₒₜₐₗ=2Nε[12.1388(σ/R)¹²-14.45392(σ/R)⁶]

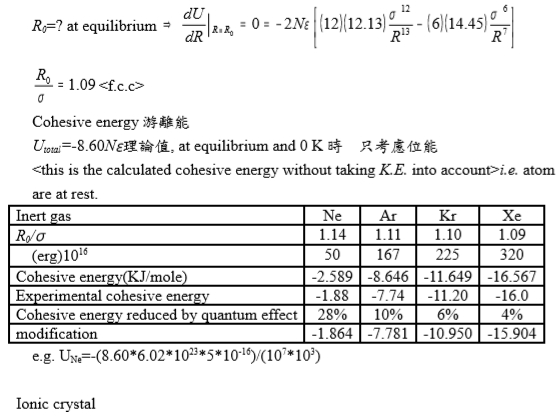
R₀=? at equilibrium dU/dR|_R=R₀=0=-2Nε[12.13(12σ¹² /R¹³)-14.45(6σ⁶/R⁷)]

R₀/σ=1.09

Cohesive energy游離能

U_total=-8.60N理論值, at equilibrium and 0 K時, 只考慮位能

K.E. into account>i.e. atom are at rest.

Inert gas	Ne	Ar	Kr	Xe
R0/	1.14	1.11	1.10	1.09
ε(erg)1016	50	167	225	320
Cohesive energy(KJ/mole)	-2.589	-8.646	-11.649	-16.567
Experimental cohesive energy	-1.88	-7.74	-11.20	-16.0
Cohesive energy reduced by quantum effect	28%	10%	6%	4%
modification	-1.864	-7.781	-10.950	-15.904

 

e.g. U_Ne=-(8.606.0210²³510^-16)/(10⁷10³)

 

Ionic crystal

Two common crystal structure: 1. NaCl(f.c.c.), 2. CsCl(b.c.c.)

What forces contribute to the crystal binding?

1. electrostatic force: coulomb’s force, attractive force.

2. exchange force: repulsive force due to the overlapping of electron orbits.

3. van der Waal’s force: dipole-to-dipole interaction效果約1%忽略之

Uₜₒₜₐₗ=½∑ᵢ ∑_j U_ij, energy includes(i)coulomb: ±q²/r_ij, (ii)exchange: λe^-rij/ρ

Uₜₒₜₐₗ=½∙2N∑_jU_ij=N∑_jU_ij=N∑_j(λe^-rij/ρ±q²/r_ij)

令r_ij=P_ijR, Uₜₒₜₐₗ=N∑_jλe^-rij/ρ-N∑_j(±1/P_ij)(q²/R), ∑_j(±1/P_ij)=Modelung constant

Uₜₒₜₐₗ=Nzλe^-R/ρ-N∑_j(±1/P_ij)(q²/R) , define α≡∑_j(±1/P_ij)=modelung constant

NaCl crystal(f.c.c.): pick Cl^- as a reference ion

Nearest ion: 6Na⁺, R₀

2^nd nearest ions: 12 Cl^-, √2R₀

3^rd nearest ion: 8 Na⁺, √3R₀

α=[6∙1⁻¹+12∙√2⁻¹²+8∙√3⁻¹+...]=1.747565

CsCl crystal(b.c.c.) : pick Cs^+- as a reference ion

Nearest ion: 8Cl^-, R₀=√3a/2

2^nd nearest ions: 6Cs+, R=a=2R₀/√3

3^rd nearest ion: … α=1.762675

Uₜₒₜₐₗ=Nzλe^-R/ρ-Nα(q²/R)

determination of , : characteristic force range

bulk modulus, B≡-VdP/dV, definition for a crystal of f.c.c. structure

V=2NR³ → dV=6NR²dR B=-2NR³dP/(6NR²dR)=-(R/3)(dP/dR)

dU=TdS-PdV=-PdV=-P6NR²dR at 0 K and R=R₀

P=-(1/6NR²)dU/dR, ⸫ dP/dR=-(1/6NR²)d²U/dR²+(1/3NR³)dU/dR

B=-(R/3)(dP/dR)=-(R/3)[-(1/6NR²)d²U/dR²+(1/3NR³)dU/dR]

=(1/18NR)d²U/dR²+(1/9NR²)dU/dR]

at equilibrium state, R=R₀ dU/dR=0, ⸫ B=(1/18NR)d²U/dR²|_R=R₀

Uₜₒₜₐₗ=Nzλe^-R/ρ-Nα(q²/R) → dU/dR=N[-zλe^-R/ρ/ρ+αq²/R²]=0, R₀²=ραq²/(zλe^-R/ρ)

d²U/dR²=N[zλe^-R/ρ/ρ²-2αq²/R³]|_R=R₀=N[αq²/ρR₀²-2αq²/R₀³]

→ B=(1/18NR₀)∙N[αq²/ρR₀²-2αq²/R₀³]=αq²/18R₀⁴(R₀/ρ-2)

→ R₀/ρ=18R₀⁴B/αq²+2, ⸫ ρ=R₀(18R₀⁴B/αq²+2)⁻¹

ex. NaCl B=2.4010¹¹, R₀=2.820Å, =1.747565, q=1.610^-19coul=4.810^-10 statcoulombs(1coul=310⁹ statcoulombs)

→ =0.321Å

 

U(R)=Nzλe^-R/ρ-Nα(q²/R)=N[zλe^-R₀/ρ-α(q²/R₀)]|_R=R₀,

dU/dR=N[-zλe^-R/ρ/ρ+αq²/R²]=0, R₀²e^-R/ρ=ραq²/(zλ) when R=R₀

U(R₀)=N[αq²ρ/R₀²-αq²/R₀]=Nαq²/R₀[ρ/R₀-1]