什麼是「陰謀論」?一件不可思議的事情發生了,令人瞠目結舌。很多人會說:如果沒有陰謀,這種事情根本不可能發生;現在發生了,它背後一定有陰謀在運作。這種推論類似於對超自然力量存在的推論:如果沒有超自然力量,這種事情根本不可能發生;現在發生了,它背後一定有超自然力量在運作。宗教信徒常主張的「智慧設計論」(intelligent design)便是這樣的邏輯。陰謀論與智慧設計論具有相同的邏輯結構。
一、陰謀論的邏輯結構
陰謀論者不認為關鍵事實能從正常人的行為自然產生,而必須訴諸想像中超越正常、隱藏幕後的組織運作才能理解。在這個意義上,陰謀也可以說是一種「超自然力量」,其邏輯結構如下:
- 前提1:如果沒有陰謀,事情不會發生
- 前提1a:如果事情發生,一定有陰謀
- 前提2:事情發生了
- 結論:有陰謀
前提1a是前提1依命題邏輯之「以否定後項來否定前項」(modus tollens)的法則而來。一旦前提1a確立,加上前提2的事實,則有陰謀的結論自然成立。這是「以肯定前項來肯定後項」(modus ponens)的演繹法。
這種推論的問題在於:即使陰謀真的會導致此事發生,但我們通常無法排除其它的原因。陰謀可以是事情發生的充分條件,但前提1以及前提1a卻把陰謀當成必要條件。
如果我們同意陰謀只能是充分條件,則陰謀論的推理方法變成這個樣子:
- 前提1b:如果有陰謀,事情一定會發生
- 前提2:事情發生了
- 結論:有陰謀
這個推理方法就不是演繹法了,它喚做「回溯推論法」(abduction)。
關於回溯推論法,請參考我的文章:〈回溯推論法、貝氏定理、及推理小說〉
回溯推論法的問題在於:第一,如果無法排除事情發生的其它可能原因,它便犯了「以肯定後項來肯定前項」的邏輯謬誤。第二,即使有陰謀,其實事情也不一定就會發生;換句話說,陰謀不但不必然是必要條件,也不必然是充分條件。
這兩個問題都牽涉到機率:如果事情發生有很多可能的原因,這些原因各佔多少機率?如果有陰謀不必然保證事情發生,那它會導致事情發生的機率是多少?
忽略機率——把「可能」當成「必然」——會讓回溯推論法歪樓而產生可笑的結論。福爾摩斯小說每篇一開始幾乎都是貝克街221B中福爾摩斯以回溯推論法逆推華生心思或客戶身分的場景。這些推理常令小說角色驚訝,但其實邏輯鬆懈,仔細思考就會發現它們都沒有考慮到上述的機率問題。在《跳舞的人》案件,福爾摩斯看了華生左手的虎口有白粉,就推論說他沒有打算投資金礦。從前提到結論之間共有五個環節,每個環節其實都有機率問題。柯南.道爾不讓華生去細究這些機率而讓他在了解環節之後大叫「這太簡單了!」純粹是為了製造喜劇效果而已。
二、渣男事件的貝氏分析
回到陰謀論。如果我們知道這些機率,那我們就可以算出有陰謀的機率是多少。這要用到奇妙的貝氏定理。
今天有渣男攀緣名流、惡行惡相,有恃無恐,而又金援充裕。很多人認為不可思議,推論其人背後必有陰謀集團指使撐腰。
要對這個陰謀論做貝氏分析,我們必須要先估計在這些事實曝光之前,究竟有陰謀集團運作的機率是多少?這就是所謂先驗機率,這個機率仰賴主觀信仰,其估計會因人而異。我們先假定這個機率為θ。
另外,我們也要估計有陰謀及沒有陰謀兩種理論之下的條件機率。我們依照陰謀論,假設陰謀之下產生這種渣男的機率非常高,但不是百分之百,而是0.99。這個機率是醫學檢定中「真陽性」的機率,資料科學則稱為「召回率」(recall),意思是所要檢定的機制(陰謀)運作時可以得到的成效。統計術語則稱之為檢定「強度」(power)。如果以「H1」標記陰謀論的假說,「+」標記經驗資料,則這裡召回率=Pr(+|H1)=0.99表示檢定強度極高了。
陰謀論另一個假設是:若無陰謀團體運作,產生這種渣男的機率非常低。我們姑且假設它的確很低,但不是零,而是0.05。這是醫學檢定中「偽陽性」的機率。如果用統計學的術語,它是在虛無假說(H0:無陰謀)之下觀察到經驗資料(渣男)或更極端事實的機率,也就是所謂「p值」:p=Pr(+|H0)。統計學習慣上以0.05為顯著水平,p<0.05代表可以在這個水平上拒絕虛無假說。設定p=Pr(+|H0)=0.05表示資料恰恰足夠到與「無陰謀」之虛無假說不相諧的程度。
這些假設雖然不比陰謀論那麼絕對,但已相當接近,也比較合乎現實。表列如下:
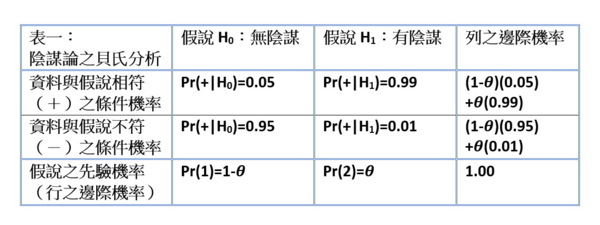
貝氏定理算得的陰謀為真的後驗機率為
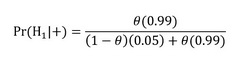
關於貝氏定理的計算,請參考我的文章:〈貝氏定理在生活中很有用,可是它到底怎麼算?〉
這個機率——真陽性的反機率——資料科學稱為「精密度」(precision),也就是事實發生之後,我們對陰謀論為真的機率判斷。這裡真陽性的機率(召回率)固定為Pr(+|H1)=0.99,而真陽性的反機率Pr(H1|+)是θ的函數,可以圖示如下:
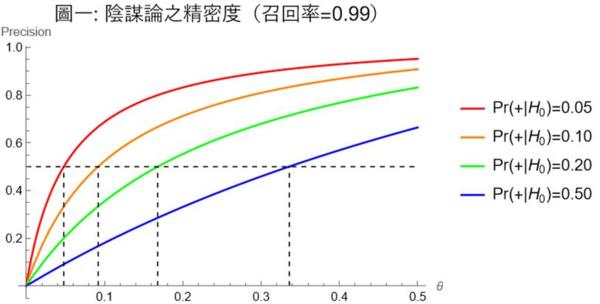
圖中除了顯示Pr(+|H0)=0.05假設之下陰謀論的精密度外(紅色曲線),也顯示了Pr(+|H0)=0.10、0.20、0.50假設之下的函數曲線。
從這個分析我們可以學到什麼?
首先,召回率對函數圖形的影響不大,所以分析時把召回率固定在0.99。
其次,即使在最合乎陰謀論的假設Pr(+|H0)=0.05之下,陰謀論的精密度也不必然很高。圖一的紅色曲線顯示,如果先驗機率小於0.048,陰謀論的精密度會小於0.5。這是說如果之前人們主觀上對陰謀存在的相信度低,那麼即使現在渣男行跡敗露了,陰謀論為真的機率還不到0.5!其實,對於主觀上認為有陰謀的機率微乎其微(θ→0)的人,後驗機率也是接近於零的。只有在先驗機率高到0.5時,後驗機率才會接近百分之百。
再來,當Pr(+|H0)越高時,要讓精密度超過0.5的先驗機率也必須越來越高。這是說如果渣男的行為在沒有陰謀集團存在時也甚有可能,則除非你本來就很相信陰謀論,否則即使渣男曝光了,幕後真有陰謀的機率也不會很高。以Pr(+|H0)=0.50(藍色曲線)為例,必須要你的主觀先驗機率超過0.34,後驗機率才會超過0.5;而且即使先驗機率達到0.5,後驗機率也不過是0.66。
三、信者恆信,不信者恆不信?
總而言之,貝氏分析的結論雖然簡單說不外是「信者恆信,不信者恆不信」,但它釐清了很多一般人不一定清楚的假設,也給了我們較精確的估計。
做為一個政治學者,如果今天有陌生臉友來跟我討論Gadamar的哲學詮釋學,我可能會留意,因為我嘗試讀過,覺得很難懂。我可能會考驗他是不是真懂,但要我懷疑他是在某項陰謀之下來找我蹭交情,這還真要極大的「信仰跳躍」。
即使今天他對女友施暴,證明是渣男,然後又抖出了他攀緣名流等事實,要因此判定他背後有陰謀集團指使,還是要考慮這些事實在沒有陰謀的情況下有多大的可能性。渣男人人厭之,但因此就認為陌生人來接近你必有陰謀,就避之唯恐不及,這樣的人際關係,恐怕不是一個健康的社會所樂見的。



