均衡解的安定分析:
需求函數:Qᴅ=a-bP, a, b>0
供給函數:Qₛ=-α+βP, α, β>0
均衡價格P=(a+α)/(b+β).....(1) , 均衡交易量Q=a-b∙(a+α)/(b+β)=(aβ-bα)/(b+β).....(2) only if b+β≠0
但是b+β≠0的條件下有三種例外:
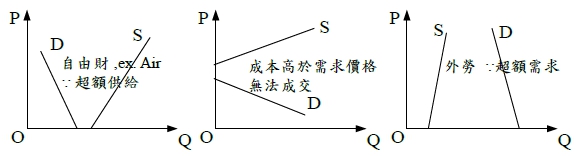
安定分析: 分析價格一旦離開均衡點後是否會恢復均衡的問題
瓦拉斯均衡安定的必要條件: 當供需失衡偏離均衡點E時, 會發生超額需求或超額供給, 而價格的變動會使超額需求或超額供給的變動減小, 使供需重回到均衡點E; 例如如下圖超額需求發生, 價格上漲,使超額需求量減少, 價格又慢慢回去均衡價格P。超額供給發生時亦然。數學表示如下
超額需求函數 E(P)=D(P)-S(P), dE(P)/dP=E(P)=D(P)-S(P)<0
ex. E(P)=D(P)-S(P)=a-bP-(-α+βP)=a+α-(b+β)P, E(P)=-(b+β)<0
馬夏爾均衡安定的必要條件: 當供需失衡偏離均衡點E時, 會發生超額需求價格變動或超額供給價格變動, 而產量的變動會使超額需求價格變動或超額供給價格變動減小, 使供需重回到均衡點E; 例如如下圖超額需求價格變動發生, 產量上升,使超額需求價格變動量減少, 產量又慢慢回去均衡價格Q*。超額供給價格變動發生時亦然。數學表示如下:
超額需求價格函數 F(Q)=D⁻¹(Q)-S⁻¹(Q), dF(Q)/dQ=F(Q)=D⁻¹(Q)-S⁻¹(Q)<0
蛛網理論, cobweb model:
適用時機: 是用於生產時間存在落差的產業中,例如農產品業:種稻,養豬,養雞..., 教育業(人才培育)
基本假設: 起初市價P₀, 當Qd>Qₛ則P會上升;當Qd<Qₛ則P會下降,
因此本期供給量視上一期的價格而決定→ Qₜs=f(Pₜ₋₁)且呈正相關;
本期需求量視現在(本期)的價格而決定→ Qₜd=f(Pₜ)且按供需法則呈負相關
P₀下,市場存在超額供給,使P₀ ↓
P₁下,市場存在超額需求,使P₁ ↑ .....直到均衡點P為止
蛛網理論以順時鐘方向趨向均衡, 蛛網理論之安定條件為供給曲線斜率必須大於需求曲線的斜率絕對值, 即 ms > |md| 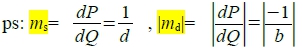
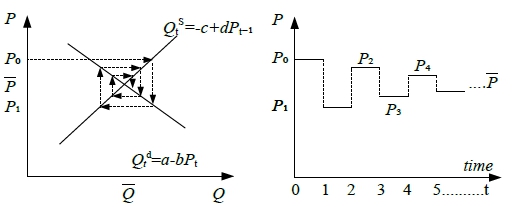
線性一階差分方程式Linear 1st-order antonomous difference equation
yₜ=ayₜ₋₁+b, t=0,1,2,…
t=0, y1=ay0+b
t=1, y2=ay1+b=a(ay0+b)+b=a2y0+b(1+a)
t=2, y3=ay2+b=a(a2y0+b(1+a))+b=a3y0+b(1+a+a2)
...
yₜ=aᵗy₀+b(1+a+a2+...+at-2+at-1)
, 1+a+a2+...+at-2+at-1=(1-aᵗ)/(1-a) if a≠1 or 1+a+a2+...+at-2+at-1=t if a=1
Qₜs=f(Pₜ₋₁)且呈正相關 → Qₜs=-c+dPₜ₋₁, c,d>0
Qₜd=f(Pₜ)且按供需法則呈負相關→ Qₜd=a-bPₜ, a,b>0
Qₜd=Qₜs => a-bPₜ=-c+dPₜ₋₁ => Pt=(-d/b)Pₜ₋₁+(a+c)/b......線性一階差分方程式(7)
P₁=(-d/b)P₀ +(a+c)/b
P₂=(-d/b)P₁ +(a+c)/b=(-d/b)[(-d/b)P₀ +(a+c)/b]+(a+c)/b=(-d/b)²P₀ +(a+c)/b[(-d/b)+1]
P₃=(-d/b)P₂ +(a+c)/b=...=(-d/b)³P₀ +(a+c)/b[(-d/b)²+(-d/b)+1]
…
Pt=(-d/b)ᵗP₀ +(a+c)/b[(-d/b)ᵗ⁻¹+(-d/b)ᵗ⁻²+...+(-d/b)²+(-d/b)+1]
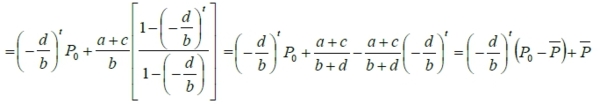
When steady state, Pt=Pₜ₋₁=P, 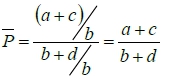
(7)式的均衡解: Pt=(-d/b)ᵗ(P₀-P)+P, P=(a+c)/(b+d)
另解: Pt=(-d/b)Pₜ₋₁+(a+c)/b 先解標準式 Pt+(d/b)Pₜ₋₁=0的一般解, Ptᴳ
令Ptᴳ=kAᵗ 代入原式解A → kAᵗ+(d/b)kAᵗ⁻¹=0 → kAᵗ⁻¹(A+d/b)=0 ⸫A=-d/b
Ptᴳ=k(-d/b)ᵗ 然後再解 Pt=(-d/b)Pₜ₋₁+(a+c)/b的特殊解, PtS → 令PtS=B 代入解B
B=(-d/b)B+(a+c)/b → B=(a+c)/(b+d)=PtS ⸫解為Ptᴳ+ PtS=k(-d/b)ᵗ+(a+c)/(b+d)
若已知P₀為起始值 → P₀=k(-d/b)⁰+(a+c)/(b+d) → k= P₀-(a+c)/(b+d) 因此最後解為
[P₀-(a+c)/(b+d)](-d/b)ᵗ+(a+c)/(b+d)
討論安定性:
a. 若|-d/b|<1, 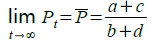 =正常數, 為安定解; |-d/b|<1 → |-1/b|<1/d → mₛ > |md|
=正常數, 為安定解; |-d/b|<1 → |-1/b|<1/d → mₛ > |md|
b. 若|-d/b|=1, 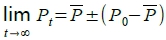 , 為非安定解(循環解)
, 為非安定解(循環解)
c. 若|-d/b|>1, 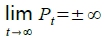 , 為非安定解(發散解)
, 為非安定解(發散解)


