Chapter 5 Auxiliary Function

dU=TdS- PdV, U=U(S,V); dS=dU/T+(P/T)dV, S=S(U,V) 操作變數不方便,改成方便操作的壓力、體積、溫度的變數,需用何種函數?

通常量測上用壓力和溫度,理論推導用溫度與體積

Energy function def: A≡U-TS, H≡U+PV, G≡H-TS 目的:將2nd law轉變形式來看

微分式

dH=dU+PdV+VdP=TdS-PdV+PdV+VdP=TdS+VdP, H(S,P)

dA=dU-TdS-SdT=TdS-PdV-TdS-SdT=-SdT-PdV, A(T,V)

dG=dH-TdS-SdT=TdS+VdP-TdS-SdT=-SdT+VdP, G(T,P)

利用4個能量函數的微分式座運算處理:

dU=TdS- PdV, dH=TdS+VdP, dA=-SdT-PdV, dG=-SdT+VdP

H, Enthalpy H≡U+PV

等壓過程, dHₚ=TdS+VdP=TdSₚ=δQₚ

state 1 → state 2 ∆H=H₂-H₁=(U₂-U₁)+(P₂V₂-P₁V₁),

at constant P, ∆Hₚ=∆U+P∆V=∆Qₚ-∆W+P∆V →∆Hₚ=∆Qₚ, ∆H=進入或離開的熱(焓)

A, Helmholtz free energy A≡U-TS

state 1 → state 2 ∆A=A₂-A₁=(U₂-U₁)-(T₂S₂-T₁S₁),

at const T, ∆A_ᴛ=(U₂-U₁)-T(S₂-S₁)=∆U-T∆S=∆Q-∆W-T∆S 因此, ∆A_ᴛ+∆W=∆Q-T∆S

⸪ ∆Q≤∆Qᵣₑᵥ=T∆S → ∆Q-T∆S≤0 ⸫∆A_ᴛ+∆W≤0 → ∆A_ᴛ≤-∆W

i.e. ∆A+T∆Sₚᵣₒ_ᵈ=-∆W → dA+TdSᵢᵣᵣₑᵥ=-δW

if constant V, δW=PdV=0 ⸫ dA_ᴛ,ᴠ+TdSᵢᵣᵣₑᵥ=0 under constant T and V,

dA_ᴛ,ᴠ= -TdSᵢᵣᵣₑᵥ≤0 (⸪2^nd law: dSᵢᵣᵣₑᵥ≥0) A↓, A_ᴛ,ᴠ= Aₘᵢₙ in equil.

Ex. 在固定溫度和體積的固體昇華成氣體,看能量與氣體粒子的關係

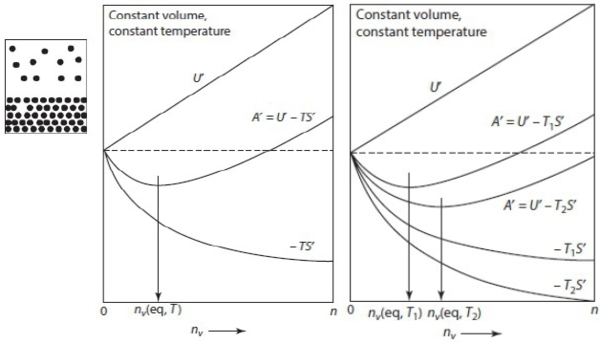
If P<Pₑ_զ → nᵥ< nᵥ,ₑ_զ

∆S_熱儲=-Q/T...(1), ∆S_gas=+(Q/T)+∆Sₚᵣₒ_ᵈ...(2), (1)+(2) ∆S_total=∆Sₚᵣₒ_ᵈ=∆Sᵢᵣᵣₑᵥ

for gas at constant T and V, ∆A_ᴛ,ᴠ+T∆Sₚᵣₒ_ᵈ=0 → ∆A_ᴛ,ᴠ=-T∆Sₚᵣₒ_ᵈ → ∆A_ᴛ,ᴠ≤0

G, Gibbs free energy G≡H-TS

state 1 → state 2 ∆G=G₂-G₁=(H₂-H₁)-(T₂S₂-T₁S₁)=(U₂-U₁)+(P₂V₂-P₁V₁)-(T₂S₂-T₁S₁),

at const T and P, ∆G_ᴛ,ᴩ=(U₂-U₁)+P(V₂-V₁)-T(S₂-S₁)=∆U+P∆V-T∆S=∆Q-∆W+P∆V-T∆S i.e.∆W=P∆V+∆W → ∆G_ᴛ,ᴩ=∆Q-∆W-T∆S

⸪ ∆Q≤∆Qᵣₑᵥ=T∆S → ∆Q-T∆S≤0 ⸫∆G_ᴛ,ᴩ+∆W≤0 → ∆G_ᴛ,ᴩ≤-∆W

i.e. ∆G_ᴛ,ᴩ+T∆Sₚᵣₒ_ᵈ=-∆W if no other work, ∆W=0 ⸫ ∆G_ᴛ,ᴩ+T∆Sₚᵣₒ_ᵈ=0,

∆G_ᴛ,ᴩ= -T∆Sᵢᵣᵣₑᵥ≤0 (⸪2^nd law: ∆Sᵢᵣᵣₑᵥ≥0) G↓,

if ∆G_ᴛ,ᴩ<0, span="">state 1 → state 2自然發生, 而且G_ᴛ,ᴩ= Gₘᵢₙ at equilibrium point.

Summary: 如何判斷變化是否發生和平衡的條件

2^nd law: dS_ᴜ,ᴠ≥0, 達平衡時S_ᴜ,ᴠ=Sₘₐₓ 而且dS_ᴜ,ᴠ=0

dU_S,ᴠ≤0, U_S,ᴠ=Uₘᵢₙ; dH_S,ᴩ≤0, H_S,ᴩ=Hₘᵢₙ; dA_ᴛ,ᴠ≤0, A_ᴛ,ᴠ=Aₘᵢₙ; dG_ᴛ,ᴘ≤0, G_ᴛ,ᴘ=Gₘᵢₙ

將第二定律entropy增加的條件轉換成能量下降的條件,方便操作!

能量函數定義: A≡U-TS, H≡U+PV, G≡H-TS 須記熟

微分式

dU=TdS- PdV, U(S,V)

dH=TdS+VdP, H(S,P)

dA=-SdT-PdV, A(T,V)

dG=-SdT+VdP, G(T,P)

Section 6&7 chemical work(potential)成分變化 G=G(T,P,n_i,n_j,…)

dG=(∂G∕∂T)_ᴘ,nᵢ,...dT+(∂G∕∂P)_ᴛ,nᵢ,...dP+(∂G∕∂nᵢ)_{ᴛ,ᴘ,nj,...}dnᵢ+.. 若組成物莫耳數保持一定 dG=(∂G∕∂T)_ᴘdT+(∂G∕∂P)_ᴛdP

def: (∂G∕∂nᵢ)_{ᴛ,ᴘ,nj,...}=μᵢ化學勢 dG=-SdT+VdP+Σμᵢnᵢ ,

i.e. (∂G∕∂nᵢ)_{ᴛ,ᴘ,nj,...}=(∂A∕∂nᵢ)_{ᴛ,ᴘ,nj,...}=(∂H∕∂nᵢ)_{ᴛ,ᴘ,nj,...}=(∂U∕∂nᵢ)_{ᴛ,ᴘ,nj,...}

熱力學的數學推導(係數關係)

dU=TdS- PdV=(∂U∕∂S)ᵥdS+(∂U∕∂V)ₛdV, T=(∂U∕∂S)ᵥ=(∂H∕∂S)ₚ

dH=TdS+VdP=(∂H∕∂S)ₚdS+(∂H∕∂P)ₛdP, S=-(∂A∕∂T)ᵥ=-(∂G∕∂T)ₚ

dA=-SdT-PdV=(∂A∕∂T)ᵥdT+(∂A∕∂V)_ᴛdV, P=-(∂U∕∂V)ₛ=-(∂A∕∂V)_ᴛ

dG=-SdT+VdP=(∂G∕∂T)ₚdT+(∂G∕∂P)_ᴛdP, V=(∂H∕∂P)ₛ=(∂G∕∂P)_ᴛ

Maxwell relation :

if Z=Z(x,y), dZ=(∂Z∕∂x)_ydx+(∂Z∕∂y)_xdy=Ldx+Mdy and (∂L∕∂y)_x=(∂M∕∂x)_y

∴(∂T∕∂V)ₛ=-(∂P∕∂S)ᵥ, (∂T∕∂P)ₛ=(∂V∕∂S)ₚ, (∂S∕∂V)_ᴛ=(∂P∕∂T)ᵥ, -(∂S∕∂P)_ᴛ=(∂G∕∂T)ₚ

Derived equations

Ex-1. ideal gas: U=U(T), (∂U∕∂V)_ᴛ=0, (∂U∕∂P)_ᴛ=0

pf: dU=TdS- PdV

(∂U∕∂V)_ᴛ=T(∂S∕∂V)_ᴛ-P=T(∂P∕∂T)ᵥ-P=T(R/V)-P=0,

(∂U∕∂P)_ᴛ=T(∂S∕∂P)_ᴛ-P(∂V∕∂P)_ᴛ=-T(∂V∕∂T)ₚ-P(-RT/P²)=-T(R/P)+RT/P=0

or (∂U∕∂S)_ᴛ=T-P(∂V∕∂S)_ᴛ=T-P(∂T∕∂P)ᵥ=T-P (R/V)=0 所以U為T的函數, 與壓力,體積, S均無關

Ex-2. ideal gas: H=H(T), (∂H∕∂V)_ᴛ=0, (∂H∕∂P)_ᴛ=0

pf: dH=TdS+VdP

(∂H∕∂V)_ᴛ=T(∂S∕∂V)_ᴛ+[∂(VdP)/∂V]_ᴛ=T(∂P∕∂T)ᵥ-P=T(R/V)-P=0

⸪PV=RT → PdV+VdP=0 ⸫-P=(VdP)/dV

(∂H∕∂P)_ᴛ=T(∂S∕∂P)_ᴛ+V=-T(∂V∕∂T)ₚ+V=-T(R/P)+V=0

or (∂U∕∂S)_ᴛ=T+V(∂P∕∂S)_ᴛ=T-V(∂T∕∂P)ᵥ=T-P (R/V)=0 所以H為T的函數

ratio relation z=z(x, y), (∂x∕∂y)_z(∂y∕∂z)_x(∂z∕∂x)_y=-1

pf: dz=(∂z∕∂x)_ydx+(∂z∕∂y)_xdy → dz/[(∂z∕∂x)_y]=dx+(∂z∕∂y)_xdy/[(∂z∕∂x)_y]=dx+(∂z∕∂y)_x(∂x∕∂z)_ydy ...(a)

x=x(y, z), dx=(∂x∕∂y)_zdy+(∂x∕∂z)_ydz ...(b), 比較(a),(b) → (∂x∕∂y)_z=-(∂z∕∂y)_x(∂x∕∂z)_y

利用倒數關係, (∂x∕∂y)_z(∂y∕∂z)_x(∂z∕∂x)_y=-1

Ex.-3 TdS equations

dS≡δQᵣₑᵥ/T → δQ=TdS → ∆Q=∫_₁^²δQ=∫_₁^²TdS

δQ=TdS=(?)dT+(?)dV 1^st TdS equation→ TdS=f(T,V)

δQ=TdS=(?)dT+(?)dP 2^nd TdS equation→ TdS=f(T,P)

δQ=TdS=(?)dP+(?)dV 3^rd TdS equation→ TdS=f(P,V)

1^st TdS equation S=S(T,V) → dS=(∂S∕∂T)ᵥdT+(∂S∕∂V)_ᴛdV

TdS=δQ=cᵥdT i.e. cᵥ=(δQᵣₑᵥ/dT)ᵥ →cᵥ=T∙(∂S/∂T)ᵥ=(∂U/∂T)ᵥ ⸪dU_ᵛ=δQ_ᵛ, c_ᵛ= δQᵥ/dT=(∂U/∂T)ᵥ

→dS=(cᵥ∕T)dT+(∂P∕∂T)ᵥdV→ dS=(cᵥ∕T)dT+(α∕β)dV

⸪P=P(T,V) its ratio relation, (∂P∕∂T)ᵥ(∂T∕∂V)ₚ(∂V∕∂P)_ᴛ=-1

→ (∂P∕∂T)ᵥ=-(∂V∕∂T)ₚ/(∂V∕∂P)_ᴛ=-αV/-βV=α/β

i.e. expansion coeff. α=(1/V)(∂V∕∂T)ₚ, compressibility β=(-1/V)(∂V∕∂P)_ᴛ

1^st TdS equation→ TdS=f(T,V)=cᵥdT+(αT∕β)dV

state 1(T₁,V₁) → state 2(T₂,V₂) ∆Q=∫_₁^²δQ=∫_₁^²TdS=∫_ᴛ₁^ᵀ²cᵥdT+∫_ᴠ₁^ᴠ²(αT∕β)dV

2^nd TdS equation S=S(T,P) → dS=(∂S∕∂T)ₚdT+(∂S∕∂P)_ᴛdP

δQₚ=TdSₚ=c_ₚdT , ⸪c_ₚ=(δQ/dT)ₚ ⸫(∂S∕∂T)ₚ=c_ₚ/T and (∂S∕∂P)_ᴛ=-(∂V∕∂T)ₚ=-αV

dS=(∂S∕∂T)ₚdT+(∂S∕∂P)_ᴛdP=(c_ₚ/T)dT-αVdP→TdS=c_ₚdT-αVTdP

Ex-4 Gibbs-Helmholtz equation: 定壓[d(∆G/T)/dT]_ₚ=-∆H/T², 已知G(T) 如何計算H(T)

G≡H-TS →[∂(G/T)/∂T]_ₚ=[∂(H/T)/∂T]_ₚ-(∂S∕∂T)ₚ=[T(∂H/∂T)_ₚ-H]/T²-c_ₚ/T=c_ₚ/T-H/T²-c_ₚ/T=-H/T²

i.e. df(y/x)=(xdy-ydx)/x²

同理[∂(G₂/T)/∂T]_ₚ-[∂(G₁/T)/∂T]_ₚ=-H₂/T²-(-H₁/T²) → [∂(∆G/T)/∂T]_ₚ=-∆H/T²

experimental data: G vs. T plot transform to G/T vs. 1/T plot

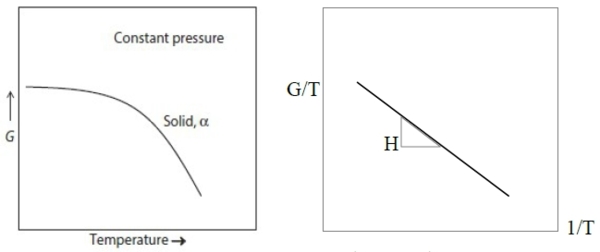
[∂(∆G/T)/∂T]_ₚ=-∆H/T² → [∂(∆G/T)/∂(1/T)]_ₚ=∆H

Ex-5 Helmholtz-internal energy equation: 定容[∂(∆A/T)/∂T]_ᵥ=-∆U/T² 已知A(T) 如何計算U(T)

A≡U-TS, 同理[∂(A/T)/∂T]_ᵥ=[∂(U/T)/∂T]ᵥ_-(∂S∕∂T)ᵥ=[T(∂U/∂T)ᵥ_-U]/T²-cᵥ_/T=cᵥ_/T-U/T²-cᵥ_/T=-U/T²

Ex.-6 _{c≡δQ/dT ,} c_ₚ=(δQ/dT)ₚ, cᵥ=(δQ/dT)ᵥ

eq. 2-8, cₚ-cᵥ=(∂U∕∂V)_ᴛ(∂V∕∂T)ₚ+P(∂V∕∂T)ₚ=(∂V∕∂T)ₚ[P+(∂U∕∂V)_ᴛ]轉換成可量的物理量

⸪dA=-SdT-PdV ⸫(∂A/∂V)_ᴛ=-P, and A≡U-TS (∂A/∂V)_ᴛ=(∂U/∂V)_ᴛ-T(∂S/∂V)_ᴛ=(∂U/∂V)_ᴛ-T(∂P/∂T)ᵥ

→ -P=(∂U/∂V)_ᴛ-T(∂P/∂T)ᵥ代入eq. 2-8, cₚ-cᵥ=T(∂V∕∂T)ₚ(∂P/∂T)ᵥ

⸪(∂P∕∂T)ᵥ(∂T∕∂V)ₚ(∂V∕∂P)_ᴛ=-1 → (∂P∕∂T)ᵥ=-(∂V∕∂T)ₚ/(∂V∕∂P)_ᴛ=-αV/-βV=α/β

⸫cₚ-cᵥ=T(∂V∕∂T)ₚ(∂P/∂T)ᵥ=-T(∂V∕∂T)²ₚ/(∂V∕∂P)_ᴛ=α²VT/β

i.e. expansion coeff. α=(1/V)(∂V∕∂T)ₚ, compressibility β=-(1/V)(∂V∕∂P)_ᴛ

Ex. Al=26.98 g/mole, 求cᵥ=? (c_{ₚ=24.36 J/Kmole,} T=298K, α=7.3510⁻⁵ /K, β=1.210⁻⁶ /atm, ρ=2.7 g/cm³)

V=26.98/2.7≈10 cm³/mole=10⁻² l/mole, cᵥ=c_ₚ-(α²VT/β_{)=23.13 J/Kmole}

_{Ex. adiabatic thermoelastic effect: 利用施加突然的壓力轉成熱使溫度升高,做非破壞的缺陷檢測}

_{Al₂O₃ 施加sudden ∆P=500 MPa, 求∆T=? (Given:} c_{ₚ=80 J/Kmole,} T=298K, α=2.210⁻⁵ /K, V=25.6 cm³/mole)

⸪_{sudden loading ∆P and no heat dissipation→adiabatic and heat make T increase}

⸫(∂T/∂P)_ₛ=? (∂T∕∂P)ₛ(∂P∕∂S)_ᴛ(∂S∕∂T)ₚ=-1 and cᵥ=T∙(∂S/∂T)ᵥ, c_ₚ=T(δS/dT)ₚ=(δH/dT)ₚ

(∂S∕∂P)_ᴛ=-(∂V∕∂T)ₚ=-αV → (∂T/∂P)_ₛ=-(∂S∕∂P)_ᴛ/(∂S∕∂T)ₚ= αV/(c_ₚ/T)=αVT/c_ₚ

→ ∫_ᴛ₁^ᵀ²dT/T=∫_ᴩ₁^ᴾ₂(αV/c_ₚ)dP=αV/c_{ₚ(P₂-P₁)}, T₂=299K, _∆T=1K

_補充: Dehoff ch-4, pp.51-71 general strategy for deriving thermodynamic equations

_{e.g. 5-11} (∂T/∂P)_ₛ=? 2^nd TdS equation TdS=c_ₚdT-αVTdP ⸪dS=0 ⸫(∂T/∂P)_ₛ=αVT/c_ₚ

概念1: 溫度和壓力是實作上最容易操作的變數,自變數以T, P表示,其他變數(V, S, U, H, A, G)都轉換成以自變數T, P表示的函數Z=Z(T, P) → dZ=(?)dT+(?)dP

V=V(T,P) → dV=(∂V∕∂T)ₚdT+(∂V∕∂P)_ᴛ dP=αVdT- βVdP

S=S(T,P) → dS=(∂S∕∂T)ₚdT+(∂S∕∂P)_ᴛdP=(c_ₚ/T)dT-αVdP i.e. (∂S∕∂P)_ᴛ=-(∂V∕∂T)ₚ=-αV

dU=TdS- PdV=T[(c_ₚ/T)dT-αVdP]-P[αVdT- βVdP]=(c_ₚ-αPV)dT+V(βP-αT)dP

dH=TdS+VdP=T[(c_ₚ/T)dT-αVdP]+VdP=c_ₚdT+V(1-αT)dP

dA=-SdT-PdV=-SdT-P(αVdT- βVdP)=-(S+αPV)dT+βPVdP

dG=-SdT+VdP

基礎公式:

dV=αVdT- βVdP, dS=(c_ₚ/T)dT-αVdP, dU=(c_ₚ-αPV)dT+V(βP-αT)dP,

dH=c_ₚdT+V(1-αT)dP, dA=-(S+αPV)dT+βPVdP, dG=-SdT+VdP

概念2:Z=Z(x,y), dZ=Mdx+Ndy 將dx=X_ᴛdT+XₚdP, dy=Y_ᴛdT+YₚdP代入dZ

dZ=M(X_ᴛdT+XₚdP)+N(Y_ᴛdT+YₚdP)=(MX_ᴛ+NY_ᴛ)dT+(MXₚ+NYₚ)dP

再比較dZ=Z_ᴛdT+ZₚdP解M, N

習題練習:

5-1, 5-2, 5-9 S=S(P,V) dS=MdP+NdV=MdP+N(αVdT-βVdP)= NαVdT+(M-NβV)dP

與dS=(c_ₚ/T)dT-αVdP 比較, NαV=c_ₚ/T, M-NβV=-αV ⸫M=βc_ₚ/α_T- αV, N=c_ₚ/αV_T,

(∂S∕∂P)ᵥ=M=βc_ₚ/α_T- αV=βcᵥ_/α_T, (∂S∕∂V)ₚ=N=c_ₚ/αV_T, i.e. c_ₚ-cᵥ=α²V_T/β

(∂P∕∂V)ₛ=-N/M=-(c_ₚ/αV_T)/(βcᵥ_/α_T)=-c_ₚ/βcᵥV

3^rd TdS equation: S=S(P,V) TdS=(c_ₚ/αV)dV+(βcᵥ_/α)dP

5-3, 5-4 A=A(P,V) dA=MdP+NdV=MdP+N(αVdT-βVdP)= NαVdT+(M-NβV)dP

與dA=-(S+αPV)dT+βPVdP 比較, NαV=-(S+PVα)_, M-NβV=PVβ

⸫M=-βS_/α, N=-(S+PVα)_/αV, (∂A∕∂P)ᵥ=M=-βS_/α, (∂A∕∂V)ₚ=N=-(S+PVα)_/αV

dA=(-βS_/α)dP-[(S+PVα)_/αV]dV

5-5, 5-6 H=H(S,V) dH=MdS+NdV=M(c_ₚ/TdT-VαdP)+N(αVdT-βVdP)=(Mc_ₚ/T+NαV)dT-(MVα+βNV)dP, 與dH=c_ₚdT+V(1-αT)dP比較, Mc_ₚ/T+NαV=c_{ₚ, M}α₊β_N=αT-1

⸫M=T(1+αV_/βcᵥ), N=-c_ₚ/βcᵥ, (∂H∕∂S)ᵥ=M=T(1+αV_/βcᵥ), (∂H∕∂V)ₛ=N=-c_ₚ/βcᵥ

dH=T(1+αV_/βcᵥ)dS-(c_ₚ/βcᵥ)dV

5-8 S=S(T,P) → dS=(∂S∕∂T)ₚdT+(∂S∕∂P)_ᴛdP=(c_ₚ/T)dT-αVdP i.e. (∂S∕∂P)_ᴛ=-(∂V∕∂T)ₚ=-αV

⸪dS=0 ⸫(∂T/∂P)_ₛ=αVT/c_ₚ

5-10. dG=-SdT+VdP→ (∂G∕∂P)_ᴛ=V → [∂(∂G∕∂P)_ᴛ/∂P]_ᴛ=(∂V∕∂P)_ᴛ

dA=-SdT-PdV→ (∂A∕∂V)_ᴛ=-P → [∂(∂A∕∂V)_ᴛ/∂V]_ᴛ=-(∂P∕∂V)_ᴛ ⸫(∂²G∕∂P²)_ᴛ=-1/(∂²A∕∂V²)_ᴛ

5-7.

(∂c_ₚ∕∂P)_ᴛ=[∂(∂H∕∂T)ₚ∕∂P]_ᴛ=[∂(∂H∕∂P)_ᴛ∕∂T]ₚ=[∂(V-αVT)∕∂T]ₚ=(∂V∕∂T)ₚ-[αV+αT(∂V∕∂T)ₚ+VT(∂α∕∂T)ₚ]

i.e. dV=αVdT- βVdP, dH=c_ₚdT+V(1-αT)dP

→ (∂c_ₚ∕∂P)_ᴛ=(∂V∕∂T)ₚ-[αV+αT(∂V∕∂T)ₚ+VT(∂α∕∂T)ₚ]=-[α²+(∂α∕∂T)ₚ]VT

application to monatomic ideal gas, δQ=TdS → ∆Q=∫_₁^²δQ=∫_₁^²TdS

p.s. cᵥ=3R/2, cₚ=5R/2, γ=5/3, cₚ-cᵥ=R, α=1/T, β=1/P,

U(T) and H(T)與P,V無關, dU=cᵥdT, dH=cₚdT

DeHoff Ex.4-7 1 mole monatomic ideal gas changes from state 1(T₁=298K, P₁=1 atm) to state 2(T₂=298K, P₂=1000 atm), ask ∆S=?

Sol: S=S(T,P) → dS=(∂S∕∂T)ₚdT+(∂S∕∂P)_ᴛdP=(c_ₚ/T)dT-αVdP

∆S=∫_₁^²dS=∫_ᴩ₁^ᴾ₂-αVdP=-∫_ᴩ₁^ᴾ₂(V/T)dP=-∫_ᴩ₁^ᴾ₂(R/P)dP=Rln(P₁/P₂)=-57.4 J/K

Ex.4-10 Ask ∆Q=? by following process. 1. reversible isothermal P₁(5 atm) → P₂(1 atm). 2. reversible isobaric V₁ → V₂. 3. reversible isochoric T₁ → T₂.

Sol: 1. S=S(T,P) ⸫TdS=c_ₚdT-αVTdP →∆Q_ᴛ =∫_₁^²TdS=∫_ᴩ₁^ᴾ₂-αTVdP=-∫_ᴩ₁^ᴾ₂(RT/P)dP=RTln(P₁/P₂)

2. S=S(P,V) ⸫TdS=(c_ₚ/αV)dV+(βcᵥ_/α)dP→∆Q_ₚ=∫_₁^²TdS=∫_ᴠ₁^ᴠ²(c_ₚ/αV)dV=∫_ᴠ₁^ᴠ²(c_ₚT/V)dV= c_{ₚTln(V₂/V₁)=5RTln(V₂/V₁)/2}

3. S=S(T,V) ⸫TdS=f(T,V)=cᵥdT+(αT∕β)dV→∆Qᵥ=∫_₁^²TdS=∫_ᴛ₁^ᵀ²cᵥdT=cᵥ(T₂-T₁)

Ex.4-11 1 mole monatomic ideal gas changes from state 1(T₁=273K, P₁=1 atm) to state 2(T₂=?K, P₂=0.5 atm) by the change of V=22.4P , ask ∆Q=? T₂=?

Sol: ideal gas follow PV=RT, V=22.4P=RT/P → RT=22.4P² ⸫T₂= 22.4P₂²/R=68.2K

∆Q=∫_₁^²TdS=∫_ᴛ₁^ᵀ²c_ₚdT -∫_ᴩ₁^ᴾ₂αTVdP=c_ₚ(T₂-T₁)-∫_ᴩ₁^ᴾ₂22.4PdP=c_ₚ(T₂-T₁)-11.2(P₂²-P₁²)