
4月14日,有17位專家學者便在medRxiv網站上發表了在加州聖克拉拉郡做的抗體檢測研究。這個網站所發表的都是未經同儕審查的初步報告(preprint),這項研究之所以受到特別注意是因為它的作者中有一位大大有名的史丹福大學醫學院教授,近年來以批判傳統頻率學派統計檢定方法聞名的John P. A. Ioannidis。研究結果發現:經過加權之後盛行率的估計值是2.8%,意味聖克拉拉郡有54,000居民受過病毒感染,是當時該郡官方確診數1,000的54倍!但這項研究因為使用的是自願樣本,不是隨機抽樣,受到很多批評,連帶使得Ioannidis的聲譽受到影響。
值得注意的是:(1)這研究的樣本係從市場研究公司宣稱能代表全郡居民的數據庫為母體分層隨機抽樣。最初抽中的1,952人有1,702人同意受測,但最後只有863成功樣本數。這863人中有13%有發燒兼咳嗽症狀,9%發燒兼呼吸短促,6%喪失味覺或嗅覺。(2)研究所使用的檢測試劑,其敏感性為82.7%(信心區間76.0%-88.4%),特異性為99.5%(信心區間99.2%-99.7%)。
https://jamanetwork.com/journals/jama/fullarticle/2766367
然而美國CDC在5月23日發出一份【關於新冠病毒抗體檢測的臨時性指導方針】。這份文件旨在說明血清抗體檢測缺乏精確性、警告各界不要輕易以檢測的結果作為解封、復工決定的依據。文件並提出一些改進抗體檢測精密性的方法,這包括提高檢測試劑的特異性以及以「二採陽」作檢定結果的最終判斷。
CDC這份文件以實例說明抗體檢測之「陽性預測值」(positive predictive value, PPV)與病毒盛行率(prevalence)的密切關係,指出當特異性、盛行率都不夠高時,PPV可能甚低。
所謂PPV就是數據科學的「精密性」(precision)。我們知道醫學檢測的品質有特異性(specificity)與敏感性(sensitivity)兩個基本面向。特異性是真陰性的比例,也就是未帶原者檢測陰性的比例。敏感性是真陽性的比例,也就是真帶原者檢測陽性的比例。以統計檢定的型一錯誤(偽陽性)機率α和型二錯誤(偽陰性)β來表示:特異性=1-α;敏感性=1-β。
PPV(精密性)則是檢測陽性者真帶原的比例,它因此是敏感性的「反機率」,需要用貝氏定理來算,但用貝氏定理則必須納入先驗機率,這裡先驗率就是真帶原者佔檢測人口比例的初步估計,也就是盛行率π的估計值。我在附註文章中算得的結果是:
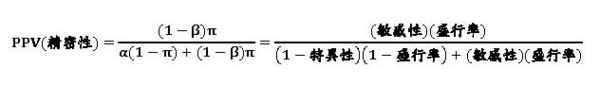
這個公式不論用在病毒核酸檢測(PCR)、快篩、或血清抗體檢測都是一樣的,但這三種檢測工具的特異性和敏感性則通常有所差別,因此即使盛行率一樣,它們的PPV也不會一樣。以台灣防疫中心和美國CDC所舉過的例子來看, 這三種工具的品質可列表比較如下:
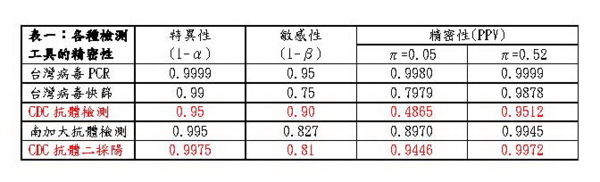
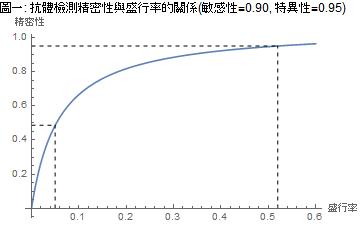
在盛行率π=0.05時,PPV=0.4865是什麼概念?它是說抗體檢測為陽性者,其中只有不到一半(48.65%)是真帶原者, 也就是偽陽性的比例超過一半!
那麼盛行率0.05又是什麼概念?以武漢為例,根據德國之聲中文網5月18日的報導,「武漢在全市範圍內開展了全員新冠病毒核酸篩查。財新網報導指出,初步評估武漢核酸檢測結果顯示,1000萬人中,至少有50萬人已經感染。」如果這個數字屬實,武漢的盛行率就是0.05,可見這樣的盛行率在全世界極高了。可是如果以美國CDC引為案例的檢測試劑在武漢全面實施抗體檢測,所得陽性結果中會有一半是偽陽性!
前述洛杉磯郡抗體檢測估計的盛行率為4.65%,也非常接近0.05了。如果也是用CDC引為案例的試劑做的抗體檢測,所得的35個確診數會有18個偽陽性。但是南加大研究團隊用的試劑特異性高達0.995,已經超過台灣CDC的快篩試劑特異性,敏感性也有0.827,所以它的PPV可以高達0.89,也就是35位確診者只有4位偽陽性。如果考慮盛行率的信心區間,PPV的信心區間為0.81-0.93,偽陽性在1-7位之間。
CDC在南加大的研究報告刊出之後發表【指導方針】也許不是偶然。當各地、各界、甚至各行各業開始相信新冠病毒感染致死率沒有原來想像中那麼高的時候,CDC及時發出指示,提醒大家要謹慎解讀抗體檢測的結果,以免貿然解封、復工可能帶來的災難。
1. 〈醫療檢測的準確度〉http://blog.udn.com/nilnimest/132657002
2. 〈陳時中說普篩會篩出很多偽陽性,那我們還能信賴防疫中心之前採檢的結果嗎?〉http://blog.udn.com/nilnimest/133411134
3. 〈貝氏定理在生活中很有用,可是它到底怎麼算?〉http://blog.udn.com/nilnimest/124668370



