化學反應熱, q,是路徑函數,取決於反應過程;但用狀態函數討論能量變化比較方便,特別是與反應是否發生無關

反應焓: ∆U=qᵥ if no work and constant V; ∆H=qₚ if no other work than pV work &costant p

∆H>0 吸熱反應會造成溫度下降(在絕熱條件下)

∆H<0 span="">放熱反應會造成溫度上升(在絕熱條件下)

標準焓變化量∆_rH^⦵ (p.s. ∆_rHª at 1 atm)

標準狀態: 純物質在1bar和特定溫度下的狀態, i.e. 1 bar=10⁵Pa, 特定溫度=25℃, ₮

s for solid, l for liquid, and g for gas. ex. H₂O₍ₗ₎ liquid water

C₍ₛ_{, graphite}₎+O₂₍_g₎→CO₂₍_g₎ ∆_rH^⦵(₮)=-393.5 kJmol⁻¹

化學反應式中均是未混合的反應物與產物;溶液中的離子反應除外,混不混合差別不大

生成反應熱, ∆_fH^⦵

元素的生成熱=0 at all temperatures.

Hesss law和反應焓

ex. 2NH₃₍ₗ₎+2NO₍_g₎→H₂O₂₍ₗ₎+4N₂₍_g₎ at ₮, ∆_rH^⦵=(-187.8+40)-(2264+290.25)=-896.3 kJmol⁻¹

一般的計算: aA+bB→cC+dD, 質量守恆 0=cC+dD-aA-bB or 0=∑_Jv_JJ, v_J:化學反應中平衡係數

∆_rH^⦵=(c∆_fH_C^⦵+d∆_fH_D^⦵)-(a∆_fH_A^⦵+b∆_fH_B^⦵) or ∆_rH^⦵=∑_Jv_J∆_fH_J^⦵, ∆_fH_J^⦵:J物質標準生成反應熱

Hesss law: 若一反應為二個反應式的代數和時,其反應熱為此二反應熱的代數和。在條件不變的情況下,化學反應的反應熱只與起始和終了狀態有關,與變化途徑無關

ex. 已知CH₂=CHCH₃₍_g₎+H₂₍_g₎→CH₃CH₂CH₃₍_g₎ ∆_rH^⦵=-124 kJmol⁻¹, CH₃CH₂CH₃₍_g₎+5O₂₍_g₎→3CO₂₍_g₎+4H₂O₍ₗ₎ ∆_rH^⦵=-2220 kJmol⁻¹, 求丙烯的燃燒熱?

丙烯的燃燒反應: C₃H₆₍_g₎+⁹/₂O₂₍_g₎→3CO₂₍_g₎+3H₂O₍ₗ₎ ∆_rH^⦵=?

C₃H₆₍_g₎+H₂₍_g₎→C₃H₈₍_g₎ ∆_rH^⦵=-124 kJmol⁻¹, +

C₃H₈₍_g₎+5O₂₍_g₎→3CO₂₍_g₎+4H₂O₍ₗ₎ ∆_rH^⦵=-2220 kJmol⁻¹, +

H₂O₍ₗ₎→H₂₍_g₎+½O₂₍_g₎ ∆_rH^⦵=+286 kJmol⁻¹ =

C₃H₆₍_g₎+⁹/₂O₂₍_g₎→3CO₂₍_g₎+3H₂O₍ₗ₎ ∆_rH^⦵=-2058 kJmol⁻¹

反應焓的溫度關係: 許多反應都不是在25℃ (₮)發生,如何估計在不同溫度的反應焓

因為Cₚ=(∂H/∂T)ₚ→H(T₂)=H(T₁)+(T₂-T₁)(∂H/∂T)ₚ=H(T₁)+(T₂-T₁)Cₚ if temp. change from T₁ toT₂ .

假設Cₚ與溫度無關,上面的式子可用在化學反應中每個物質,所以∆_rH^⦵可改寫成

∆_rH(T₂)=∆_rH(T₁)+(T₂-T₁)(Cₚ_,products-Cₚ_,reactants) 簡化為∆_rH(T₂)=∆_rH(T₁)+δT∆_rCₚ

更正規的方式(避免假設Cₚ與溫度無關), dH=CₚdT, ∫dH=H(T₂)-H(T₁)=∫_T₁^T₂Cₚ(T)dT, 同樣地應用於化學反應中每個物質J, ∆_rH(T₂)=∆_rH(T₁)+∫_T₁^T₂∆_rCₚ(T)dT Kirchhoffs law

i.e. ∆_rCₚ(T)=(cCₚ_,C+dCₚ_,D)-(aCₚ_,A+bCₚ_,B) in aA+bB→cC+dD, ∆_rCₚ=∑_Jv_JCₚ_,J

通常莫耳比熱的數學式: Cₚ_,J(T)=a_J+b_JT+c_J/T², a,b,c與溫度無關

∆_rH與∆_rU的關係: ∆_rH=∆_rU+(pV)_products-(pV)_reactants

若反應中只有固體和液體,反應前後體積大約相同, ∆_rH=∆_rU

反應中有氣體的話,假設都是理想氣體,pV項可以nRT取代: ∆_rH=∆_rU+∆v_gasRT

e.g. ∆v_gas=+1 in H₂O₍ₗ₎→H₂O₍_g₎, ∆v_gas: 反應中氣體莫耳數變化

ex. estimate ∆_rU^⦵(₮) fo r ammonia from ∆_fH^⦵(₮)

³/₂H₂₍_g₎+½N₂₍_g₎→NH₃₍_g₎, ∆v_gas=1-½-³/₂=-1 and at ₮, RT=2.48 kJmol⁻¹

∆_rU^⦵(₮)=∆_fH^⦵(₮)-∆v_gasRT=-46.1-(-1)2.48=-43.6 kJmol⁻¹

焓的種類

(i)燃燒焓, ∆_cH, e.g. (C,H,O,N)_compounds+O₂₍_g₎→CO₂₍_g₎+H₂O₍ₗ₎+N₂₍_g₎

ex. 葡萄糖燃燒, C₆H₁₂O₆₍ₛ₎+6O₂₍_g₎→6CO₂₍_g₎+6H₂O₍ₗ₎; ∆_cH^⦵=-2808 kJmol⁻¹ 此放熱反應是細胞活動的基礎(aerobic respiration有氧呼吸);

有些微生物的細胞反應效率較低,如厭氧發酵的糖酵解glycolysis,

C₆H₁₂O₆₍ₛ₎→^enzymes→2CH₃CH(OH)COOH₍ₛ₎; ∆_rH^⦵=-120 kJmol⁻¹,

然後乳酸燃燒,CH₃CH(OH)COOH₍ₛ₎+3O₂₍_g₎→3CO₂₍_g₎+3H₂O₍ₗ₎; ∆_cH^⦵=-1344 kJmol⁻¹

(ii) 生成焓, ∆_fH, 化合物生成焓是以元素被拆開成原子再組成化合物的過程來考慮,其中包含鍵結解離能∆H_D, e.g. ∆H(A-B), the reaction enthalpy for AB₍_g₎→A₍_g₎+B₍_g₎. 但須注意特定鍵結的解離能視分子其餘的結構而定, 如水的O-H鍵, ∆H^⦵(HO-H)=492 vs. ∆H^⦵(O-H)=428 kJmol⁻¹

鍵結解離能分為兩種: 1. bond dissociation energy, D(A-B),在零度發生解離的內能變化量 2. bond enthalpy, E(A-B), 一系列有關的化合物平均得到的A-B鍵解離能, 例如∆H^⦵(HO-H)和 ∆H^⦵(O-H)的均值463 kJmol⁻¹

(iii)原子化焓, ∆_aH,譬如水的∆_aH應該是HO-H 和O-H解離能的和,920 kJmol⁻¹; 對金屬而言∆_aH 也是昇華熱, M₍ₛ₎→M₍_g₎, e.g. ∆_aH(carbon)=716.68 kJmol⁻¹特別難測量

ex. 估計液態甲醇的生成焓, C₍ₛ₎+2H₂₍_g₎+½O₂₍_g₎→CH₃OH₍ₗ₎; 利用∆_aH和bond enthalpy的數據

1. ∆_aH^⦵(C)+2∆H(H-H)+½∆H(O=O)=717+2436+½ 497=1838 kJmol⁻¹

2. ∆Hₘ^⦵=-[3E(C-H)+E(C-O)+E(O-H)]=-(3413+360+463)=-2062 kJmol⁻¹

1+2, ∆_fHₘ=-224 kJmol⁻¹, 又凝結熱=-37.99 kJmol⁻¹,

液態甲醇的總生成焓,∆_fHₘ^⦵=-262 kJmol⁻¹(測量值-239)

ex. 2C₍ₛ₎+3H₂₍_g₎+½O₂₍_g₎→C₂H₅OH₍ₗ₎, 1. 2∆_aH^⦵(C)+3∆H(H-H)+½∆H(O=O)=2990.5, 2. -[5E(C-H)+E(C-C)+E(C-O)+E(O-H)]=-3236, 1+2=-245.5, and 凝結熱=-43.5 →∆_fHₑ^⦵=-289 kJmol⁻¹

(iv)昇華熱∆H_sub是相轉變焓的一個特例,蒸發熱∆H_vap,熔解熱∆H_melt也稱潛熱都屬之, ex. 水蒸發

H₂O₍ₗ₎→H₂O₍_g₎; ∆H^⦵_vap,m(₮)=+44.02, vs. +40.66 kJmol⁻¹ at 100℃.

at 100℃, ∆U_vap=∆H_vap-∆v_gasRT=40.66-3.1=37.56 kJmol⁻¹, 8% difference b/t ∆H_vap & ∆U_vap

(v)氫化焓: 乙烯與苯的氫化, CH₂=CH₂₍_g₎+H₂₍_g₎→CH₃CH₃₍_g₎ ∆_rH^⦵=-137 kJmol⁻¹,

C₆H₆₍ₗ₎+H₂₍_g₎→C₆H₁₂₍ₗ₎ ∆_rH^⦵=-205 kJmol⁻¹; 苯有3個碳雙鍵,反應熱應該是乙烯的3倍,為何只有-205?

(vi)溶液中離子的解離熱,∆H_soln,此焓假設無限稀薄溶液和離子間沒有作用的條件下;最常見的是水溶液aqueous solution, 例如:

HCl₍_g₎→HCl₍ₐ_q₎; ∆H^⦵_soln,m(₮)=-74.85 kJmol⁻¹,當鹽酸溶液比較濃時,生熱也會不同

根據Hess;s law,可得鹽酸溶液的生成熱: ½H₂₍_g₎+½Cl₂₍_g₎→HCl₍_g₎; ∆_rH^⦵=-92.31 kJmol⁻¹,前後兩式相加即得 ½H₂₍_g₎+½Cl₂₍_g₎→HCl₍ₐ_q₎; ∆_rH^⦵=-167.16 kJmol⁻¹

另一途徑可以將組成離子的解離熱相加; ½H₂₍_g₎→H⁺₍ₐ_q₎; ∆_rH^⦵=0 kJmol⁻¹, ½Cl₂₍_g₎→Cl⁻₍ₐ_q₎; ∆_rH^⦵=-167.2 kJmol⁻¹ e.g. define ½H₂₍_g₎→H⁺₍ₐ_q₎; ∆_rH^⦵=0 by convention.

→ ½H₂₍_g₎+½Cl₂₍_g₎→H⁺₍ₐ_q₎+Cl⁻₍ₐ_q₎; ∆_rH^⦵=-167.2 kJmol⁻¹, i.e. H⁺₍ₐ_q₎+Cl⁻₍ₐ_q₎=HCl₍ₐ_q₎

ex. a. 求Na₍ₛ₎+½Cl₂₍_g₎→NaCl₍ₐ_q₎的生成熱

Na₍ₛ₎→Na⁺₍ₐ_q₎; ∆_rH^⦵=-240.1 kJmol⁻¹, ½Cl₂₍_g₎→Cl⁻₍ₐ_q₎; ∆_rH^⦵=-167.2 kJmol⁻¹相加

Na₍ₛ₎+½Cl₂₍_g₎→NaCl₍ₐ_q₎; ∆_rH^⦵=-407.3 kJmol⁻¹

b. 求鹽的溶解熱, ∆H_solv,可以用Born-Haber cycle分步驟來解

1. 1. 鍵結解離能∆H_D, ½Cl₂₍_g₎→Cl₍_g₎; ½∆H_D=121 kJmol⁻¹

   2. 昇華熱∆H_sub, Na₍ₛ₎→Na₍_g₎; ∆H_sub=108.4 kJmol⁻¹

   3. 離子化∆H_I, Na₍_g₎→Na⁺₍_g₎+e⁻₍_g₎; ∆H_I=495.8+RT kJmol⁻¹

   4. 電子親和力E_A, Cl₍_g₎+e⁻₍_g₎→Cl⁻₍_g₎; E_A=-348.6-RTkJmol⁻¹

      

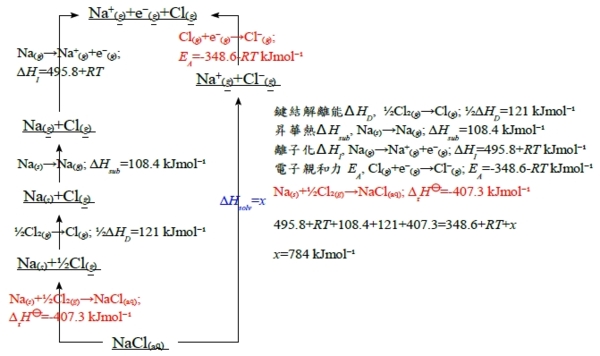
      ⸫ Na⁺₍_g₎+Cl⁻₍_g₎→NaCl₍ₐ_q₎; ∆_rH^⦵=-784 kJmol⁻¹

      c. 求鹽的晶格熱, ∆H^⦵_lattice, Na⁺₍_g₎+Cl⁻₍_g₎→NaCl₍ₛ₎

      

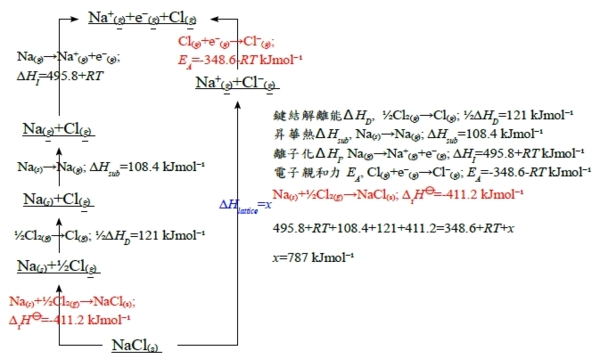
      ⸫ Na⁺₍_g₎+Cl⁻₍_g₎→NaCl₍ₛ₎; ∆H^⦵_lattice=-787 kJmol⁻¹