ch. 9 solution behavior

*gas mixing(ideal gas): 原子間距離遠,無相互作用力的問題; 100%混合無溶解度的問題

*condensed phase(liquid or solid): strong interaction between atoms, solubility issues in solid: 1. atom size difference in crystal(尺寸影響, Hume-Rothery rule). 2. 鍵結影響: 陰電性(從外抓電子的能力), 價數valence.

§Raoults law & Henrys law

1. pure liquid A: evaporation rate rₑ(A) and condensation rate r_ᶜ(A)=kp_ᴀ⁰

at equilibrium, rₑ(A)=r_ᶜ(A) → rₑ(A)=kp_ᴀ⁰

2. pure liquid B: evaporation rate rₑ(B) and condensation rate r_ᶜ(B)=kp_ᴃ⁰

at equilibrium, rₑ(B)=r_ᶜ(B) → rₑ(B)=kp_ᴃ⁰

3. B+(very small amount A): condensation rate of A r_ᶜ(A)=kp_ᴀ, condensation rate of B r_ᶜ(B)=kp_ᴃ

Assuming a. E_ᴀᴀ=E_ᴃᴃ=E_ᴀᴃ(bonding energy) i.e. Eᵢ_ʲ<0 b. surface composition=bulk composition, c.surface fraction of A=X_ᴀ

evaporation rate of A: rₑ(A)X_ᴀ; as equilibrium, rₑ(A)X_ᴀ=kp_ᴀ ⸪rₑ(A)=kp_ᴀ⁰ → X_ᴀp_ᴀ⁰=p_ᴀ ⸫ X_ᴃp_ᴃ⁰=p_ᴃ

X_ᴀ=p_ᴀ/p_ᴀ⁰, X_ᴃ=p_ᴃ/p_ᴃ⁰....Raoults law

4. if E_ᴀᴃ is more negative(|E_ᴀᴃ|>|E_ᴀᴀ| and |E_ᴀᴃ|>|E_ᴃᴃ|), evaporation rate of A, rₑ(A)<rₑ(A)

rₑ(A)X_ᴀ=kp_ᴀ → 同除以rₑ(A)=kp_ᴀ⁰ → rₑ(A)X_ᴀ/rₑ(A)=kp_ᴀ/kp_ᴀ⁰ → [rₑ(A)/rₑ(A)]X_ᴀ=p_ᴀ/p_ᴀ⁰

→ γ_ᴀX_ᴀ=p_ᴀ/p_ᴀ⁰ (γ_ᴀ<1) *γ_ᴀ is constant, independent of X_ᴀ(與成分無關)...Henrys law

p_ᴀ/p_ᴀ⁰=γ_ᴀX_ᴀ, p_ᴃ/p_ᴃ⁰=γ_ᴃX_ᴃ

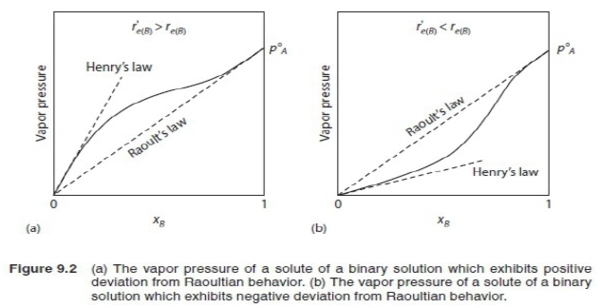
solution: (aᵢ/Xᵢ)≡γᵢ activity coeff.

Raoults law: aᵢ=Xᵢ (or γᵢ=1)

Henrys law: 1. aᵢ=γᵢXᵢ, γᵢ≠1 2. γᵢ independent of Xᵢ(有限範圍內有效,若超過臨界值,A原子周圍就不再都是B原子,與成分有關)

§Gibbs-Duhem eq.

Q=Q(T,P,nᵢ,n_ʲ,nₖ,....) in a solution composed of (nᵢ,n_ʲ,nₖ,....)

→dQ=(∂Q∕∂T)_{ᴘ,ₙᵢ,...}dT+(∂Q∕∂P)_{ᴛ,ₙᵢ,...}dP+(∂Q∕∂nᵢ)_{ᴛ,ᴘ,ₙʲ,...}dnᵢ+...

at fixed T,P dQ=Qᵢdnᵢ+Q_ʲdn_ʲ+Qₖdnₖ+...

Q=nᵢQᵢ+n_ʲQ_ʲ+nₖQₖ+... → dQ=Qᵢdnᵢ+Q_ʲdn_ʲ+Qₖdnₖ+...+(nᵢdQᵢ+n_ʲdQ_ʲ+nₖdQₖ+...)

∑nᵢdQᵢ=0, ∑XᵢdQᵢ=0...Gibbs-Duhem eq.

§Gibbs free energy of binary solution

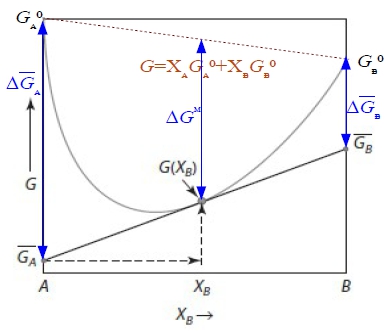
1. molar Gibbs free energy (G) ← solution(given)

partial Gibbs free energy G_ᴀ, G_ᴃ ← each component=?

⸪G=X_ᴀG_ᴀ+X_ᴃ G_ᴃ...(1) dG=G_ᴀdX_ᴀ+ G_ᴃdX_ᴃ+X_ᴀdG_ᴀ+X_ᴃ dG_ᴃ → dG=G_ᴀdX_ᴀ+ G_ᴃdX_ᴃ

binary X_ᴀ+X_ᴃ =1, dX_ᴀ=-dX_ᴃ ⸫dG=(G_ᴀ- G_ᴃ)dX_ᴀ , G_ᴀ- G_ᴃ=dG/dX_ᴀ ...(2)

(2)∙X_ᴃ+(1) → G+X_ᴃ(dG/dX_ᴀ)=(X_ᴀ+X_ᴃ ) G_ᴀ → G_ᴀ=G+(1-X_ᴀ)(dG/dX_ᴀ) or G_ᴃ=G+(1-X_ᴃ)(dG/dX_ᴃ)

Gᵢ=G+(1-Xᵢ)(dG/dXᵢ) 知其中之一即可求其餘自由能!

e.g. G=aX_ᴀX_ᴃ, G_ᴀ=? G=aX_ᴀ(1-X_ᴀ)=aX_ᴀ-aX_ᴀ², dG/dX_ᴀ=a-2aX_ᴀ ⸫ G_ᴀ=aX_ᴀX_ᴃ+X_ᴃ(a-2aX_ᴀ)= aX_ᴃ-aX_ᴀX_ᴃ=aX_ᴃ(1-X_ᴀ)=a(1-X_ᴀ)²

fixed T,P G=G(X_ᴀ,X_ᴃ )=G(X_ᴀ)=a+bX_ᴀ+cX_ᴀ²+...

2. ∆G^ᴹ, ∆G_ᴀ^ᴹ, ∆G_ᴃ^ᴹ i: component

1 mole i(pᵢ⁰) → mixed into solution(pᵢ), ∆Gᵢ=Gᵢ₍ₛₒₗ₎-Gᵢ₍ₚᵤᵣₑ₎=RTln(pᵢ/pᵢ⁰)=RTlnaᵢ

note: Gᵢ₍ₛₒₗ₎=Gᵢ, Gᵢ₍ₚᵤᵣₑ₎=Gᵢ⁰, ⸫∆Gᵢ=∆Gᵢ=Gᵢ-Gᵢ⁰=RTlnaᵢ

A: n_ᴀ and B: n_ᴃ mixing at (T,P), 混合前: G_ᵇᵉᶠ=n_ᴀG_ᴀ⁰+n_ᴃG_ᴃ⁰, 混合後: Gₐ_ᶠₜ=n_ᴀG_ᴀ+n_ᴃG_ᴃ

⸫∆G^ᴹ=Gₐ_ᶠₜ-G_ᵇᵉᶠ= n_ᴀ(G_ᴀ-G_ᴀ⁰)+n_ᴃ(G_ᴃ-G_ᴃ⁰)=n_ᴀ∆G_ᴀ+n_ᴃ∆G_ᴃ=n_ᴀRTlna_ᴀ+n_ᴃRTlna_ᴃ=RT(n_ᴀlna_ᴀ+n_ᴃlna_ᴃ)

→ ∆G^ᴹ=RT(X_ᴀlna_ᴀ+X_ᴃlna_ᴃ) 除以n_ᴀ+n_ᴃ成為molar Gibbs free energy.

or 直接寫 ∆G^ᴹ=X_ᴀRTlna_ᴀ+X_ᴃRTlna_ᴃ

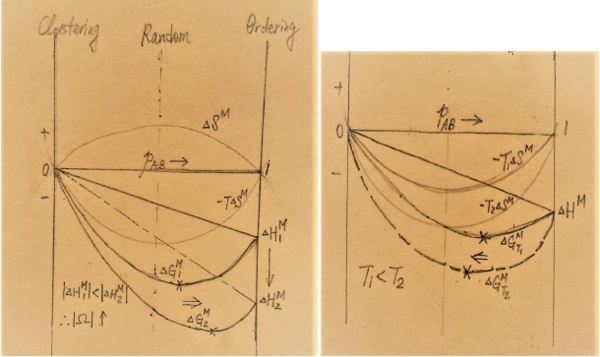
3. 圖解 Gᵢ(G_ᴀ,G_ᴃ), ∆Gᵢ(∆G_ᴀ,∆G_ᴃ) given: ∆G^ᴹ curve, ask ∆G_ᴀ=?, ∆G_ᴃ=?

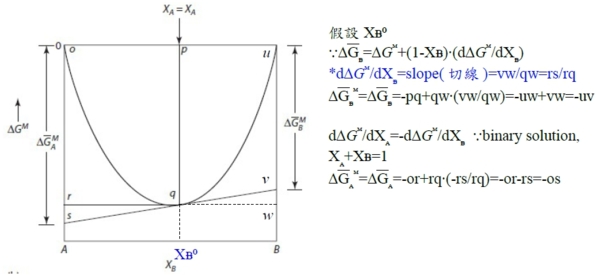
Given G₍ₛₒₗ₎, curve, ask G_ᴀ=?, G_ᴃ=?

§properties of ideal solution

ideal solution: E_ᴀᴀ=E_ᴃᴃ=E_ᴀᴃ(same bonding energy), aᵢ=Xᵢ (or γᵢ=1)

⸪∆Gᵢ=RTlnaᵢ ⸫∆Gᵢ=RTlnXᵢ ask ∆G^ᴹ=?, ∆H^ᴹ=? ∆S^ᴹ=?, ∆V^ᴹ=? 與ideal das 混合結果相同

∆G^ᴹ=RT∑XᵢlnXᵢ, ∆S^ᴹ=- R∑XᵢlnXᵢ, ∆H^ᴹ=0, ∆V^ᴹ=0

∆V^ᴹ=∑Xᵢ∆Vᵢ 由G求V→ dG=-SdT+VdP+∑ μᵢdnᵢ at fixed T, (∂G∕∂P)_ᵀ,ᶜₒₘₚ=V (ideal gas)

沿用至ideal solution, 混合後: Vᵢ=(∂Gᵢ∕∂P)_ᵀ,ᶜₒₘₚ, 混合前: Vᵢ⁰=(∂Gᵢ⁰∕∂P)_ᵀ

∆Vᵢ=Vᵢ-Vᵢ⁰=[∂(Gᵢ-Gᵢ⁰)∕∂P]_ᵀ,ᶜₒₘₚ=[∂(RTlnXᵢ)∕∂P]_ᵀ,ᶜₒₘₚ=0, Vᵢ=Vᵢ⁰ → ∆V^ᴹ=0

∆H^ᴹ=∑Xᵢ∆Hᵢ 由G求H→ Gibbs-Hlemholtz eq. 混合後: [∂(Gᵢ/T)∕∂T]_ᴾ,ᶜₒₘₚ=-Hᵢ/T², 混合前: [∂(Gᵢ⁰/T)∕∂T]_ᴾ,ᶜₒₘₚ=-Hᵢ⁰/T² → 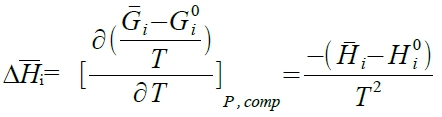, ⸪(Gᵢ-Gᵢ⁰)/T=RlnXᵢ, ⸫∆Hᵢ=0

∆S^ᴹ=? ∆G^ᴹ=∑Xᵢ∆Gᵢ=RT∑XᵢlnXᵢ, ∆G^ᴹ=∆H^ᴹ-T∆S^ᴹ, ∆S^ᴹ=-∆G^ᴹ/T=-R∑XᵢlnXᵢ

由G求S→ -(∂G∕∂T)_ᴾ,ᶜₒₘₚ=S → -(∂∆Gᵢ∕∂T)_ᴾ,ᶜₒₘₚ=∆Sᵢ=-RlnXᵢ, ∆S^ᴹ=∑Xᵢ∆Sᵢ=-R∑XᵢlnXᵢ

以binary solution為例,n_ᴀ mole A與n_ᴃ mole B 混合, 混合前entropy=S⁰, 混合後entropy=S

∆S^ᴹ=S-S⁰=klnΩ-klnΩ⁰=kln[(n_ᴀ+n_ᴃ)!/(n_ᴀ!n_ᴃ!)]-kln(n_ᴀ!/n_ᴀ!∙n_ᴃ!/n_ᴃ!)

i.e. 統計熱力 S≡klnΩ, stirling approx. LnN!≈NlnN-N

→ ∆S^ᴹ=k[(n_ᴀ+n_ᴃ)ln(n_ᴀ+n_ᴃ)-(n_ᴀ+n_ᴃ)-n_ᴀlnn_ᴀ+n_ᴀ-n_ᴃlnn_ᴃ +n_ᴃ] ″configuration entropy″

=-k{n_ᴀln[n_ᴀ/(n_ᴀ+n_ᴃ)]+n_ᴃln[n_ᴃ /(n_ᴀ+n_ᴃ)]}=-k[n_ᴀlnX_ᴀ+n_ᴃlnX_ᴃ]=-k(n_ᴀ+n_ᴃ)[X_ᴀlnX_ᴀ+X_ᴃlnX_ᴃ]

=-k∙N_ᴀ∙n(X_ᴀlnX_ᴀ+X_ᴃlnX_ᴃ)=-R∙n(X_ᴀlnX_ᴀ+X_ᴃlnX_ᴃ) → ∆S^ᴹ=-R(X_ᴀlnX_ᴀ+X_ᴃlnX_ᴃ), ⸫∆S^ᴹ=-R∑XᵢlnXᵢ

e.g. Vacancy or impurity, 從自由能看平衡濃度, ∆G^ᴹ=∆H^ᴹ-T∆S^ᴹ, 焓視為形成空位所必需的能量,另一方面空位加入晶格中(如二元溶液混合)造成亂度增加,最後∆G^ᴹ=0達到平衡

equilibrium N_V =Ne⁻^Qᵛ^/ᴿᵀ, k=-1.38∙10⁻²³ J/K Boltzmanns constant

i.e. N: total # of atomic site, Q_v: energy required for the formation of a vacancy.

§non-ideal solution, γᵢ≡aᵢ/Xᵢ, γᵢ≠1(γᵢ>1 or γᵢ<1) → γᵢ=f(Xᵢ,T)

⸪∆Gᵢ=RTlnaᵢ=RTlnXᵢ+RTlnγᵢ → ∆Hᵢ≠0

∆Gᵢ=RTlnaᵢ → 求∆Hᵢ [∂(∆Gᵢ/T)∕∂T]_ᴾ,ᶜₒₘₚ=-∆Hᵢ/T² → [∂(Rlnγᵢ)∕∂T]_ᴾ,ᶜₒₘₚ=-∆Hᵢ/T² → [∂(Rlnγᵢ)∕∂(1/T)]_ᴾ,ᶜₒₘₚ=-∆Hᵢ

notes: case #1. γᵢ≠f(T), independent of T. ∆Hᵢ=0

case #2. in general, γᵢ=f(T)

e.g. If γ_ᴀ>1 in binary solution, γ_ᴀ≡[rₑ(A)/rₑ(A)]表示|E_ᴀᴃ|<|E_ᴀᴀ|, A-B bonding比較弱,solute A容易蒸發; 另外任何溶液溫度升高,亂度加大,使 γᵢ→1, ⸫dγᵢ/dT<0, dlnγᵢ/dT<0.

Case #3. If γᵢ>1, 溫度升高使 γᵢ→1, ⸫dγᵢ/dT<0, dlnγᵢ/dT<0 → ∆Hᵢ>0 endothermic reaction, |E_ᴀᴃ|<|E_ᴀᴀ|, clustering

case #4. If γᵢ<1, 溫度升高使 γᵢ→1, ⸫dγᵢ/dT>0, dlnγᵢ/dT>0 → ∆Hᵢ<0 exothermic reaction, |E_ᴀᴃ|>|E_ᴀᴀ|, ordering to form compound.

§application of Gibbs-Duhem eq.

1. given a_ᴃ(X_ᴃ) → calculate a_ᴀ(X_ᴀ) 2. if solute follows Henrys law, solvent would follows Raoults law. The same result in the opposite way. 3. given a_ᴀ(X_ᴀ) → calculate ∆G^ᴹ=?

∑XᵢdQᵢ=0...Gibbs-Duhem eq. ⸫∑XᵢdGᵢ=0 → RT∑Xᵢdlnaᵢ=0

binary solution, X_ᴀdlna_ᴀ+X_ᴃdlna_ᴃ=0 → dlna_ᴀ=-(X_ᴃ/X_ᴀ)dlna_ᴃ,

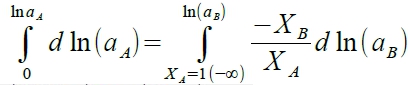
X_ᴀdlna_ᴀ+X_ᴃdlna_ᴃ=0 → X_ᴀdlnX_ᴀ+X_ᴀdlnγ_ᴀ+X_ᴃdlnX_ᴃ+X_ᴃdlnγ_ᴃ=0

⸪ X_ᴀdlnX_ᴀ+X_ᴃdlnX_ᴃ=X_ᴀ(dX_ᴀ/X_ᴀ)+X_ᴃ(dX_ᴃ/X_ᴃ)=dX_ᴀ+dX_ᴃ=0,

⸫X_ᴀdlnγ_ᴀ+X_ᴃdlnγ_ᴃ=0 → dlnγ_ᴀ=-(X_ᴃ/X_ᴀ)dlnγ_ᴃ→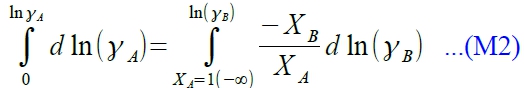

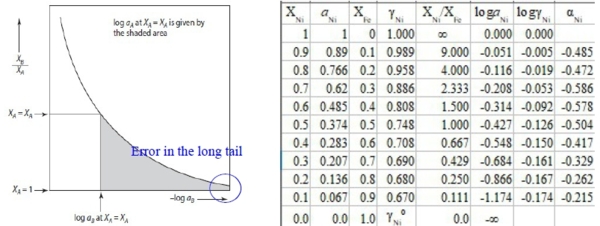
when X_ᴃ→1 or X_ᴀ→0 ⸫γ_ᴃ→1, lnγ_ᴃ=0; 1-X_ᴃ→0, α_ᴃ=lnγ_ᴃ/(1-X_ᴃ)²→finite value

lnγ_ᴀ= -X_ᴀX_ᴃ α_ᴃ-∫_Xᴀ=1α_ᴃdX_ᴀ...(M3)

dlnγ_ᴀ=-(X_ᴃ/X_ᴀ)∙(2α_ᴃ X_ᴀdX_ᴀ+X_ᴀ²dα_ᴃ)=-2α_ᴃ X_ᴃ dX_ᴀ-X_ᴀ X_ᴃ dα_ᴃ

d(α_ᴃX_ᴀ X_ᴃ)=X_ᴀ X_ᴃ dα_ᴃ+α_ᴃ X_ᴃdX_ᴀ+α_ᴃ X_ᴀdX_ᴃ 移項代入上式

dlnγ_ᴀ=-2α_ᴃ X_ᴃ dX_ᴀ-d(α_ᴃX_ᴀ X_ᴃ)+α_ᴃ X_ᴃdX_ᴀ+α_ᴃ X_ᴀ dX_ᴃ=-d(α_ᴃX_ᴀ X_ᴃ)-α_ᴃ (X_ᴃdX_ᴀ-X_ᴀdX_ᴃ) ⸪ dX_ᴀ=-dX_ᴃ

dlnγ_ᴀ=-d(α_ᴃX_ᴀ X_ᴃ)-α_ᴃdX_ᴀ → 積分即得

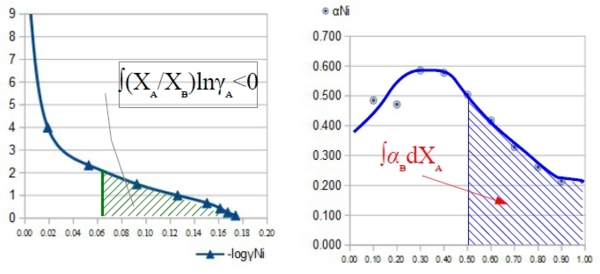
3. 已知a_ᴃ, ∆G_ᴃ=RTlna_ᴃ, 求∆G^ᴹ=?

⸪ ∆G_ᴃ=∆G^ᴹ+(1-X_ᴃ)∙(d∆G^ᴹ/dX_ᴃ ) → ∆G_ᴃdX_ᴃ=∆G^ᴹdX_ᴃ +(1-X_ᴃ)d∆G^ᴹ → ∆G_ᴃdX_ᴃ=-∆G^ᴹdX_ᴀ+X_ᴀd∆G^ᴹ

除以X_ᴀ² → ∆G_ᴃdX_ᴃ/X_ᴀ²=(-∆G^ᴹdX_ᴀ+X_ᴀd∆G^ᴹ)/X_ᴀ²=d(∆G^ᴹ/X_ᴀ) →積分

→

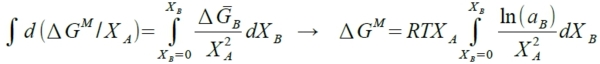
Ex. Fe-Ni, a_ᴺᵢ; Fe-Cu, a_ᴄᵤ

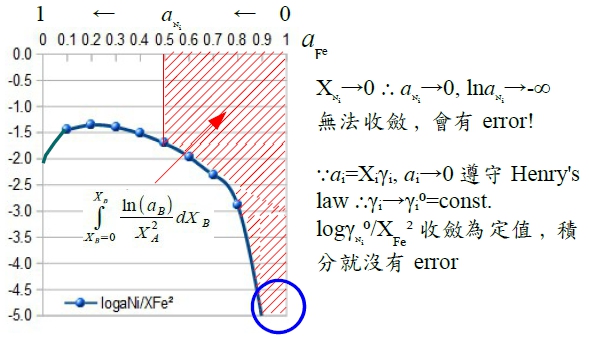
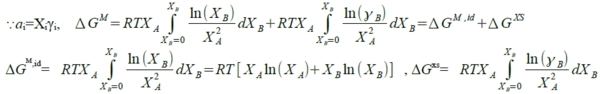
2. solute B follows Henrys law, solvent A will follow Raoults law.

γ_ᴃ=γ_ᴃ⁰=constant, pf: ⸪a_ᴃ=X_ᴃγ_ᴃ⁰, ⸫lna_ᴃ =lnX_ᴃ+lnγ_ᴃ⁰ → dlna_ᴃ =dlnX_ᴃ ; G-D eq. dlna_ᴀ=-(X_ᴃ/X_ᴀ)dlna_ᴃ

→ dlna_ᴀ=-(X_ᴃ/X_ᴀ)dlnX_ᴃ=-(X_ᴃ/X_ᴀ)∙(dX_ᴃ /X_ᴃ)=-dX_ᴃ /X_ᴀ=dX_ᴀ /X_ᴀ=dlnX_ᴀ → 積分 ∫dlna_ᴀ=∫dlnX_ᴀ

lna_ᴀ=lnX_ᴀ , a_ᴀ=X_ᴀ 反向也可證明

§Regular solution

*ideal: aᵢ=Xᵢ or γᵢ=1, ∆Hᵢ=0, ∆Sᵢ=-RlnXᵢ, ∆Gᵢ=RTlnXᵢ

*non-ideal: γᵢ≠1 and γᵢ≠const. γᵢ=f(Xᵢ,T) → ∆Hᵢ=-T²[∂(Rlnγᵢ)∕∂T]_ᴾ,ᶜₒₘₚ≠0=f(Xᵢ,T) 太複雜了!

找一個simplest function of ∆Hᵢ → Regular solution!

Define „regular solution” in mathematic form: 1. ∆Sᵢ=∆Sᵢ^id =-RlnXᵢ, 2. ∆Hᵢ=f(Xᵢ) only! Indep. of T.

∆H^ᴹ=∑Xᵢ∆Hᵢ=f"(Xᵢ), 特性: 當X_ᴀ→0, X_ᴃ→1 or X_ᴀ→1, X_ᴃ→0時, ∆H^ᴹ→0

⸫∆H^ᴹ=X_ᴀX_ᴃ(α+bX_ᴀ +cX_ᴀ²+...), simplest form: ∆H^ᴹ=X_ᴀX_ᴃα

求∆H_ᴀ=?, ∆H_ᴃ=? ∆Hᵢ=∆H^ᴹ+(1-Xᵢ)(d∆H^ᴹ/dXᵢ), ∆H^ᴹ=αX_ᴀ(1-X_ᴀ)=αX_ᴀ-αX_ᴀ²

⸫∆H_ᴀ=X_ᴀX_ᴃα+(1-X_ᴀ)(α-2αX_ᴀ)=X_ᴀX_ᴃα+X_ᴃ(α-2αX_ᴀ)=αX_ᴃ-αX_ᴀ X_ᴃ=αX_ᴃ(1-X_ᴀ)=αX_ᴃ²

∆H_ᴀ=α(1-X_ᴀ)², ∆H_ᴃ=α(1-X_ᴃ)², ∆G_ᴀ=∆H_ᴀ-T∆S_ᴀ=RTlna_ᴀ=RTlnX_ᴀ+RTlnγ_ᴀ=RTlnγ_ᴀ-T(-RlnX_ᴀ)

⸫∆H_ᴀ=RTlnγ_ᴀ 前面define: α function, αᵢ≡lnγᵢ/(1-Xᵢ)² → α_ᴀ=lnγ_ᴀ/(1-X_ᴀ)²

α_ᴀ=lnγ_ᴀ/(1-X_ᴀ)²=1/(1-X_ᴀ)²∙[α(1-X_ᴀ)²/RT]=α/RT ⸪∆H_ᴀ=α(1-X_ᴀ)²=RTlnγ_ᴀ 同時α_ᴃ= α/RT=α_ᴀ=α

→ α=αRT 物理意義?

§Excess quantity, „XS” ∆Sᵢ^ₓₛ, ∆Hᵢ^ₓₛ, ∆Gᵢ^ₓₛ

∆Gᵢ=RTlnaᵢ=RTlnXᵢ+RTlnγᵢ=∆Gᵢ^id+∆Gᵢ^ₓₛ,

∆G^ᴹ=∑Xᵢ∆Gᵢ=∆H^ᴹ-T∆S^ᴹ ⸫∆G^ₓₛ=∆G^ᴹ-∆G^ᴹ,id=(∆H^ᴹ-∆H^ᴹ,id)-T(∆S^ᴹ-∆S^ᴹ,id) ⸪∆H^ᴹ,id=0, ∆S^ᴹ=∆S^ᴹ,id

→∆G^ₓₛ=∆H^ᴹ, ∆G^ₓₛ=RT(X_ᴀlnγ_ᴀ+X_ᴃlnγ_ᴃ)=∆H^ᴹ, ∆G^ₓₛ= RT∑ Xᵢlnγᵢ

Regular solution: α_ᴃ=α_ᴀ=α, lnγ_ᴀ=α(1-X_ᴀ)², lnγ_ᴃ=α(1-X_ᴃ)²代入上式∆G^ₓₛ

⸫∆G^ₓₛ=∆H^ᴹ=RTαX_ᴀX_ᴃ=αX_ᴀX_ᴃ indep. of T.

∆S^ₓₛ=0, ∆S^ₓₛ=-(∂∆G^ₓₛ∕∂T)_ᴾ,ᶜₒₘₚ=0

*At a fixed composition, ∆G_ᴀ^ₓₛ=RTlnγ_ᴀ → RT₁lnγ_ᴀ₁=RT₂lnγ_ᴀ₂ → lnγ_ᴀ₁/lnγ_ᴀ₂=T₂/T₁

Summary for simplest regular solution:

∆Sᵢ^ₓₛ=0, ∆Hᵢ^ₓₛ=RTlnγᵢ, ∆Gᵢ^ₓₛ=RTlnγᵢ

1. ∆G^ₓₛ=∆H^ᴹ=RTαX_ᴀX_ᴃ=αX_ᴀX_ᴃ 2. ∆Gᵢ^ₓₛ=∆Hᵢ^ₓₛ=RTlnγᵢ 3. ∆Sᵢ^ₓₛ=0, ∆S^ₓₛ=0, ∆Sᵢ=∆Sᵢ^id =-RlnXᵢ 4. α_ᴃ=α_ᴀ=α=α/RT

實例判斷:

1. if ∆H^ᴹ=bX_ᴀX_ᴃ, ∆G^ₓₛ=bX_ᴀX_ᴃ, b≠b→ ∆G^ₓₛ≠∆H^ᴹ non-regular!

e.g. Au-Cu at 1550K, ∆G^ₓₛ=-24060X_AuX_Cu and ∆H^ᴹ non-symmetric → non-regular!

Au-Ag at 1350K, ∆H^ᴹ=-20590X_AuX_Ag and ∆G^ₓₛ non-symmetric → non-regular!

2. T=800K,

∆G^ₓₛ=∆H^ᴹ=X_ᴀX_ᴃ(α+bX_ᴀ)≠f(T), e.g. Au-Ag at 1350K, ∆G^ₓₛ=∆H^ᴹ=X_ᴀX_ᴃ(α+bX_ᴀ ), α=-11320J, b=1940J

*non-regular: ∆G^ₓₛ=(a+bX_ᴀ)X_ᴀX_ᴃ∙(1-T/τ)=f(T), ∆S^ₓₛ=-(∂∆G^ₓₛ∕∂T)_ᴾ,ᶜₒₘₚ=1/τ(a+bX_ᴀ)X_ᴀX_ᴃ≠0

∆H^ᴹ=∆H^ₓₛ=∆G^ₓₛ+T∆S^ₓₛ=(a+bX_ᴀ)X_ᴀX_ᴃ→ ∆G^ₓₛ≠∆H^ᴹ non-regular!

§Quasi-chemical model of solution, 以統計方法解釋α的物理意義

e.g. Binary solution, A+B, N_ᴀ atoms and N_ᴃ atoms(N_ᴀ+N_ᴃ=N₀=6.02∙10²³)

考慮 ∆H^ᴹ=∆U^ᴹ+P∆V^ᴹ, assume ∆V^ᴹ=0, ⸪V_ᴀ⁰=V_ᴀ=V_ᴃ= V_ᴃ⁰; ∆H^ᴹ=∆U^ᴹ=∆E^ᴹ (鍵結能變化)

鍵結能, E=ꝑ_ᴀᴀE_ᴀᴀ+ꝑ_ᴃᴃE_ᴃᴃ+ꝑ_ᴀᴃE_ᴀᴃ, i.e. Eᵢ_ʲ: bonding energy of i-j, ꝑᵢ_ʲ: # of i-j bonds

假設A原子的配位數為Z_ᴀ, N_ᴀ原子的鍵結數可表示成: N_ᴀ∙Z_ᴀ=2ꝑ_ᴀᴀ+ꝑ_ᴀᴃ → ꝑ_ᴀᴀ=½(N_ᴀ∙Z_ᴀ-ꝑ_ᴀᴃ), 同理

B原子的配位數設為Z_ᴃ, N_ᴃ原子的鍵結數可表示成: N_ᴃ∙Z_ᴃ=2ꝑ_ᴃᴃ+ꝑ_ᴃᴀ → ꝑ_ᴃᴃ=½(N_ᴃ∙Z_ᴃ-ꝑ_ᴃᴀ)

代入鍵結能式中, E= ½N_ᴀ∙Z_ᴀE_ᴀᴀ+½N_ᴃ∙Z_ᴃE_ᴃᴃ+ꝑ_ᴀᴃ[E_ᴀᴃ- ½(E_ᴀᴀ+E_ᴃᴃ)]

Pure A: N_ᴀ∙Z_ᴀ=2ꝑ_ᴀᴀ, E_ᴀ⁰=ꝑ_ᴀᴀE_ᴀᴀ= ½N_ᴀ∙Z_ᴀE_ᴀᴀ; Pure B: N_ᴃ∙Z_ᴃ=2ꝑ_ᴃᴃ, E_ᴃ⁰=ꝑ_ᴃᴃE_ᴃᴃ=½N_ᴃ∙Z_ᴃE_ᴃᴃ

∆E^ᴹ=E-(E_ᴀ⁰+E_ᴃ⁰)=ꝑ_ᴀᴃ[E_ᴀᴃ- ½(E_ᴀᴀ+E_ᴃᴃ)] Assume Z_ᴀ=Z_ᴃ=Z, ꝑ_ᴀᴃ=?

在計算ꝑ_ᴀᴃ之前, ⸪regular solution的定義: ∆Sᵢ=∆Sᵢ^id =-RlnXᵢ, 表示溶液處於complete random的條件下, 原子間鍵結沒有偏好。換言之,某一固定溫度的熱能足以彌補原子間鍵結能的差異,還是處於complete random. 例如: Arrehnius eq. D=D₀e⁻^q/ᵏᵀ= D₀e⁻^Q/ᴿᵀ 視為粒子的活化能q與kT做比較或Q與平均熱能RT比較,得到的平衡量。因此|∆H^ᴹ|≤RT視為溶液處於complete random

∆H^ᴹ≈∆E^ᴹ=ꝑ_ᴀᴃ[E_ᴀᴃ- ½(E_ᴀᴀ+E_ᴃᴃ)] 考慮A-B鍵數, 相鄰位置A-B配對的機率: ℓ_ᴀᴃ=2X_ᴀX_ᴃ

total # of bond=½N₀∙Z, ⸫ ꝑ_ᴀᴃ=½N₀∙Zℓ_ᴀᴃ =N₀∙ZX_ᴀX_ᴃ

∆H^ᴹ=X_ᴀX_ᴃ∙N₀Z[E_ᴀᴃ- ½(E_ᴀᴀ+E_ᴃᴃ)] compare with regular ∆H^ᴹ=X_ᴀX_ᴃα

let Ω≡N₀Z[E_ᴀᴃ- ½(E_ᴀᴀ+E_ᴃᴃ)] 鍵結能差異 → Ω=α=RTα

∆H^ᴹ=ΩX_ᴀX_ᴃ=∆G^ₓₛ, ∆Hᵢ=? ∆H_ᴀ=Ω(1-X_ᴀ)², ∆H_ᴃ=Ω(1-X_ᴃ)², ∆S_ᴀ=-RlnX_ᴀ, ∆S_ᴃ=-RlnX_ᴃ

∆G_ᴀ=∆H_ᴀ-T∆S_ᴀ=Ω(1-X_ᴀ)²-T(-RlnX_ᴀ) vs. ∆G_ᴀ=RTlna_ᴀ=RTlnX_ᴀ+RTlnγ_ᴀ

⸫ RTlnγ_ᴀ=Ω(1-X_ᴀ)² → lnγᵢ=(Ω/RT)∙(1-Xᵢ)²

notes: 1. if Ω=0, E_ᴀᴃ=½(E_ᴀᴀ+E_ᴃᴃ) → γᵢ=1 ideal solution

2. if Ω<0, ∆H^ᴹ<0 exothermic, ⸪Eᵢ_ʲ<0 ⸫ |E_ᴀᴃ|>½|E_ᴀᴀ+E_ᴃᴃ| → γᵢ<1 negative deviation

3. if Ω>0, ∆H^ᴹ>0 endothermic, ⸪Eᵢ_ʲ<0 ⸫ |E_ᴀᴃ|<½|E_ᴀᴀ+E_ᴃᴃ| → γᵢ>1 positive deviation

4. Henrys law: aᵢ=γᵢ⁰Xᵢ, as Xᵢ→0 γᵢ⁰=constant=e^Ω/ᴿᵀ

5. regular solution重要條件需要complete random, when |E_ᴀᴃ|>>½|E_ᴀᴀ+E_ᴃᴃ| → |Ω|鍵結能差異很大,會破壞complete random, 不適合用regular solution 模擬

6. equilibrium „configuration” of solution at fixed T, P

Equlibrium means ∆Gₘᵢₙ, ∆G=∆H-T∆S

regular: ∆H^ᴹ=ꝑ_ᴀᴃ[E_ᴀᴃ- ½(E_ᴀᴀ+E_ᴃᴃ)], ꝑ_ᴀᴃ=(½N₀∙Z)∙ℓ_ᴀᴃ ℓ_ᴀᴃ: probability of A-B bond ⸫∆H^ᴹ=½ℓ_ᴀᴃ Ω

Ex-1. Cu-Au solid solution at 873K, regular: ∆G^ₓₛ,=-28280X_AuX_Cu J/mole.

Given: pure lnp_Cu⁰=-40920/T-0.86lnT+21.67 pure lnp_Au⁰=-45650/T-0.306lnT+10.81

ask p_Au=? p_Cu=? at X_cu=0.6

a_Cu=f_Cu/f_Cu⁰=p_Cu/p_Cu⁰, a_Au=p_Au/p_Au⁰; aᵢ=γᵢXᵢ=pᵢ/pᵢ⁰ and lnγᵢ=(Ω/RT)∙(1-Xᵢ)², 先求γ_Au, γ_Cu即可得 a_Cu, a_Au

αᵢ≡lnγᵢ/(1-Xᵢ)²=Ω/RT, α_ᴃ=α_ᴀ=α=α/RT

Ex-2. Ga-Cd liquid solution at 700K, regular: X_Ga=0.5, a_Ga=0.79. Ask E_ga-Cd=?

Given: ΔHₑᵥₐₚ_,Ga=270000J, ΔHₑᵥₐₚ_,Cd=100000J, Z_Ga=11, Z_Cd=8

Ω≡N₀Z[E_ᴀᴃ- ½(E_ᴀᴀ+E_ᴃᴃ)] let A=Ga, B=Cd; ΔHₑᵥₐₚ_,i=½N₀∙ZEᵢᵢ → 求E_ᴀᴀ, E_ᴃᴃ

E_Ga-Ga=-8.15∙10⁻²⁰J, E_Cd-Cd=-4.15∙10⁻²⁰J

lnγᵢ=(Ω/RT)∙(1-Xᵢ)² 從γᵢ求出Ω, 代入Ω定義式中求E_Ga-Cd

γ_Ga=a_Ga/X_Ga=1.39 → lnγ_Ga=(Ω/RT)∙(1-X_Ga)² ⸫Ω=10745J Assume Z=½(Z_Cd+Z_Ga)=9.5

E_ga-Cd=-5.96∙10⁻²⁰J