Chap. 3 Electrolytic conductance 電解溶液的導電性

electrical conductivity, cond.= 1/resist. Resistivity, ρ=RA/L i.e. A: cross-sction area, L: length

conductivity, κ=1/ρ=L/RA....(1)

Molar conductivity in electrolyte solution: Λ=κ/C C:concentration in mol m⁻³(mM)

concentration dependence: Λ=Λ°-s√C Λ°:infinite dilution case, Λ°=ν₊Λ₊°+ν₋Λ₋°

transference number: t₊, t₋ and t₊+t₋=1

t₊=ν₊Λ₊/Λ, t₋=ν₋Λ₋/Λ where ν₊Λ₊+ν₋Λ₋=Λ

如何去量t₊, t₋ ? cond. 與t₊, t₋有關(hittorf cell)

mobility, uᵢ=|vᵢ|/|E| vᵢ: velocity, E: 電場

electric current i=ΔΦ/R, E=-ΔΦ/L and R=L/κA ⸫i=-κAE

(i/A)ᵢ=CᵢzᵢFvᵢ= -κᵢE

因此 vᵢ=-κᵢE/CᵢzᵢF, uᵢ=κᵢ/Cᵢ|zᵢ|F=Λᵢ/|zᵢ|F ⸫ Λᵢ=uᵢ|zᵢ|F.....(2)

Frictional coefficient, fᵢ

viscous drag force Fᵢ=fᵢvᵢ, and under steady-state condition fᵢvᵢ=zᵢeE

uᵢ=|vᵢ|/|E|=|zᵢ|e/fᵢ and Λᵢ=zᵢ²Fe/fᵢ

Stokes radius, rᵢ, effective size 與hydrodynamicsize有關

viscosity, η fᵢ=6πηrᵢ

uᵢ=|zᵢ|e/fᵢ=|zᵢ|e/6πηrᵢ → rᵢ=|zᵢ|e/6πηuᵢ 速度與rᵢ 成反比

ex. 用AC frequency適當調整, 可以使ion不受rᵢ影響conductivity, 測出真正的Λ°

theoretical calculation:

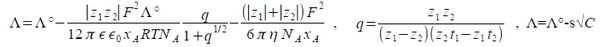
i.e. z₁, z₂: positive and negative ion charges, x_ᴀ: ion atnosphere thickness

diffusion

concentration gradient

1. Ficks 1^st law, J=-D(∂c/∂x)

ex. 電鍍時diffusion會影響電鍍層表面粗糙度

2. 2^nd law

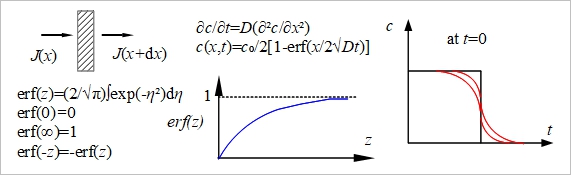
a. Carburizing, c=cₛ[1-erf(x/2√Dt)]

b. De-carburizing, c=(c₀-cₛ)erf(x/2√Dt)

motion of ion

μᵢ: chemical potential, ηᵢ=μᵢ+zeϕ

vᵢ=-1/fᵢ(∂ηᵢ/∂x), dηᵢ=dμᵢº+RTdlnaᵢ+zᵢedϕ → vᵢ=-1/fᵢ(RTdlnaᵢ/dx+zᵢedϕ/dx)

a. activity gradient=0, vᵢ= -|zᵢ|eE/fᵢ → |vᵢ|/E=|zᵢ|e/fᵢ=uᵢ

b. dϕ/dx=0, E=0, vᵢ= -1/fᵢ(RTdlnaᵢ/dx)≈-1/fᵢ(RTdlncᵢ/dx)=-RT/fᵢ(1/cᵢ)(dcᵢ/dx)

Jᵢ=vᵢcᵢ= -RT/fᵢ(dcᵢ/dx) ⸫Dᵢ= RT/fᵢ

Gas: D≈ 10⁻¹ cm²/sec, Liq.: D≈ 10⁻⁶ cm²/sec, Solid: D≈ 10⁻⁸ cm²/sec(快熔化時) or D≈ 10⁻¹⁶ cm²/sec

fᵢ=RT/Dᵢ and fᵢ=|zᵢ|e/uᵢ → RT/Dᵢ=|zᵢ|e/uᵢ Einstein relationship

uᵢ=|zᵢ|eDᵢ/RT and uᵢ=Λᵢ/|zᵢ|e ⸫Dᵢ= ΛᵢRT/|zᵢ|²e²

ex. Na⁺, Mg⁺⁺, Al³⁺ Λ° depend on charge on ion, D° depend on concentration of ion.

Junction potential, Δϕ

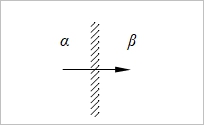
δQ=ΣFzᵢδnᵢ, tᵢ=Fzᵢδnᵢ/FΣzᵢδnᵢ=Fzᵢδnᵢ/δQ, δnᵢ=(tᵢ/zᵢ)(δQ/F)

ΔG=Σdηᵢδnᵢ, ηᵢ=μᵢº+RTlnaᵢ+zᵢFϕ → dηᵢ=RTdlnaᵢ+zᵢFdϕ

→ ΔG=Σ(RTdlnaᵢ+zᵢFdϕ)δnᵢ=Σ(RTtᵢ/zᵢF)dlnaᵢδQ+ tᵢδQdϕ=[(RT/F)Σ(tᵢ/zᵢ)dlnaᵢ+Σtᵢdϕ]δQ

When equilibrium, ΔG=0 → dϕ=-(RT/F)Σ(tᵢ/zᵢ)dlnaᵢ ⸪Σtᵢ=1

積分 Δϕ=ϕ_β-ϕ_α=

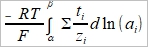 , for 1:1 solution, z₁=1, z₂=-1

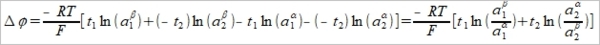
也可寫成 

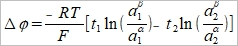
if a₁^α=a₂^α=a^α, a₁ᵝ=a₂ᵝ=aᵝ, 

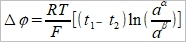
Henderson assumption cᵢ(x)=cᵢᵝx+cᵢ^α(1-x)

dlnaᵢ/dx=dlncᵢ/dx=(1/cᵢ)(dcᵢ/dx) → dcᵢ/dx=cᵢᵝ- cᵢ^α

dlnaᵢ=(dlnaᵢ/dx)dx=[(cᵢᵝ- cᵢ^α)/cᵢ]dx....(a) and tᵢ=zᵢcᵢ(x)uᵢ/Σ|z_j|c_j(x)u_j.....(b)

(a), (b)代入junction potential

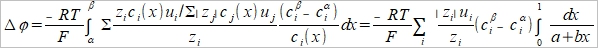
where a=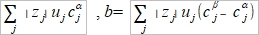

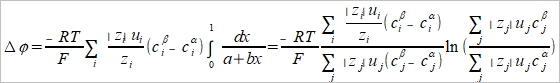
Donnan membrane

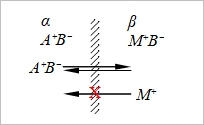
μᵢº^α+RTlnaᵢ^α+zᵢFϕ_α=μᵢºᵝ+RTlnaᵢᵝ+zᵢFϕᵦ

for i=1 RTlna₁^α=RTlna₁ᵝ+z₁FΔϕ.....(1) if z₁=-z₂

for i=2 RTlna₂^α=RTlna₂ᵝ+z₂FΔϕ.....(2)

(1)+(2), RTlna₁^αa₂^α=RTlna₁ᵝa₂ᵝ → a₁^αa₂^α=a₁ᵝa₂ᵝ

Δϕ=(RT/F)ln(a₁^α/a₁ᵝ)=(RT/F)ln(a₂ᵝ/a₂^α)

if γᵢ^α=γᵢᵝ → c₁^αc₂^α=c₁ᵝc₂ᵝ

考慮電中性: in α, c₁^α-c₂^α=0; in β, zero-charge condition → c₁ᵝ-c₂ᵝ+z_ᴍc_ᴍ=0