
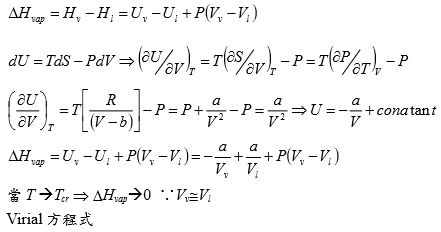

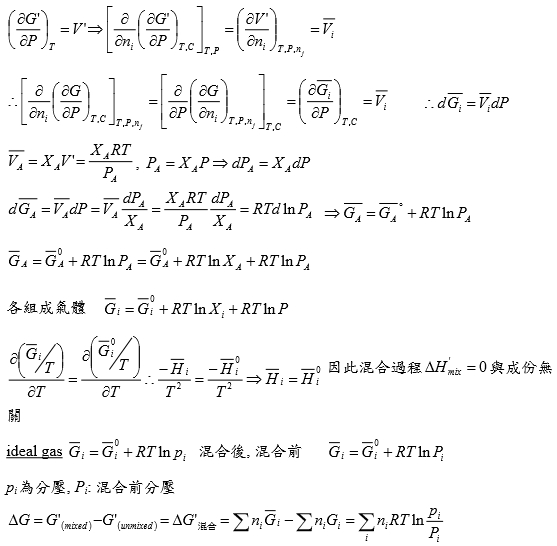



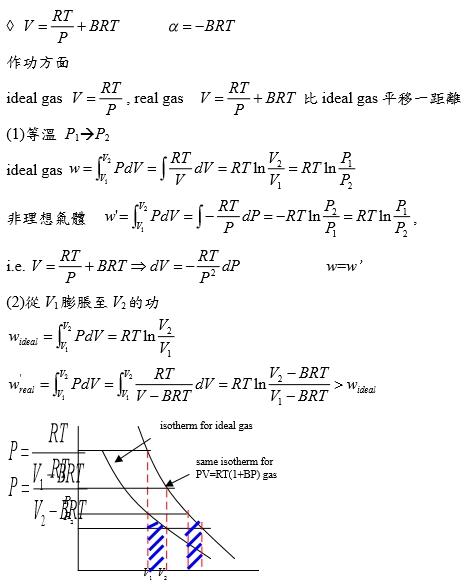
Chapter 8 The Behavior Of (non-ideal) Gases
*狀態方程式: V=RT/P ideal gas vs. V=f(T,P)=? real gas
*G-P關係: ideal gas dG=RTdlnP
non-ideal gas: fugacity(逸壓, f) → dG=RTdlnf, f≠P
P-V-T relationship limPV/RT --> 1 as P --> 0
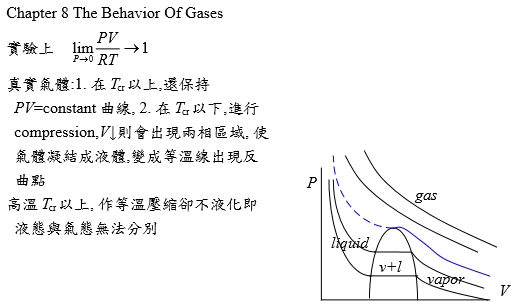
實驗上
真實氣體:1. 在Tcr以上,還保持PV=constant曲線, 2. 在Tcr以下,進行壓縮,V↓則會出現兩相區域, 使氣體凝結成液體,變成等溫線出現反曲點;高溫Tcr以上, 作等溫壓縮卻不液化即液態與氣態無法分別
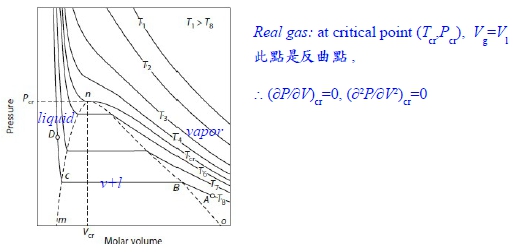
壓縮係數 Z=PV/RT ideal gas Z=1; real gas Z=1+?
在低壓下 0~10 atm 可表成Z=mP+1, m<0 font="" face="Times New Roman, serif">→ P(V-mRT)=RT or P(V-b’)=RT 式中b’不為粒子之体積, b’<0 font="" face="Symbol, serif">純粹為一實驗方程式(實驗走不通,換理論探討)
理論: Van der Waals gas
ideal gas特性: U=U(T), H=H(T), U=∑Eₖᵢ, 氣體分(原)子不佔體積,分(原)子間無作用力
修正:1. 氣体分子佔有体積, 2. 分子間有交互作用力
Van der Waals gas 方程式 (P+a/V²)(V-b)=RT

粒子間吸力使氣体壓力低於沒有吸力時之壓力所以(P+a/V2)當氣体視為理想時所作用之壓力
如何求 a=? b=? (實際值要靠實驗的Tcr, Pcr, Vcr)
當T=Tcr, P-V圖有反曲點: (∂P∕∂V)Tcr=0, (∂²P∕∂V²)Tcr=0
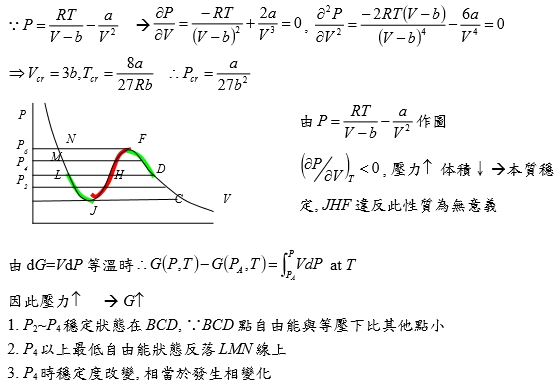
⸪P=RT/(V-b)-a/V² → (∂P∕∂V)=-RT/(V-b)²+2a/V³=0, (∂²P∕∂V²)=-2RT(V-b)/(V-b)⁴-6a/V⁴=0
→ Vcr=3b, Tcr=8a/27Rb ⸫Pcr=a/27b² or b=Tcr/8Pcr, a=9RTcrVcr/8=3PcrVcr²
V=f(T,P)=? 靠實驗量測, virial eq. Z=1+aP+bP²+cP³+...=1+a/V+b/V²+c/V³+...
結論: 當壓力不是很大,都看成理想氣體, PV=RT
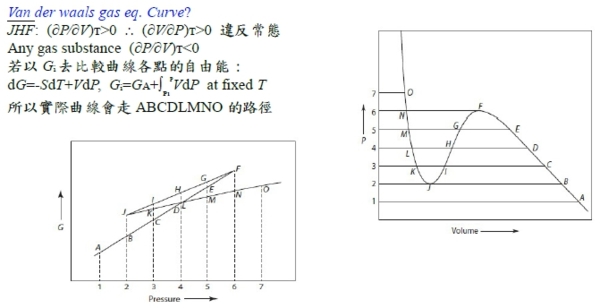
Vapor pressure of condensed liquid, Pₛₐₜ
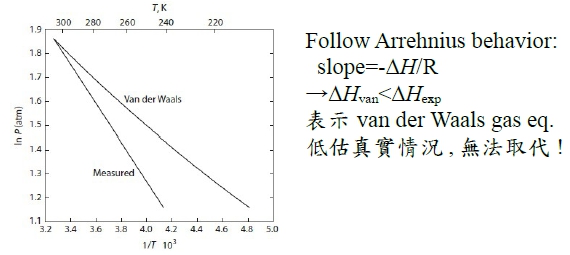
*當T →Tcr Hvap→0, proof by thermodynamics
l → g evaporation,Hvap=Hv-Hl=Uv-Ul+P(Vv-Vl) i.e. H≡U+PV
⸪dU=TdS-PdV → (∂U∕∂V)ᴛ=T(∂S∕∂V)ᴛ-P=T(∂P∕∂T)ᴠ-P, P=RT/(V-b)-a/V²→(∂P∕∂T)ᴠ=R/(V-b)代入上式 (∂U∕∂V)ᴛ= T[R/(V-b)]-P=P+a/V²-P= a/V² --> U=-a/V+constant
Hvap=Uv-Ul+P(Vv-Vl)=-a/Vv+a/Vl+P(Vv-Vl)
當T →Tcr ∵VvVl , Pv= Pl ⸫Hvap→0
Virial方程式 PV/RT=1+BP+CP²+... or PV/RT=1+B/V+C/V²+... 低壓時
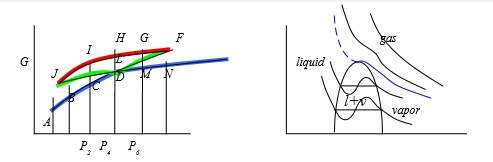
§氣體狀態改變時的G? dG=-SdT+VdP At fixed T, dG=VdP,
理想氣體dG=RTdP/P=RTdlnP, ⸫G(P₂,T)-G(P₁,T)=RTln(P₂/P₁), ∆G=RTln(P₂/P₁)
Real gas: fugacity, f逸壓, dG≡RTdlnf f≠P and f≤P; as P→0, 氣體趨近ideal gas, ⸫ f/P1
real gas 一氣體偏離ideal gas, 考慮gas滿足α=Vᵢᵈ-Vᵣᵉ=RT/P-V 方程式α=α(T)
定溫下dG=VdP=RTdlnf → VdP=RTdlnf → (RT/P-α)dP=RTdlnf
→ RTdlnP-RTdlnf=αdP → dln(f/P)=-αdP/RT → ln(f/P)=∫₀ᴾ-α/RTdP
溫度T, 在P=0~P=P之間ln(f/P)P=P-ln(f/P)P=0=-αP/RT i.e. ln(f/P)P=0=ln1=0
→ ln(f/P)=-αP/RT → f/P=e-αP/RT
if α<<1 span="">, e-αP/RT≈1- αP/RT ⸫f/P=1- αP/RT=1-(RT/P-V)P/RT=PV/RT
*calculate f from gas eq. Z=Z(P)=1+aP+bP²+cP³+...若氣體為ideal gas, P可視為RT/V, f/P=Pideal/P=1
dln(f/P)=-αdP/RT=(V/RT-1/P)dP= 1/P(PV/RT-1)dP=(Z-1)dP/P
ln(f/P)=∫₀ₚ(Z-1)dP/P 等溫下壓力改變, dG=VdP or dG=RTdlnf
e.g. N₂ at T=273.16K=0℃, PV=22414.6−10.281P + 0.065189P² + 5.1955×10⁻⁷P⁴−1.3156 ×10⁻¹¹P⁶+1.009×10⁻¹⁶P⁸=a+bP+cP²+nP⁴+eP⁶+gP⁸
Q1: when P=100 atm, f=?
Z=PV/RT=1/RT∙(a+bP+cP²+nP⁴+eP⁶+gP⁸)=1+1/RT∙(bP+cP²+nP⁴+eP⁶+gP⁸), RT=22414.6
→(Z-1)/P=1/RT∙(b + cP + nP³+eP⁵+gP⁷)
∫₀¹⁰⁰dln(f/P)=∫₀¹⁰⁰(Z-1)dP/P=1/RT∙(bP+cP²/2+nP⁴/4+eP⁶/6+gP⁸/8)
, ln(f/100)=...=-0.03084 ⸫ f=96.96≈97 atm when P=100 atm, 3% error only,
Q2: P change from 1 to 150 atm, check ∆Gᵢᵈ=?, ∆Gᵣᵉ=?
∆Gᵢᵈ= ∫₁¹⁵⁰RTdlnP=RTln(150/1)=112311 atmcm³=11373 J
∆Gᵣᵉ=∫RTdlnf=∫VdP=∫(a/P+b+cP+nP³+eP⁵+gP⁷)dP=alnP+bP+cP²/2+nP⁴/4+eP⁶/6+gP⁸/8)
=111490 atm∙cm³=11297J
∆Gᵢᵈ-∆Gᵣᵉ=76J, ~0.7% error
Topics: *given Z=1++aP+bP²+cP³+... 求 f=? ∆Gᵣᵉ=? ∆W=?
e.g. Z=PV/RT=1+BP, calculate ∆W by (i) P₁→P₂ (ii) V₁→V₂ (iii) compare with ∆Wᵢᵈ
(i) ideal gas ∆Wᵢᵈ=∫PdV=∫P(-RT/P²)dP=RTln(P₁/P₂), V=RT/P ⸫dV=(-RT/P²)dP
∆Wᵣᵉ=∫PdV=∫P(-RT/P²)dP=RTln(P₁/P₂), ⸪ V=RT(1+BP)/P→dV=(-RT/P²)dP
(ii) ∆Wᵢᵈ=∫PdV=∫(RT/V)dV=RTln(V₂/V₁), ∆Wᵣᵉ=∫PdV=∫RT/(V-BRT)dV=RTln[(V₂-BRT)/(V₁-BRT)]
⸪ PV/RT=1+BP→P(V/RT-B)=1→ P=RT/(V-BRT)
Ex. 假設氣體遵守PV/RT=Z=1+BP+CP²+... Virial方程式 → V=RT(1/P+B+CP+DP²)
ΔG=∫ᴘ₁ᴘ₂VdP=∫RT(1/P+B+CP+DP²+...)dP=RT[ln(P₁/P₂)+B(P₂-P₁)+C/2(P₂²-P₁²)+D/3(P₂³-P₁³)]
if ideal gas, dG=RTln(P₁/P₂)
非理想氣體之額外自由能變化=RT[B(P₂-P₁)+C/2(P₂²-P₁²)+D/3(P₂³-P₁³)]
ln(f/P)=∫₀ₚ(Z-1)dP/P =∫₀ₚ(B+CP+DP²+...)dP=BP+CP²/2+DP³/3+...
⸪dG=RTdlnf → dG=RTdlnf/P+ RTdlnP
ΔG=RT[B(P₂-P₁)+C/2(P₂²-P₁²)+D/3(P₂³-P₁³)]+RTln(P₁/P₂)
real gas:
(1)Virial function PV/RT=1 in 0~6 atm,
(2)PV/RT=1+BP in 0~20 atm → V=RT/P+BRT → α=-BRT
作功方面
ideal gas: V=RT/P, real gas: V=RT/P+BRT 比ideal gas平移一距離
(1)等溫 P1P2
ideal gas w=∫ᴠ₁ᴠ₂PdV=∫RTdV/V=RTln(V₂/V₁)=RTln(P₁/P₂)
非理想氣體 w=∫ᴠ₁ᴠ₂PdV=∫-RTdP/P=-RTln(P₂/P₁)=RTln(P₁/P₂), i.e. V=RT/P+BRT → dV=-RTdP/P²
(2)從V1膨脹至V2的功
wᵢᵈₑₐₗ=∫ᴠ₁ᴠ₂PdV=RTln(V₂/V₁) vs. wᵣₑₐₗ=∫ᴠ₁ᴠ₂PdV=∫ᴠ₁ᴠ₂RTdV/(V-BRT)=RTln[(V₂-BRT)/(V₁-BRT)]>wᵢᵈₑₐₗ
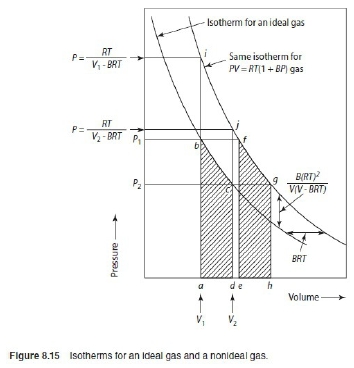
氣體方程式: ideal gas PV=RT, van der Waals gas (P+a/V²)(V-b)=RT,
virial eq. Z=PV/RT=1+aP+bP²+cP³+... or Z=PV/RT=1+a/V+b/V²+c/V³+...
Ex-1. 1 mole N₂ 氣體方程式: P=RT/(V-b)-a²/V², a=1.39 b=39.1
Q: at 400K, V₁=1 l → V₂=2 l ∆G=?, ∆S=?
∆G=∫₁²dG=∫ᴘ₁ᴘ₂VdP=∫ᴠ₁ᴠ₂?dV, ⸪ P=RT/(V-b)-a²/V²
→ dP=[R/(V-b)]dT-[RT/(V-b)²]dV+2a²/V³→ dP=[R/(V-b)]dT+[2a²/V³-RT/(V-b)²]dV
at fixed T, ∆G=∫dG=∫VdP=∫V[2a²/V³-RT/(V-b)²]dV=-2a²/V-∫V RT/(V-b)²]dV
i.e. let V-b=x, dV=dx → ∫V RT/(V-b)²]dV=∫RT(x+b)/x²]dx=∫(RT/x)dx+∫(RTb/x²)dx
⸫ ∆G=-2a²/V+RTln(V-b)-RTb/(V-b)代入a, b, T, V₁, V₂ ∆G=-2636J
∆S=? S=S(T,V) 2nd TdS eq. dS=(cᵥ/T)dT+(α/β)dV 但不一定記得!
dS=(∂S∕∂T)ᵥdT+(∂S∕∂V)ᴛdV=(∂S∕∂V)ᴛdV=(∂P∕∂T)ᵥdV at fixed T
(∂P∕∂T)ᵥ=R/(V-b) ⸪ dP=[R/(V-b)]dT+[2a²/V³-RT/(V-b)²]dV
∆S=∫dS=∫(∂P∕∂T)ᵥdV=∫[R/(V-b)]dV=Rln[(V₂-b)/(V₁-b)]=5.93
Ex-2. 異丁烷氣體: Z=1+A/V+B/V² A=-265, B=30250
Q: at 460K, V₁=400 c.c. → V₂=200 c.c. ∆G=?
∆G=∫dG=∫-SdT+VdP=∫VdP=∫?dV
Z=1+A/V+B/V²=PV/RT → P=RT(1/V+A/V²+B/V³) → dP=RT(-1/V²-2A/V³-3B/V⁴)dV代入上式
∆G=∫VdP=∫V∙RT(-1/V²-2A/V³-3B/V⁴)dV=-RT[lnV-2A/V-3B/2V²]=838J
Q2: P₁=50 atm → P₂=100 atm, ∆W=?
∆W=∫δW=∫PdV=∫RT(1/V+A/V²+B/V³)dV=RT(lnV-A/V-B/2V²)
P₁, P₂代入Z=1+A/V+B/V²=PV/RT得V₁=394.6 c.c., V₂=176.9 c.c. 代入積分 ∆W=-1384J
**在題目中由氣體方程式找dP=....dT+....dV的關係或是P=P(T,V)


