Chapter 7 Phase Equilibria In A One Component System
系統的内涵性質,另一類勢的測量, ex. 溫度、壓力、化學勢…
1. 溫度: 系統内勢or熱強度一種測量
熱離開系統的傾向, 例如高溫→低熱,有一gradient存在,直到熱流消失,溫度相等,熱平衡為止。
2. 壓力: 系統内質量移動的傾向
ex. 相之間有淨壓力時,質量移動使壓力gradient抵消, 使系統内不同部份,壓力彼此相等。
3. 一相內的成分(component) i的化學勢
測量成分i離開該相的傾向大小;種類i傾向從高化學勢的相移出而轉入較低化學勢的相。”potential gradient” 化學擴散的驅動力,直到化學勢μi在不同的相均相等,平衡才成立。
dG=-SdT+VdP+∑μᵢdnᵢ
材料熱力學從能量的觀點,探討物質的變化
§thermodynamic equilibrium, e.g. α, and β phases co-existed at fixed T, P
thermal equil. Tα=Tβ , mechanical equil. Pα=Pβ, chemical equil. μα=μβ
at equilibrium, G=Gₘᵢₙ ← dG=0 ⸪ G≡H-TS 欲知G(T)=? H(T)=? S(T)=? at P(=1 atm) 進一步了解 Gα(T)=? Gβ(T)=?
at T=T₀, if Gα(T₀)<Gβ(T₀), reaction: β→α, α stable.
If Gα(T₀)=Gβ(T₀), reaction: β↔α, α+β phases co-existed, T₀:相轉換溫度
7-2 研究G-T-P的關係式來討論平衡
若維持在1atm, 0℃時冰水平衡 H₂O₍ₗ₎ ↔ H₂O₍ₛ₎ at 1atm, 273K
T>273K, Gᴴ₂ᴼ₍ₛ₎>Gᴴ₂ᴼ₍ₗ₎ liquid stable.
T=273K, Gᴴ₂ᴼ₍ₛ₎=Gᴴ₂ᴼ₍ₗ₎ liquid+solid stable. ←討論點!
T<273K, Gᴴ₂ᴼ₍ₛ₎<Gᴴ₂ᴼ₍ₗ₎ solid stable.
若含nₛ mole水和nₗ mole冰: G=nₛGᴴ₂ᴼ₍ₛ₎+nₗGᴴ₂ᴼ₍ₗ₎=contant at Tₘ, 其冰水比例無關(i.e. nₛ+nₗ=c)
可以說: 平衡時, H2O從液相中脫離傾向等於固相中的脫離傾向。
定溫定壓下, Gᵀ,ᴾ=μₛnₛ+μₗnₗ→比較G=nₛGᴴ₂ᴼ₍ₛ₎+nₗGᴴ₂ᴼ₍ₗ₎ vs. Gᵀ,ᴾ=μₛnₛ+μₗnₗ
molar Gibbs free energy, μᵢ≡(∂G∕∂nᵢ)ᴛ,ᴘ,nj=Gᵢ
如何求Gᴴ₂ᴼ₍ₛ₎(T), Gᴴ₂ᴼ₍ₗ₎(T)? given: cₚ₍ₛ₎=38J/Kmole, cₚ₍ₗ₎=75.44J/Kmole, ∆Hₘ=6008J/mole. At 298K, H₍ₛ₎=-6944, S₍ₛ₎=44.77; H₍ₗ₎=0, S₍ₗ₎=70.08
通式: H(T)=H₂₉₈+∫₂₉₈ᵀcₚdT, S(T)=S₂₉₈+∫₂₉₈ᵀ(cₚ/T)dT → H₍ₛ₎(T)=..., S₍ₛ₎(T)=..., H₍ₗ₎(T)=..., S₍ₗ₎(T)=...
→ Gᴴ₂ᴼ₍ₛ₎(T)=H₍ₛ₎(T)-TS₍ₛ₎(T)=f₍ₛ₎(T), Gᴴ₂ᴼ₍ₗ₎(T)=H₍ₗ₎(T)-TS₍ₗ₎(T)=f₍ₗ₎(T)
1. 求ΔH, let H298(l)=0
H₍ₗ₎,ᴛ=∫₂₉₈ᵀcₚ₍ₗ₎dT=75.44(T-298)=75.44T-22481,
H₍ₛ₎,ᴛ=∫₂₉₈²⁷³cₚ₍ₗ₎dT-ΔHₘ+∫₂₇₃ᵀcₚ₍ₛ₎dT=75.44(273-298)-6008+38(T-273)=38T-18268
ΔHᴛ=H₍ₗ₎,ᴛ-H₍ₛ₎,ᴛ=75.44(T-298)-75.44(273-298)+ΔHₘ-38(T-273)=37.44T+4231.12
2. TΔS
S₍ₗ₎,ᴛ=S₍ₗ₎,₂₉₈+∫₂₉₈ᵀcₚ₍ₗ₎dlnT=70.08+75.44ln(T/298),
S₍ₛ₎,ᴛ=S₍ₛ₎,₂₉₈+∫₂₉₈ᵀcₚ₍ₛ₎dlnT=44.77+38ln(T/298)
ΔS=S₍ₗ₎,ᴛ-S₍ₛ₎,ᴛ=25.31+37.44ln(T/298)
As ΔH₍ₛ→ₗ₎= Tm ΔS₍ₛ→ₗ₎ → 37.44T+4231.12=25.31T+37.44Tln(T/298)→ Tm=?
3. Gᴴ₂ᴼ₍ₛ₎(T)=H₍ₛ₎(T)-TS₍ₛ₎(T)=38T-18268-T[44.77+38ln(T/298)]=18268-6.77T+38Tln(T/298)
Gᴴ₂ᴼ₍ₗ₎(T)=H₍ₗ₎(T)-TS₍ₗ₎(T)= 75.44T-22481-T[70.08+75.44ln(T/298)]=22481+5.36T+75.44Tln(T/298)
ΔG(T)=Gᴴ₂ᴼ₍ₗ₎(T)-Gᴴ₂ᴼ₍ₛ₎(T)=4213+12.13T+37.44Tln(T/298)
as T<0℃, Gᴴ₂ᴼ₍ₛ₎<Gᴴ₂ᴼ₍ₗ₎ solid stable;
T=0℃, liquid+solid stable.(melting point)
consider s → l ∆G=Gₗ-Gₛ
(i) T<Tₘ, ∆G>0
(ii) T=Tₘ, ∆G=0
(iii) T>Tₘ, ∆G<0
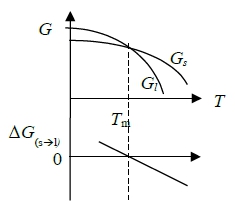
重點討論 ∆G? ∆G<0, reaction! (Any transformation)
∆G=∆H-T∆S at Tₘ, ∆H=∆Hₘ>0 and ∆S=∆Sₘ>0 表示溫度上升,∆G會下降(S contribution is more important at high temperature.)
G(T), ∆G(T)的curve shape? 採monotonic change
⸪ dG=-SdT+VdP (∂G∕∂T)ₚ=-S<0代表函數的斜率, (∂²G∕∂T²)ₚ=-(∂S∕∂T)ₚ=-cₚ/T<0代表函數的曲率
e.g. s → l ∆Gₛₗ=∆Gₘ=Gₗ-Gₛ (∂∆Gₘ∕∂T)ₚ=-∆Sₘ<0, (∂²∆Gₘ∕∂T²)ₚ=-(∂∆Sₘ∕∂T)ₚ→0 *Richards rule ∆Sₘ=c₀
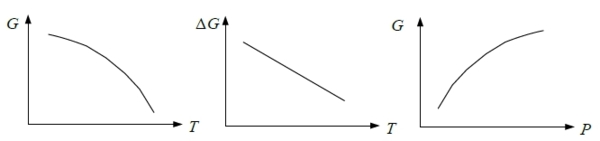
G(P), ∆G(P)的curve shape?
At fixed T, (∂G∕∂P)ᴛ=V>0斜率, (∂²G∕∂P²)ᴛ =(∂V∕∂P)ᴛ =-βV<0曲率
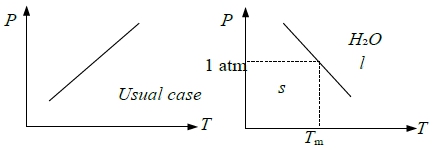
e.g. s → l (∂∆G∕∂P)ᴛ=∆V=Vₗ-Vₛ>0 usual cases, but ∆V=Vₗ-Vₛ<0 for H₂O
(∂²∆G∕∂P²)ᴛ=(∂∆V∕∂P)ᴛ=-(βₗVₗ-βₛVₛ)→0
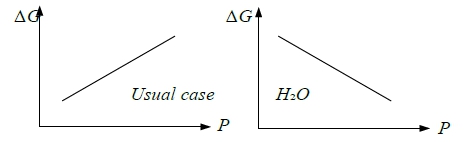
§Phase equilibrium(transformation) T(P)?
e.g. s → l Tₘ(P)=? or l → g Tᵇ(P)=? consider s ↔ l Gₗ=Gₛ at Tₘ ⸫ dGₗ=dGₛ
dGₛ=-SₛdT+VₛdP, dGₗ=-SₗdT+VₗdP → d(Gₗ-Gₛ)=-(Sₗ-Sₛ)dT+(Vₗ-Vₛ)dP → d∆G=-∆SdT+∆VdP
⸪∆G=0 at Tₘ, -∆SdT+∆VdP=0
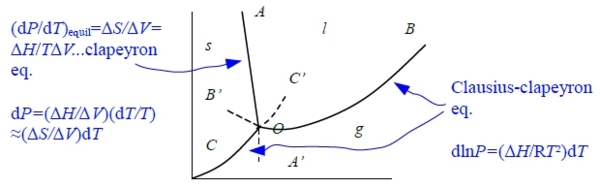
⸫ (dP/dT)ₑզᵤᵢₗ=∆Sₘ/∆V=∆Hₘ/Tₘ∆V...clapeyron eq. i.e. ∆Gₘ=∆Hₘ-Tₘ∆Sₘ
e.g. s → l for H₂O, ∆Hₛₗ>0, ∆Sₛₗ>0but ∆V=Vₗ-Vₛ<0 ⸫ (dP/dT)<0 P↑ 則Tₘ↓ 例如溜冰時體重施在冰上的壓力會使冰溶化(從理論上冰會因壓力上升而融化,但實際上加壓為瞬間,並未發現冰鞋有水,可能與冰的表面情況有關)
condensed phase transition, α ↔ β Tαβ(P) ?
Clapeyron Eq. (dP/dT)ₑզᵤᵢₗ=∆S/∆V=∆H/T∆V, ∆V=Vβ-Vα, ∆S=Sβ-Sα
∫₁ᴾdP=∫ᴛₘᵀ(∆S/∆V)dT≈(∆S/∆V)(T-Tₘ),
e.g. ∆Sₘ>0 and ∆V=Vₗ-Vₛ <0 for H₂O, but ∆V>0 for usual cases.
§solid(liquid) ↔ vapor(gas) phase transition
(dP/dT)ₑզᵤᵢₗ=∆S/∆V=∆H/T∆V, ∆V=Vg-Vs≡Vg or Vg-Vl≈ Vg=RT/P
→ (dP/dT)≈∆H/TVg=P∆H/RT² → dlnP=(∆H/RT²)dT...clausius-clapeyron eq.
積分→ ∫₀ᴾdlnP=∫ᴛᵇᵀ(∆H/RT²)dT → lnP=? f(T)
e.g. l → g given: ∆Hᵇ, Tᵇ ; ∆H(T)=∆Hᵇ+∫ᴛᵇᵀ∆cₚdT, ∆cₚ=cₚ,g-cₚ,l=f(T)=? ∆cₚ=∆a+∆bT+∆c/T²
a. ∆H=∆Hᵇ , if ∆cₚ=0 → lnP=-∆Hᵇ/R(1/T-1/Tᵇ)=-∆Hᵇ/RT+c₀ ⸫ lnP=-∆Hᵇ/RT
b. ∆cₚ=∆a=c₀ 常數, ∆H=∆Hᵇ+c₀(T-Tᵇ) → lnP=∫ᴛᵇᵀ([∆Hᵇ+c₀(T-Tᵇ)]/RT²)dT= (c₀Tᵇ -∆Hᵇ)/RT+(c₀/R)lnT+C₀ ⸫ lnP=A₀/T+B₀lnT+C₀, i.e. ∆H=(∆Hᵇ-c₀Tᵇ )+c₀T
c. ∆cₚ=∆a+∆bT+∆c/T²
e.g. H₂O, cₚ,l=75.44, cₚ,g=30+10.7∙10⁻³T+0.33∙10⁵T⁻², Tᵇ=373K, ∆Hᵇ=41090J
求P(T)... vapor pressure of water(l → g)
∆H(T)=∆Hᵇ+∫ᴛᵇᵀ∆cₚdT=41090+∫ᴛᵇᵀ (-45.44+10.7∙10⁻³T+0.33∙10⁵T⁻²)dT=(41090+45.44∙373-5.35∙10⁻³ 373²+0.33∙10⁵/373)-45.44T+5.35∙10⁻³T²-0.33∙10⁵/T 代入∫₀ᴾdlnP=∫ᴛᵇᵀ(∆H/RT²)dT
lnP=-52383/RT-45.44lnT/R+5.35∙10⁻³T/R+0.33∙10⁵/2RT²+51.1
ex. cₚ,H₂O₍ᵥ₎=30+10.7∙10⁻³T+0.33∙10⁵T⁻² , 298~2500K; cₚ,H₂O₍ₗ₎=75.44, 273~373, Hᵥ=41090
ΔHᴛ=ΔH₃₇₃+∫₃₇₃ᵀ∆cₚ₍ₗ→ᵥ₎dT, dlnP=(ΔH/RT²)dT
→ lnP=-58872/RT-(45.44/R)lnT+(5.35∙10⁻³/R)T+(0.33∙10⁵/2R)T⁻²+C,
B.C.: P(373K)=1 atm 求C=?(51.092)
固液相平衡dP/dT=ΔHf/TΔVf , 斜率AOA’ dP/dT=PΔH/RT²*OA’對 gas為介穩態,在相同的 T, P 下,有較高的G值
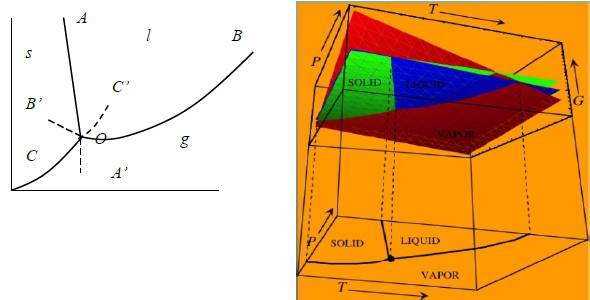
一元三相圖中如何畫G-T, G-P變化曲線?
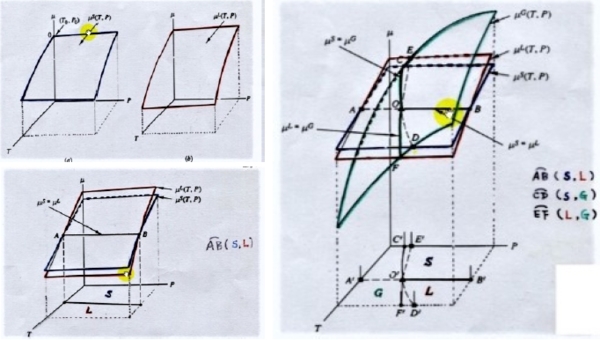
G-T curves at fixed P:
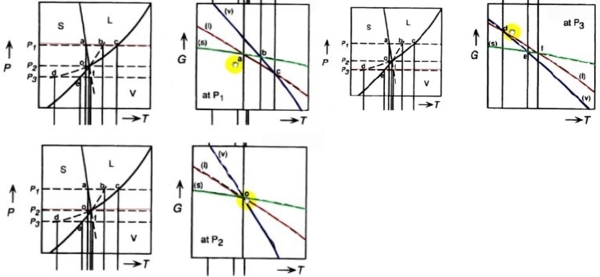
G-P curves at fixed T:
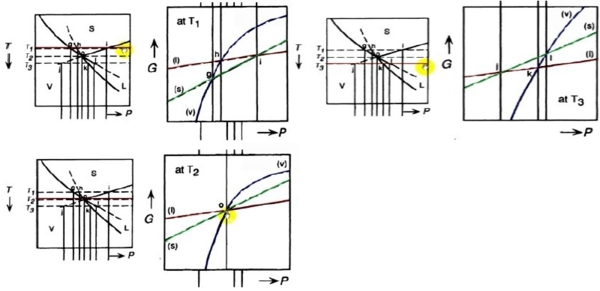
solid phase transition: e.g. Fe: α(BCC) → γ(FCC) → δ(BCC) → l different crystal structures: allotropes同素異形體, compound ZrO₂: monoclinic → tetragonal → cubic → l, polymorphism多形體
補充: slope of phase change, α ↔ β
e.g. Fe α(BCC) → γ(FCC) ∆V=V(FCC)-V(BCC)<0 ⸫ (dP/dT)ₑզᵤᵢₗ=∆S/∆V<0
γ(FCC) → δ(BCC) ∆V=V(BCC)-V(FCC)>0 ⸫ (dP/dT)ₑզᵤᵢₗ=∆S/∆V>0
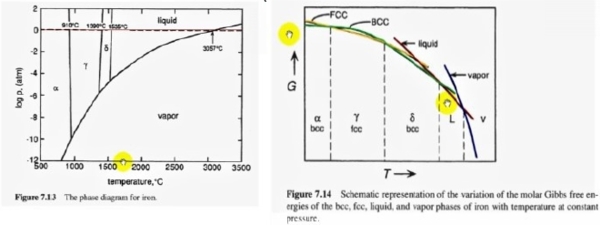
phase diagram:
for l → g logPₗ=A/T+BlogT+C, s → g logPₛ=A/T+BlogT+C
at triple point, Pₗ=Pₛ → A/T+BlogT+C=A/T+BlogT+C
Gibbs Phase rule f=c-P+2
e.g. one component, c=1⸫ f=3-P (I) one phase region: P=1 → f=2 (ii) two phases curve: P=2 → f=1 (iii) 3 phaes coexist: P=3 → f=0 (triple point)
該系統有P個相, C個chemical species; 前提(1)沒有化學反應發生, (2)每種成分在每一相均存在. 根據(2), 有PC個mole fractions, 再加上T, P → PC+2 intensive variables.
a. 在每相中,例如α相中 x₁α+x₂α+x₃α+x₄α+...+xᶜα=1,∵有P個相有P個方程式, 可限制P個變數
b. 在各相間同種的μi要平衡時均相同
μ₁α=μ₁β=μ₁γ=..., μ₂α=μ₂β=μ₂γ=..., μᶜα=μᶜβ=μᶜγ=...有P-1個等式共有C(P-1) 個方程式
→f=PC+2-P-C(P-1)=C-P+2
在兩相存在區, OA線 or OB, OC線: f=1-2+2=1個自由度(P或T)→ P固定, T即固定。
三相點→ f=1-3+2=0
Ex=1. NaF s → g lnPₛ=-34450/T-2.01lnT+33.74...(1)
l → g lnPₗ=-31090/T-2.52lnT+34.66...(2)
Q1: Tᵇ=? Boiling at P=1 atm
Pₗ=1 atm, ln1=0=-31090/T-2.52lnT+34.66 Tᵇ=2006K
Q2: Tₜ=? Pₜ=?
Pₛ=Pₗ, (1)=(2), -34450/T-2.01lnT+33.74=-31090/T-2.52lnT+34.66, -3360/T+0.51lnT-0.92=0 Tₜ=1239K代入(1)或(2), Pₜ=2.29∙10⁻⁴ atm
Q3: ∆Hᵇ=?
∵ dlnP=(∆H/RT²)dT → ∆Hᵇ=RT²(dlnPₗ/dT)=RT²[31090/T²-2.52/T]=258500-20.95T=216500J
Q4: when T=Tₜ, ∆Hₛₗ=?
∆Hₛₗ=Hₗ-Hₛ=Hₗ-Hg+Hg-Hₛ=-(Hg-Hₗ)+(Hg-Hₛ)=-∆Hₗg+∆Hₛg, ∆Hₗg=∆Hᵇ= 258500-20.95T, ∆Hₛg=RT²(dlnPₛ/dT)=RT²[34450/T²-2.01/T]=286417-16.71T
∆Hₛₗ=-( 258500-20.95T)+286417-16.71T=27917+4.24T=33170J
Q5: ∆cₚ=cₚ₍ₗ₎-cₚ₍ₛ₎=?
∆H(T)=∆H(T₀)+∫ᴛ₀ᵀ∆cₚdT ↔ ∆cₚ=(d∆H/dT)=4.24
Ex-2. cabon(graphite) → diamond at 298K, P≥?
Given: Hᴅ=1900J/mole, Sg=5.73J/Kmole, Sᴅ=2.43J/Kmole, ρg=2.22g/cm³, ρᴅ=3.515g/cm³
concept: at fixed T, how much P is big enough to make reaction spontaneous(∆G≤0)?
dG=-SdT+VdP, (∂∆G∕∂P)ᴛ=∆V, ∆G=Gᴅ-Gg=(Hᴅ-Hg)-T(Sᴅ-Sg)=(1900-0)-298(2.43-5.73)=2883J
at fixed T, ∫₂₈₈₃⁰d∆G=∫₁ᴾ∆VdP ∆G₀-2883=∆V(P-1)=(M/ρᴅ-M/ρg)(P-1)=-1.99(P-1)∙0.101
∆G₀=-0.201138(P-1)+2883≤0, P≥14334 atm