《先備知識》
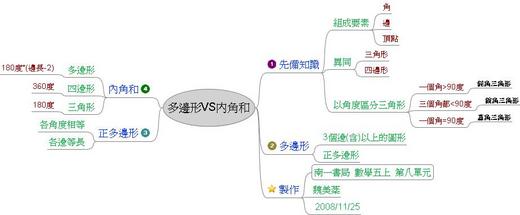
幾何圖形的組成要素：頂點、邊、角，知道邊數與頂點、角之間的關係；辨別三角形與四邊形的異同；三角形依據不同的角度會有不同的稱呼：銳角三角形、鈍腳三角形、直角三角形。

《基本概念》
多邊形也就是具有三個邊(含)以上的圖形，可以認識不同圖形所代表的名稱。
正多邊形則是具有每個邊長等長、角度一樣、具有相同數量的頂點的多邊形。
內角和則是多邊形裡面所有的角度總和。公式則是=180度*(邊數-2)。
個別的內角則可以利用刪去減法求出未知的角度，如果是正多邊形則只需要除以邊數就可以得到。

《教學解析》
先以三角形的角度出發，將一個三角形的各角剪下排列，可以發現這三個角合成180度的平面。由此我們可以知道三角形的內角和等於180度。再透過圖形的觀察，發現四邊形可以化成2個三角形，也就是內角和=2*180度；五邊形可以化成3個三角形，內角和=3*180度；六邊形可以化成4個三角形，4*180度，以此類推，可以發現邊長與三角形之間的關係，就可以得到公式=180度*(邊長-2)。

單獨角度的求取則是利用已知的內角和再依序減去已知的角度，就可以求出未知的角度。如果內角和不曉得則必須先將內角和計算出來，再做減法的運算。正多邊形的內角則是=內角和/邊長，即可得到所需要的角度。

《常見題型》
1.辨識圖形。
2.寫出圖形名稱。
3.寫出圖形的特徵(頂點、角、邊長)
4.算出三角形的角度，或是內角和。
5.算出四邊形、五邊形、六邊形等多邊形的內角或內角和。