引用文章１８８４年ＳＡＮＧＡＫＵ問題

圖一

（１）
如圖１，作△ＫＯＧ～（全等於）△ＣＱＥ～△ＤＣＧ
　　　　作△ＮＰＧ～（全等於）△ＲＦＥ～△ＪＦＧ
　　　　得∠１＝∠４，∠３＝∠６。ＫＧ＝ＱＥ、ＮＧ＝ＲＥ
連接ＯＰ、ＱＲ、ＣＦ

（２）
易証△ＰＯＧ～△ＣＥＦ（ＳＡＳ）
又∵　∠１＝∠４，∠３＝∠６
∴得　∠２＝∠５
又∵　ＫＧ＝ＱＥ、ＮＧ＝ＲＥ
∴　△ＫＮＧ（綠色三角形）～△ＱＲＥ（綠色三角形）（ＳＡＳ）
故　五邊形ＫＯＧＰＮ～五邊形ＱＣＥＦＲ
如圖２所示

圖２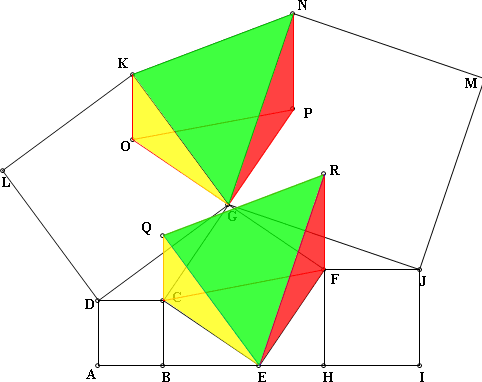

（３）
故　五邊形ＫＯＧＰＮ－△ＰＯＧ＝五邊形ＱＣＥＦＲ－△ＣＥＦ
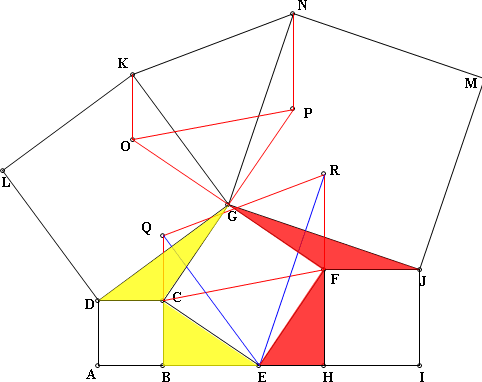
即　梯形ＫＯＰＮ＝梯形ＱＣＦＲ（藍色梯形）
且　梯形ＱＣＦＲ面積＝梯形ＣＢＦＨ面積（等上下底、同高）
得　梯形ＫＯＰＮ面積（藍色梯形）＝梯形ＣＢＦＨ面積（粉色梯形）（遞移律）
如圖三所示

圖三

（４）
又　△ＤＣＧ＝△ＣＢＥ＝△ＥＦＨ＝△ＧＦＪ（等底等高）
如圖四所示

圖四

∴　梯形ＫＯＰＮ面積＋△ＰＯＧ＝△ＧＣＦ＋梯形ＣＢＦＨ面積
即　五邊形ＫＯＧＰＮ＝五邊形ＧＣＢＨＦ
如圖五所示

圖五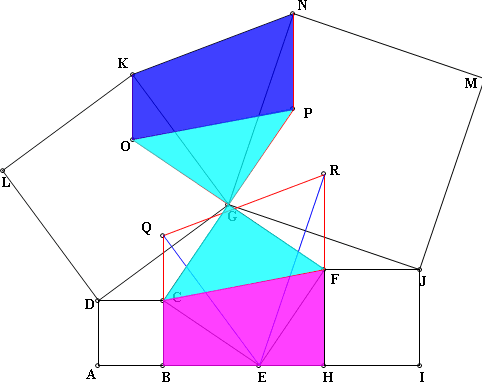

（５）
如圖六所示
故　△ＫＮＧ＝五邊形ＫＯＧＰＮ－△ＫＮＧ－△ＮＰＧ
　　　　　　＝五邊形ＧＣＢＨＦ－△ＣＢＥ－△ＥＦＨ
　　　　　　＝正方形ＣＥＦＧ

Ｑ.Ｅ.Ｄ.

圖六