宏本身也可以使用自已，遞回在MetaPost中是可以的。要注意不要形成無窮遞回，所以需要用條件式來控制。這是 Learning MetaPost by Doing 內的例子：

beginfig(1);

u:=2cm; branchrotation=60;

offset:=180-branchrotation;

thinning:=0.7;

shortening:=0.8;

def drawit(expr p, linethickness) = draw p withpen pencircle scaled linethickness; enddef;

vardef tree(expr A, B, n, size) =

save C, D, thickness; pair C, D;

thickness:=size;

C:=shortening[B, A rotatedaround(B, offset + uniformdeviate(branchrotation))];

D:=shortening[B,A rotatedaround(B, -offset-uniformdeviate(branchrotation))];

if n>0:

drawit (A--B, thickness);

thickness:=thinning*thickness;

tree(B, C, n-1, thickness);

tree(B, D, n-1, thickness);

else:

drawit(A--B, thickness);

thickness:=thinning*thickness;

drawit(B--C, thickness);

drawit(B--D, thickness);

fi;

enddef;

tree((0,0), (0, u), 10, 8mm);

endfig;

end;

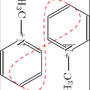
結果如下：

tree()主要目的就是畫出一條直線(A--B)加上二條分枝(B--C), (B--D)。其中 A rotatedaround( B, degree) 就是把A以B為圓心繞行degree度的pair值。這個pair值再乘上shortenning，所以它距B的距離就會縮短。分枝的寛度則乘上thinning。uniformdeviate是一個運算元，它可產生0到1中間的任意數值。

另外一個是畫出冰花。

u=3cm;

vardef koch(expr A, B, n)=

save C; pair C;

C:=A rotatedaround(1/3[A, B],120);

if n>1:

koch(A, 1/3[A,B], n-1);

koch(1/3[A,B], C, n-1);

koch(C, 2/3[A,B], n-1);

koch(2/3[A,B], B, n-1);

else:

draw A--1/3[A,B]--C--2/3[A,B]--B;

fi

enddef;

beginfig(1);

z0=(u, 0);

z1=z0 rotated 120;

z2=z1 rotated 120;

koch(z0, z1, 2);

koch(z1, z2, 3);

koch(z3, z0, 4);

endfig;

end;

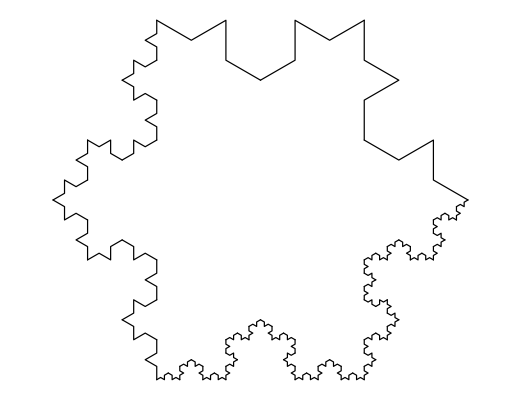
結果如下：