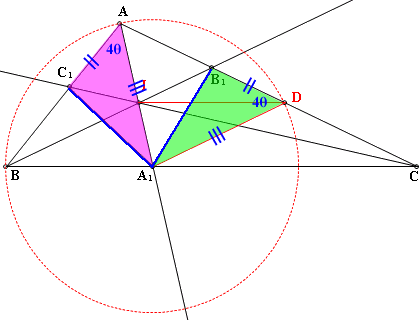
方法２：轉換線段比

（１）作輔助線

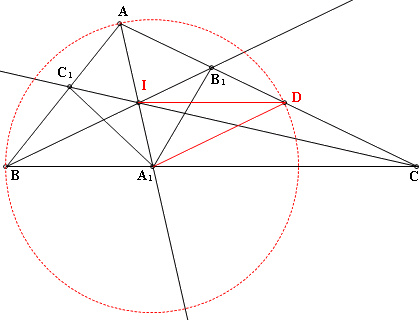
（２）證明全等

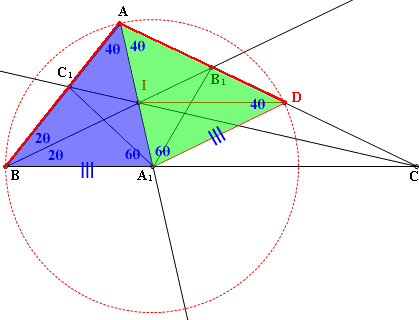
在△Ａ₁ＡＢ和△Ａ₁ＡＤ中
∵Ａ₁Ａ＝Ａ₁Ｄ
∴∠Ａ₁ＤＡ＝∠Ａ₁ＡＤ＝４θ

∵∠Ａ₁ＢＡ＝∠Ａ₁ＤＡ＝４θ＝∠Ａ₁ＡＢ＝∠Ａ₁ＡＤ
且Ａ₁Ａ＝Ａ₁Ａ（共用）
∴△Ａ₁ＡＢ≡△Ａ₁ＡＤ（ＡＡＳ）
得ＡＢ＝ＡＤ

（３）證明平行

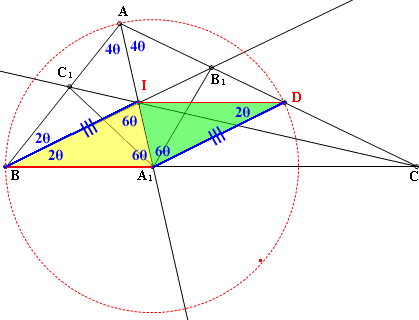
（４）ＡＢ₁：Ｂ₁Ｄ＝ＡＩ：ＩＡ₁

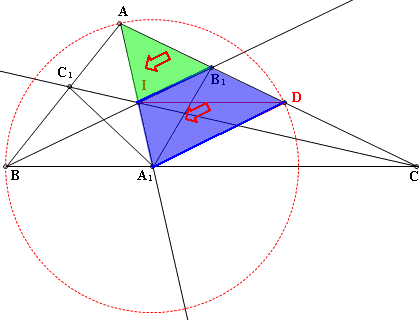
（５）ＡＩ：ＩＡ₁＝ＣＡ：ＣＡ₁

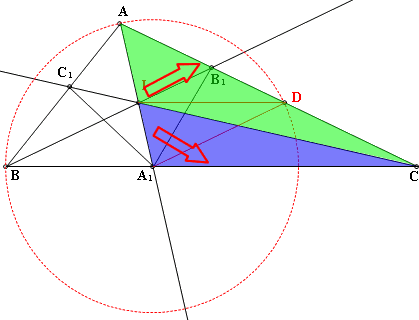
（６）ＢＣ₁：Ｃ₁Ａ＝ＢＣ：ＣＡ

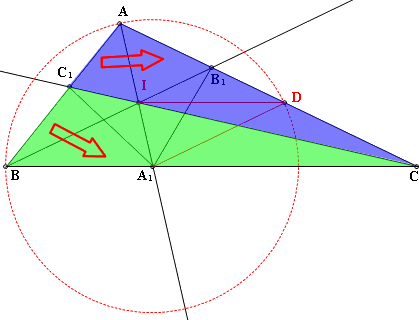
又△ＡＢＣ～和△ＡＡ₁Ｃ（ＡＡ相似）

故ＢＣ：Ｃ＝ＡＣＡ：ＣＡ₁

也就是ＢＣ₁：Ｃ₁Ａ＝ＡＢ₁：Ｂ₁Ｄ

又ＡＢ＝ＡＤ，∴Ｃ₁Ａ＝Ｂ₁Ｄ