Chapter 4 The Statistical Interpretation Of Entropy統計熱力學

古典熱力講巨觀,例如U, S的物理意義,抽象難以了解;Gibbs說: 熵為測量系統混合的程度，混合程度高→熵值大,但為何是『亂度』呢? 微觀下,1 mole=610²³ atoms, 1 cm³≈1 mole 也就是1 c.c.約有10²³個粒子的行為像機率分佈一樣, 而機率最大、最可能的狀態即表現在巨觀上

entropy(S)↔atomic scale “disorder”

Gibbs: S is degree of “mixed-upness” at atomic/molecular scale. 亂度, 熵

e.g. S_(ₛ)<S_(ₗ)<<S_(ᵍ), l → s at Tₘ ∆S_ᶠ=S_(ₛ)-S_(ₗ)<0, melting="" font="">s → l ∆Sₘ=∆Hₘ/Tₘ ∆Hₘ>0 ⸫∆Sₘ>0

l ↔ s at equilibrium ∆Sₘ=0

(1)過冷凝結: 雖然系統亂度下降，但熵卻增加；因為熱儲的亂度增加比系統亂度下降量要大。

(2)平衡凝固點: 總有序度未改變，亂度僅是從系統傳至熱儲，並無增熵，所以為可逆相變化。

“一系統平衡狀態為該系統最可能出現的狀態”，最有可能的微觀狀態決定巨觀平衡狀態

微觀與巨觀狀態的關係: 微觀分布(統計熱力學)↔巨觀(最可能的狀態)

量子理論:能階概念與尺寸有關(e.g. 一維長度決定共振(駐波)的頻率),體積牽涉到微觀的能階,巨觀狀態牽涉微觀的最可能分布

Determination of most probable microstates

當平衡時, Ω=Ω_mₐₓ,

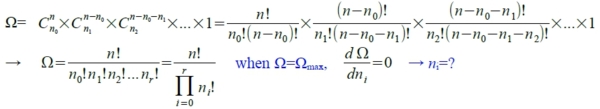
數目龐大,取ln 再處理(Sterling approximation: lnX!≈XlnX-X)

⸫ lnΩ=(nlnn-n)-[(n₀lnn₀-n₀)+(n₁lnn₁-n₁)+...+(nᵣlnnᵣ-nᵣ)]=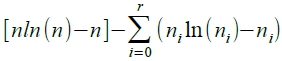

when Ω=Ωₘₐₓ, lnΩ=lnΩₘₐₓ → dlnΩ=0

consraints: 1. fixed V, εᵢ known and fixed. 2. U=Σnᵢεᵢ dU=0 in equilibrium. 3. Total particle number, n=Σnᵢ dn=0

δU=0, δU=Σεᵢδnᵢ=0...(i), δn=Σδnᵢ=0...(ii),

δlnΩ=

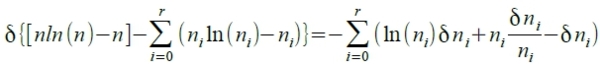
δlnΩ=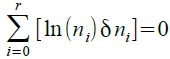  ...(iii)

Q: (i)(ii)(iii)同時成立, nᵢ=?

利用lagrange multiplier method, β(i)+α(ii)+(iii)=0 i.e. α, β均為常數

→

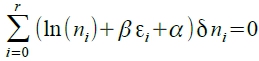
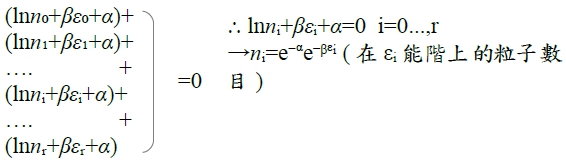
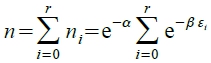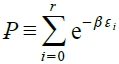 , 令   partition function, → n=e⁻^αꝐ → α=ln(Ꝑ/n), β=?

⸫ nᵢ=(n/Ꝑ)e⁻^βε ͥ when n very large, Ω_mₐₓ≈Ω_tₒ_tₐ_l

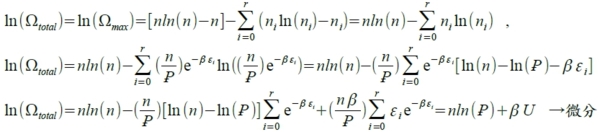
i.e. Σnᵢ=Σ(n/Ꝑ)e⁻^βε ͥ , U=Σnᵢεᵢ=Σεᵢ(n/Ꝑ)e⁻^βε ͥ

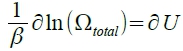  vs. TdS=dUᵥ

統計熱力與古典熱力的式子比較之下, Boltzmann給熵一個統計熱力的定義式:S≡kln(Ω_tₒ_tₐ_l)

S≡kln(Ω_tₒ_tₐ_l) → dS=kdln(Ω_tₒ_tₐ_l), dUᵥ=TdS=kTdlnΩ vs. ∂U=(1/β)∂lnΩ,

⸫ β=(1/kT) → ln(Ω_tₒ_tₐ_l)=nln(Ꝑ)+U/kT

and α=ln(Ꝑ/n) i.e. 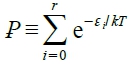   , nᵢ/n=(e⁻^ε ͥ ^/kT)/Ꝑ k∙n_ᴀ=R 氣體常數

小結: 2^nd law: dSᵤ_,ᵥ≥0, when equilibrium, Sᵤ_,ᵥ=Sₘₐₓ. S即表示亂度(randomness, mixed-up-ness)

Boltzmann定義 S≡kln(Ω_tₒ_tₐ_l)

考慮一個系統,體積固定(dV=0)表示能階固定(ε₀, ε₁, ε₂, …,εᵢ),含有n個粒子,有固定的內能(dU=0),當平衡時,

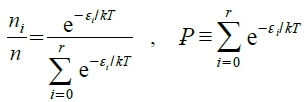
Heat flow: 兩密閉系統A, B(Tᴀ>Tᴃ), 當A,B接觸最後溫度相等( Tᴀ=T=Tᴃ)

Ω=Ωₘₐₓ as equilibrium, it means _A×_Bmax. 熱流停止, 表示δln_A_B=0=δq/kT=dUᵥ/kT

對A: 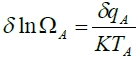 , 對B: 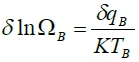 ∵δq_A=-δq_B=δq<0 Heat flux

A+B合併: 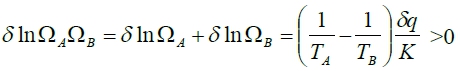 (過程中)

當T_A=T_B時, _A×_Bmax. 平衡

Thermal entropy, Sₜₕ: 溫度改變造成entropy改變,因為粒子在能階上重新分布!!

configuration entropy, S_ᶜₒₙ_ᶠ: 空間上排列重新分布

e.g. 4A4B填8個位置, 總共有70種排列方式(C⁸₄), 其中最可能的排列分布狀態(C⁴₂C⁴₂=36)

Ex. entropy of mixing, S_mᵢₓ

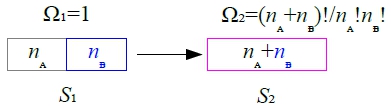
∆S=S₂-S₁=klnΩ₂-klnΩ₁=kln(Ω₂/Ω₁)=kln[(n_ᴀ+n_ᴃ)!/n_ᴀ!n_ᴃ!]

Sₜₒₜₐₗ=Sₜₕ+S_ᶜₒₙ_ᶠ=klnΩₜₕ+klnΩ_ᶜₒₙ_ᶠ=kln(Ωₜₕ∙Ω_ᶜₒₙ_ᶠ)

若原子不同時, 不但有熱熵還有配列熵(混合位置可分辨數目), 事實上兩件事(熱流和擴散)同時發生; 擴散時原子鍵結能改變(ε_ᴀ₋ᴀ≠ε_ᴀ₋ᴃ)產生熱,造成clustering or oedering.

補充: DeHoff ch. 6 已知能階εᵢ, 可得Ꝑ =Σe⁻^ε ͥ ^/kT, 再從Ꝑ計算S, A, U, cᵥ

前面推導中, 因為lnΩ=nln(Ꝑ)+U/kT → kTlnΩ=nkTln(Ꝑ)+U

S≡klnΩ=nkln(Ꝑ)+U/T, 利用Helmholtz free energy, A=U-TS=U-T(nkln(Ꝑ)+U/T)=-nkTln(Ꝑ)

dA=-SdT-PdV ⸫S=-(∂A/∂T)ᵥ=nkln(Ꝑ)+nkT[∂ln(Ꝑ)/∂T]ᵥ

U=A+TS=-nkTln(Ꝑ)+T{nkln(Ꝑ)+nkT[∂ln(Ꝑ)/∂T]ᵥ}=nkT²[∂ln(Ꝑ)/∂T]ᵥ

cᵥ=(δQ/dT)ᵥ=(∂U/∂T)ᵥ

Ex. 1 mole atoms, and 2 energy levels: ε₁=ε, ε₂=2ε; 求S, A, U, cᵥ

Sol: Ꝑ=e⁻^ε/kT+e⁻²^ε/kT=e⁻^ε/kT(1+e⁻^ε/kT) → lnꝐ=-(ε/kT)+ln(1+e⁻^ε/kT)

n₁/n=e⁻^ε/kT/Ꝑ=1/(1+e⁻^ε/kT), n₂/n=e⁻²^ε/kT/Ꝑ=1/(e^ε/kT+1)

*hint: 1. T→0, e⁻^ε/kT→0 ⸫n₁/n_ᴀ→1 whereas e^ε/kT→∞ ⸫n₂/n_ᴀ→0

2. T→∞, e⁻^ε/kT→1 ⸫n₁/n_ᴀ→½ whereas e^ε/kT→1 ⸫n₂/n_ᴀ→½

U=n_ᴀkT²[∂ln(Ꝑ)/∂T]ᵥ=n_ᴀkT²{∂[-(ε/kT)+ln(1+e⁻^ε/kT)]/∂T}ᵥ= n_ᴀkT²[(ε/kT²)+(ε/kT²)(n₂/n_ᴀ)]=n_ᴀε+n₂ε

= n_ᴀε[1+1/(e^ε/kT+1)]

A=-n_ᴀkTln(Ꝑ)=n_ᴀkT[(ε/kT)-ln(1+e⁻^ε/kT)]= n_ᴀε-n_ᴀkT ln(1+e⁻^ε/kT)

Ex. 鉛同位素isotopes的占比, 求S_ᶜₒₘₚ?

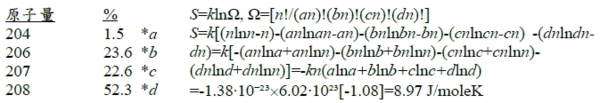
Ex. 氮氣分子光譜有4條,問T=? 是否平衡?

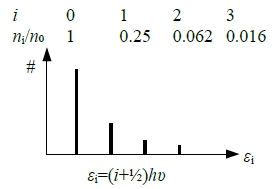
Sol: ⸪ nᵢ/n=(e⁻^ε ͥ ^/kT)/Ꝑ i.e.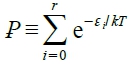

n₁/n₀=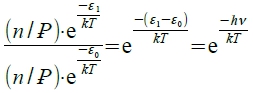 → 0.25=e⁻^ℎν/kT T=2420K

If equil. n₀Ꝑ /n= e⁻^ε₀/kT=e⁻^ℎν/²kT =0.5

n₁Ꝑ /n= e⁻^ε₁/kT=e⁻³^ℎν/²kT =0.125, n₁/n₀=0.25

n₂Ꝑ /n= e⁻^ε₂/kT=e⁻⁵^ℎν/²kT =0.031, n₂/n₀=0.062

n₃Ꝑ /n= e⁻^ε₃/kT=e⁻⁷^ℎν/²kT =0.008, n₃/n₀=0.016 match with experiment, equilibrium!

Gaskell ch. 6-1~6-2. DeHoff ch. 6

內能U, 可推得cᵥ≡(∂U∕∂T)ᵥ=(δQ/dT)ᵥ or δQᵥ=dUᵥ=cᵥdT

If cᵥ(T) known, ∆Q=∫cᵥdT cᵥ(T)=? 也可由cₚ=cᵥ+(TVα²/β) 去求 cᵥ

同理, if cₚ(T) known, ∆Q=∫cₚdT i.e. δQₚ=dHₚ=cₚdT

Given εᵢ, 可推得nᵢ. U=Σnᵢεᵢ=?

◎金屬或共價晶體的內能和cᵥ: 金屬晶格內金屬鍵做震盪,能量存在鍵結中,加總起來成為內能Einstein的假設與模型,以Simple Cubic為例,有N個原子,3維中每個原子有3個自由度可以共振,所以有3N個鍵結.

假設 ε_i=(i+½)hv, i=0,1,2,3... 頻率v固定

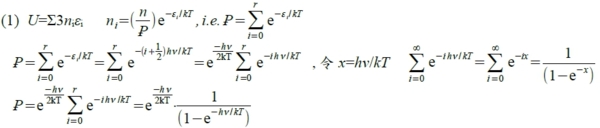
(2) U=3NkT²[∂ln(Ꝑ)/∂T]ᵥ

用上式₽取ln, ln₽=-ℎν/2kT-ln(1-e⁻^ℎν/kT) → U=3NkT²[∂ln(Ꝑ)/∂T]ᵥ

= 3NkT²[ℎν/2kT²-(ℎν/kT²∙-e⁻^ℎν/kT)/(1-e⁻^ℎν/kT)]=3Nℎν/2+3Nℎν[(e⁻^ℎν/kT)/(1-e⁻^ℎν/kT)]=3Nℎν/2+3Nℎν[1/(e^ℎν/kT-1)]

→ cᵥ≡(∂U∕∂T)ᵥ=3Nℎν[(ℎν/kT²)∙e^ℎν/kT/(e^ℎν/kT-1)²]=3Nk(ℎν/kT)²[e^ℎν/kT/(e^ℎν/kT-1)²]

定義Einstein temp. θᴇ≡ℎν/k, cᵥ=3Nk(θᴇ/T)²[e^θᴇ/T/(e^θᴇ/T-1)²]

結果與實驗比較, cᵥ→3R as T→high temp. and cᵥ→0 as T→0, 中間的誤差起因於假設固定頻率,實際上共振的頻率互相有關,分布在一個範圍

T³ law: θᴆ/T→∞ at low T, 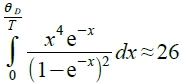  , cᵥ~T³

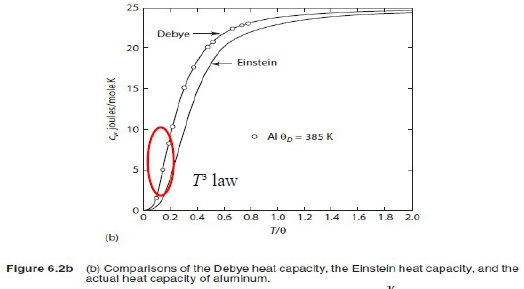
Debye針對頻率做修正,提出『頻譜』g(ν)=(9n/νₘ³) ν² and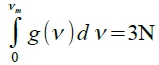  

定義Debye temp. θᴆ≡ℎνₘ/k, 

  

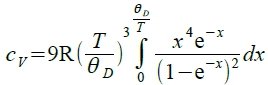
, x=ℎν/kT well fitting with experiment.

計算太複雜! 改由量測cₚ(T)=? 從cₚ=cᵥ+(TVα²/β) 去求 cᵥ? cₚ(T)=a+bT+cT⁻² a,b,c查表

金屬的自由電子對heat capacity的貢獻?

Compound, AₘBₙ: cₚ(AₘBₙ)≈mcₚ_(A)+ncₚ_(B) Kopps rule

Kopp: 化合物的heat capacity=元素(組成)heat capacity之和

補充: 理想氣體的內能(U)和熱容量(cᵥ)

將U看成所有原(分)子的動能(K.E.),

1. 單原子 K.E.=½∙mvᵢ²=Eₖ

假設一單原子以速度v在(lₓ,l_y,l_z)的空間中運動, 0<position(x,y,z)<(lₓ,l_y,l_z) and -∞<(vₓ,v_y,v_z)<∞

Eₖ= ½∙mv²= ½∙m(vₓ² +v_y² +v_z ²) → Ꝑ=Σ e⁻^εᵢ/kT, εᵢ=½∙m(vₓᵢ² +v_yᵢ² +v_zᵢ ²)

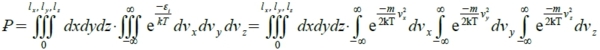
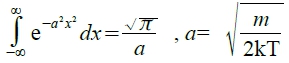 ⸫ ₽=V∙(2πkT/m)^½(2πkT/m)^½(2πkT/m)^½=V∙(2πkT/m)^3/2

→ lnꝐ=lnV+(3/2)ln(2kπ/m)+(3/2)lnT ⸪ U=nkT²[∂ln(Ꝑ)/∂T]ᵥ=nkT²(3/2)(1/T)=3nkT/2

If n=Nᴀ, Nᴀ∙k=R ⸫ U=3nkT/2=3RT/2 → cᵥ=(∂U∕∂T)ᵥ=3R/2

證明 Nᴀ∙k=R

dA=-SdT-PdV → P=-(∂A∕∂V)_ᴛ and A=-nkTln(Ꝑ) → P=nkT[∂ln(Ꝑ)∕∂V]_ᴛ

lnꝐ=lnV+(3/2)ln(2kπ/m)+(3/2)lnT → P=nkT(1/V) 比較 PV=RT if n= Nᴀ ⸫ Nᴀ∙k=R

ex. D=D₀e⁻^ε/kT(單一粒子)=D₀e⁻ᴱ^/RT(1 mole粒子) Arrehnius eq.

2. diatomic, polyatomic case, U=?

例如: 雙原子除了移動以外,振動和轉動

*3 translation: ½∙m(vₓ² +v_y² +v_z ²), *1 vibration: ½∙mω²(A²-x²)~bᵥυᵥ² *1 rotation ½∙Iω²~bᵣυᵣ²

→ εᵢ=Σb_ʲυ_ʲ² j=1, 2,..., n

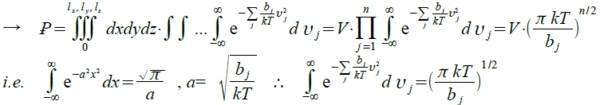
→ lnꝐ=lnV+(n/2)ln(kπ/b_ʲ)+(n/2)lnT

→ U=NᴀkT²[∂ln(Ꝑ)/∂T]ᵥ=NᴀkT²(n/2)(1/T)=NᴀkT(n/2)=RT(n/2)

"Priciple of equipartition of energy"能量等分原理: each indep. Component of motion contributes to U by ½∙kT(½∙RT)

⸫ Diatomic n=5(3t+1r+1v) → U=5RT/2, cᵥ=5R/2 e.g. N₂, O₂, H₂(假設為理想氣體)

實際上, N₂(N≡N) 因為strong bond彈性係數高,振動小→ Eᵥ<Eᵣ<Eₜ cᵥ<5R/2

Ex. NH₃