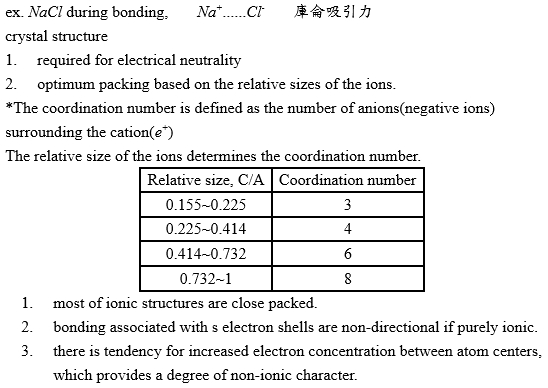
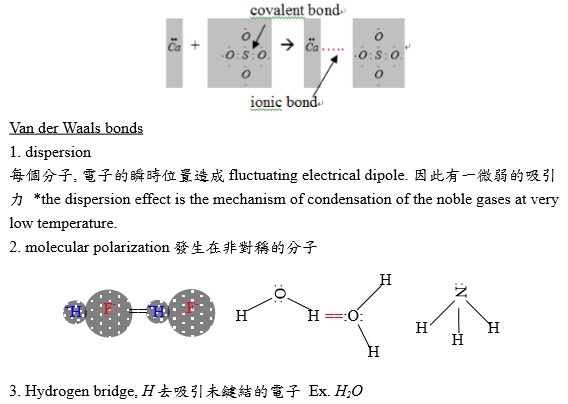
金屬物理第一章 純金屬的結構
§電子結構和週期表
元素的物性和化性有關於原子的電子結構,先從自由原子談起,自由原子包括帶正電的原子核加上包圍的電子雲;原子序Z等於原子的電子數,也等於質子數
一些常數特性: 電子電荷|-e|=1.610⁻¹⁹coul, mₑ=9.1110⁻³¹Kg, r原子核=10⁻¹³cm, r原子=10⁻⁸cm,
mₚ=1836mₑ, mₙ=1839mₑ, 質量數=質子數+中子數
同位素: Z相同,但原子量不同的元素原子, ex. U²³⁵和U²³⁸, U有92個質子,但分別有143和146個中子
原子量以C¹²為準,自然界存在的同位素,其混合物依照混合比例,加權平均級可得平均原子量
量子理論: 電子態由四個量子數(n, l, mₗ, mₛ)確定每一個電子的能態
主量子數, n=1, 2, 3,...軌道層次orbital shell(縮寫K, L, M,..., Q)
角動量, l=0, 1, …, n-1 次軌道subshell縮寫 s, p, d, f, …
磁角動量, mₗ=-l, …, -1, 0, 1, …, l 次軌道數 Nₛ=1, Nₚ=3, Nᵈ=5, Nᶠ=7
自旋量子數, mₛ=±½ 每一軌道可容納自旋相反的2個電子
Pauli不相容原理: 每一種能態只能容納一個電子
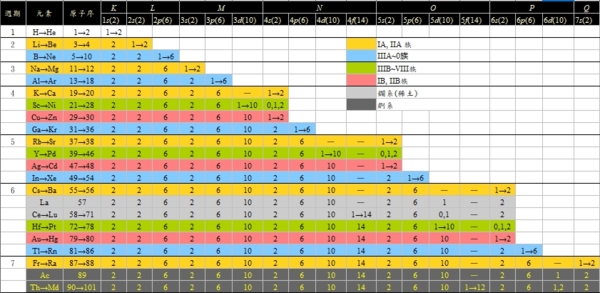
對多電子原子而言,能階的高低必須同時考慮主量子數(n)及角量子數(l),由(n+l)的大小來決定能階的高低
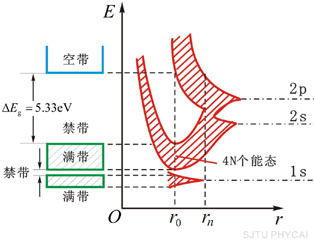
多數實用的金屬材料都和過渡族元素(IIIB~VIII族)有關,也就是從第四周期開始出現d軌道的緣故: IA和IIA的K和Ca,其外層的價電子填入N shell的4s軌道, 隨後的元素鈧Sc到鎳Ni, 外層電子優先填入M shell的3d軌道,之後的銅Cu和鋅Zn的外層電子才進入3d外面的4s軌道; 雖然銅Cu和鋅Zn具有和K與Ca相同的外層價電子,但是由於存在的3d填滿軌道,其物性與IA和IIA族金屬很不一樣,所以分別歸於IB和IIB族
依照上述, 3d和4s的能量差很小; 在K原子中E₄ₛ₃ᵈ, 在Cu原子中E₄ₛ>E₃ᵈ; 這種3d到4s相對能量的變化(能級交錯*),從鈧Sc到鎳Ni逐漸過渡,所以這些元素稱為過渡族元素(IIIB~VIII族), 在填充3d軌道的過程中, 4s軌道的電子可以是0, 1或2, 使過渡金屬具有可變的價電子數
ns和(n-1)d的能級接近是和過渡族金屬的許多特性有關,類似的情形在第五、第六周期也有,像E₄ᵈ逐漸小於E₅ₛ, 6s/5d/4f的能量非常接近
*能級交錯: 同一電子層之間有電子的相互作用,不同電子層之間也有相互作用,這種相互作用稱為鑽穿效應。其原理較為複雜,鑽穿效應的直接結果就是上一電子層的d能級的能量高於下一電子層s的能量。即,d層和s層發生交錯,f層與d層和s層都會發生交錯。
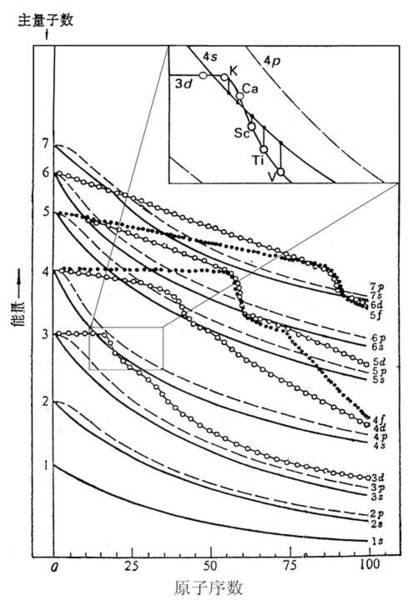
金屬電子理論
光學現象中有波粒二象性,電子也有類似的特性,先從宏觀的振動和波入手,ex. 彈簧加載振動
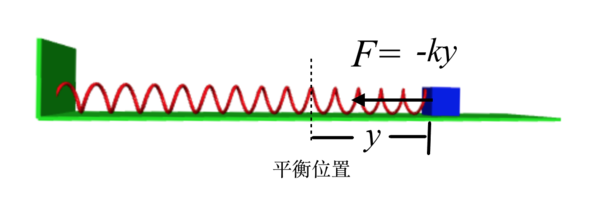
⸪k/m=(2πν)² ν: 振動頻率 ⸫ d²y/dt²+(2πν)²y=0...(1) y=Acos2πνt
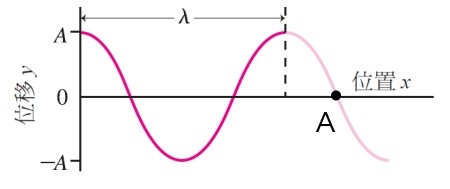
⸪υ=νλ ⸫y(x,t)=Acos2π(νt-x/λ)...(2) 一維平面波函數
為簡化運算,可寫成複數形式 y(x,t)=Aei2π(νt-x/λ)...(3) 所以(2)和(3)是等效的
⸪eiθ=cosθ+isinθ ⸫ y(x,t)=A[cos2π(νt-x/λ)+isin2π(νt-x/λ)]...(4)
對(3)求x, t的二次導數
∂²y/∂t²=-(2πν)²y, ∂²y/∂x²=-(2π/λ)²y 代入 υ=νλ
即可得波動方程式 (1/υ²)∂²y/∂t²=∂²y/∂x²...(5)
平面波函數的複數形式, 可使x, t自變數分離, 把(3)分成ei2πνt和ψ(x)=Ae-i2πx/λ的乘積, 前者是時間的函數,後者是波動的空間分布, 它們的共軛複數也能滿足方程式,也是特殊解
自由電子的波函數(表示無未能障礙, V=0), 我們將(3)寫成 y(x,t)=ψ(x)ei2πνt , ψ(x)=Ae-i2πx/λ
代入(5)消去ei2πνt, 可得 d²ψ/dx²+(4π²ν²/υ²)ψ=0 → d²ψ/dx²+(2π/λ)²ψ=0...(6)
(6)是波長為λ的電子波動方程式,由於去掉時間變數,稱為定態(不隨時變)波動方程式
有了自由電子的波函數, 就可以確定在晶體中某處找到電子的機率
使ψ(x)=Ae-i2πx/λ=Ae-iθ , θ=2πx/λ → ψψ*=A²e-iθeiθ=A² 對一維晶體, ψψ*是在座標為x及x+dx區間中找到電子的機率, 其值是波的振幅的平方A²
在晶體中找到自由電子的總機率 ∫ᴸ₀ψψ*dx=A²L, L是一維晶體的長度
為使總機率為1比較方便, 波函數需要歸一化, 使∫ᴸ₀ψψ*dx=1 即 A²L=1, A=1/√L
歸一化波函數 ψ=(1/√L)e-iθ...(7)
在晶體中某處找到電子的機率 ψψ*=(1/L)e-iθeiθ= 1/L=常數, 表示找到電子的機率處處相等;當V=0時,電子在金屬中的分布是均勻的
最後由邊界條件找出允許波長, 設想把一維晶體彎成一個金屬環,其周長為L, 則x和x+L處的電子波函數應該相等: ψ(x)=ψ(x+L) Born-Karman 邊界條件
(7)的實部: ψ(x)=(1/√L)cos2πx/λ
ψ(x+L)=(1/√L)cos2π/λ(x+L)=(1/√L)[(cos2πx/λ)(cos2πL/λ)-(sin2πx/λ)(sin2πL/λ)]
要滿足條件,必須 cos2πL/λ=1 和 sin2πL/λ=0
→ 2πL/λ=±2πn ...(8) ⸫ λ=L/n, n=±1, ±2, ±3, …, ±N/2(N為金屬環中的原子數)
結論: N個原子組成的晶體,簡併能級發生分裂,分裂成N個允許波長,這些波長不能連續變化,只允許取分立的值,1/λ 是1/L的整數倍, n可以取±1, ±2, ±3, …, ±N/2值,最大的波長是L; 最小的波長是2L/N=2Na/N=2a, a是原子間距
晶體點陣中的允許能級
電子具有粒子和波動二象性,粒子的動能E和動量P, 與波動的頻率ν和波長λ,之間的關係:
E=hν, P=h/λ h=6.62610⁻³⁴m²Kg/s
古典力學中, E=½mv², P=mv v是速度 λ=h/mv ⸫ E=h²/2mλ² ...(9)
將 λ=L/n代入(9), E=n²h²/2mL² ...(10) n=±1, ±2, ±3, …, ±N/2
自由電子的本徵函數和能量本徵值
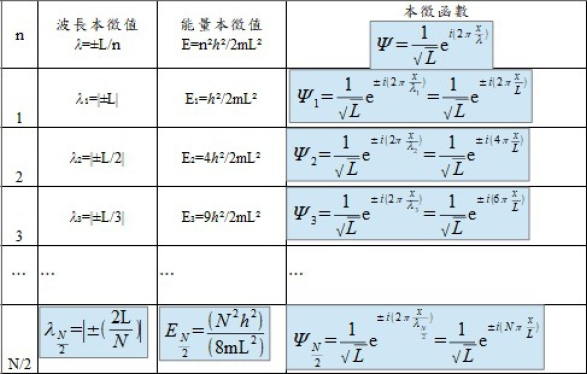
這些分立的能級構成能帶,在晶體中N的數目很大,相鄰能級間的波長差和能量差很小,形成一個“準連續”的能譜, 每個能級可以容納2個自旋反平行的電子
K空間和能態密度
將一維晶體推廣到三維晶體: λ=L/n, ϵ=n²h²/2mL² ...(10) n=±1, ±2, ±3, …, ±N/2
ϵ=(nₓ²+nʸ²+nᶻ²)h²/2mL² nₓ=±1, ±2, ±3, … nʸ=±1, ±2, ±3, … nᶻ=±1, ±2, ±3, …
ϵ=n²h²/2mL²=(nₓ²+nʸ²+nᶻ²)h²/2mL²=, n²=(nₓ²+nʸ²+nᶻ²)½
令Kᵢ=1/λᵢ=nᵢ/L, ⸫ ϵ=(Kₓ²+Kʸ²+Kᶻ²)h²/2m= h²K²/2m...(11) Kₓ=±1/L, ±2/L, ±3/L, … Kʸ=±1/L, ±2/L, ±3/L, … Kᶻ=±±1/L, ±2/L, ±3/L, …
n轉換至K空間(單位長度=1/L), 所以每個能階代表點的體積佔據(1/L)³=1/V, 亦即單位體積內包含V個能階數,設想K空間為一球座標, 0點為球心,同一半徑上的球面,能量均相等但方向不同, 能階數dZ=4πK²dK∙V, 可容納電子數(能態數)dZ=2(4πK²dK∙V)=8πK²dK∙V...(12)
(11)式對K微分, dϵ=2h²KdK/2m=h²KdK/m 代入(12)
dZ=8πK(mdϵ/h²)∙V=8πVmdϵ/h²(2mϵ/h²)½=4πV(2m/h²)3/2ϵ½ dϵ
Define 能態密度N(ϵ)=dZ/dϵ=4πV(2m/h²)3/2ϵ½ N(ϵ) vs. ϵ為一拋物線
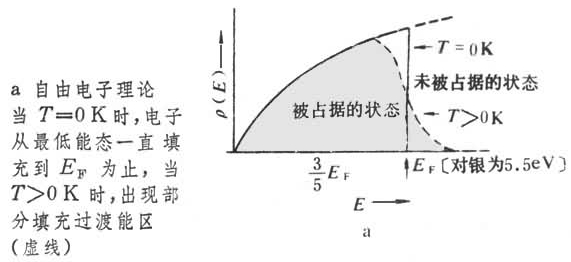
在T=0 K時, 分布機率 f =1/(e⁽ᴱ⁻ᴱᶠ⁾/ᵏᵀ+1) EF為T K時的費米能階
當T=0 K, (I)若ϵ>EF則f=0, (II) 若ϵF則f=1
當T>0 K, (I)若ϵ=EF則f=1/2, (II) 若ϵ-EF=kT則f=1/(e+1)=0.27
kT≈1/40 eV, EF=4 eV 所以kT≈0.01 EF 表示只有接近EF 的電子能夠吸收能量,跳升到高能階,亦即只有一小撮墊子能夠吸收熱能,對比熱的貢獻可以忽略
由能態密度N(ϵ)和分布機率可以算得 EF⁰
電子數 dN/dϵ=f∙N(ϵ)=C∙f∙ϵ½ C=4πV(2m/h²)3/2
(I)當T=0 K,若ϵF則f=1 ⸫ 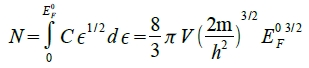 (13)令 n=N/V 電子濃度
(13)令 n=N/V 電子濃度
→ 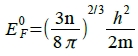 ex. 單價金屬EF⁰, Li(4.7), Na(3.2), K(2.1), Ag(5.5)
ex. 單價金屬EF⁰, Li(4.7), Na(3.2), K(2.1), Ag(5.5)
電子的平均能量 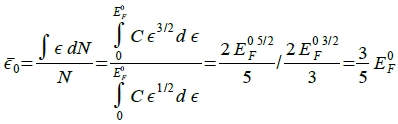
(II)當T>0 K, 若ϵ-EF=kT and kT<< EF
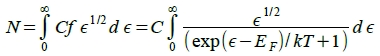 =常數, ⸫ dN/dT=
=常數, ⸫ dN/dT= 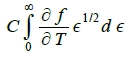 =0
=0
由(13)得N=8πV/3(2m/h²)3/2ϵ3/2
取對數→ lnN=1.5lnϵ+C →微分 dN/N=1.5(dϵ/ϵ), N(ϵ)=dN/dϵ=1.5(N/ϵ)
自由電子總能: 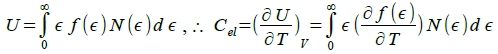
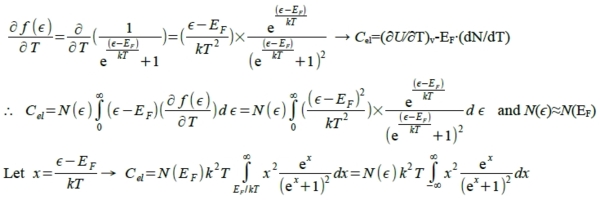
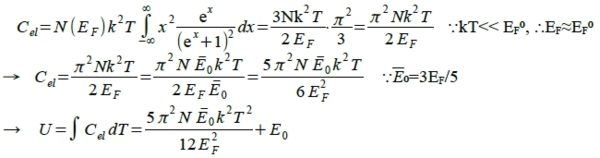
比熱的計算 (推導)