Chap. 1 crystal structure

Crystal structure: an ideal crystal is constructed by an infinite repeatition in space of identical structure units.

Lattice—點之間的關係

r=r+u₁a₁+u₂a₂+u₃a₃… (a) u₁,u₂,u₃ are integrals

Crystal lattice={lattice point}={r|r=r+u₁a₁+u₂a₂+u₃a₃}

1. primitive axes—a₁, a₂, a₃ primitive translational vector, any two points 之間rr滿足(a).

2. Primitive cell—the parallepiped defined by primitive axesa₁, a₂, a₃ is called a primitive cell. 只有一個lattice point, V_c=|a₁∙a₂a₃|若是primitive cell, 體積是最小的

Another way of choosing a primitive cell: Wigner-Seitz cell

Basis—atom array in a cell

crystal structure=lattice+basis, r_j=x_ja₁+y_ja₂+z_ja₃ x_j≤1, y_j≤1, z_j≤1在cell內部

Fundamental types of lattices

Symmetry operators—the symmetry operators of a crystal carry the crystal structure into itself.

1. lattice translation T=u₁a₁+u₂a₂+u₃a₃

2. mirror reflection

3. inversion: r→-r

4. rotation

角度限制	60	90	120	180	360
對稱性	6 fold	4	3	2	1

,2的旋轉,任何lattice均不變

Bravais lattice: 5 2-D and 14 3-D

2-D lattice 用a₁,a₂, 表示

i) oblique: a₁a₂, 90, ii) square: a₁=a₂, =90 iii) hexagonal: a₁=a₂, =120 iv) rectangular: a₁a₂, =90, v) centered rectangular: a₁a₂, =90

3-D lattice用a₁,a₂,a₃,,, 表示7 systen/14 types

1. one fold 對稱, Triclinic a₁a₂a₃,  P(1)

2. Monoclinic a₁a₂a₃, ==90 P, C(2)

3. Orthorhombic a₁a₂a₃, ===90 P, C, I, F(4)

4. Tetragonal a₁=a₂a₃, ===90 P, I(2)

5. Cubic a₁=a₂=a₃, ===90 P, I, F(3)

6. Trigonal a₁=a₂=a₃, ==<12090 P(1)

7. Hexagonal a₁a₂a₃, ==90, =120 P(1)

Cubic lattice

1. S.C.(Simple cubic)

2. B.C.C.(Body centered cubic)

3. F.C.C.(Face centered cubic)

Number of nearest neighbors and its distance

(i)S.C.: (6, a) (ii)B.C.C.: (8, √3a/2 ) (iii)F.C.C.: (12, √2a/2 )

Volume of primitive cell

1. S.C.: a³

2. B.C.C.: a₁=½a(i+j-k), a₂=½a(-i+j+k), a₃=½a(i-j+k)

Vₚ=|a₁∙a₂a₃|=(a/2)³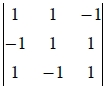 = a³/2

1. F.C.C.: a₁=½a(i+j), a₂=½a(j+k), a₃=½a(i+k) Vₚ=|a₁∙a₂a₃|=(a/2)³  =a³/2

Packing fraction(p.f.): the maximum proportion of the available volume that an be filled with hard spheres.

1. S.C.: volume of a sphere=4π/3(a/2)³, number of hard sphere in a cubic cell=1, volume of cell=a³. p.f.= [4π/3(a/2)³]/a³=π/6=0.524=52.4%

2. B.C.C.: volume of a sphere=4π/3(√3a/4)³ , number of hard sphere in a cubic cell=2, volume of cell=a³. p.f.= 2[4π/3(√3a/4)³]/a³=√3π/8=0.68=68%

Miller indices:   1/X₁:1/X₂:1/X₃=h:k:lplane’s indices=(h,k,l)

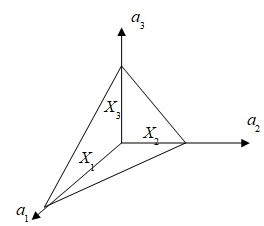
direction: [u,v,w]=ua₁+va₂+wa₃

* only in cubic system, [h,k,l](h,k,l)

{1,0,0} includes (1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1), (0,0,-1)

Simple crystal structure

1. NaCl structure: crystal structure=lattice + basis, space lattice: F.C.C. and basis: two atoms. Cl^- :(0,0,0), Na⁺:(½, ½, ½)

2. CsCl structure: space lattice: S.C. and basis: two atoms. Cs⁺:(0,0,0), Cl^-:(½, ½, ½)

3. hexagonal close-paced structure has maximum packing factor.

4. Diamond: space lattice: F.C.C.(兩個F.C.C.交錯) and basis: two atoms. (0,0,0), (¼,¼,¼), 4 neighbor atoms.

In cubic system, the direction[h,k,l] is perpendicular to (h,k,l)

A=ha₁+ka₂+la₃, AB=0B-0A=a₂/k-a₃/h, AC=0C-0A=a₃/l-a₁/h,

N=ACAB=(1/hkl)[la₁a₂+ka₃a₁+ha₂a₃]

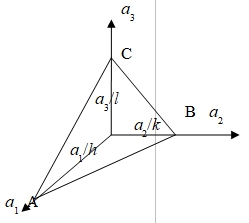
欲[h,k,l]plane(h,k,l) → N // A

m(a₂a₃)=a₁, n(a₃a₁)=a₂, p(a₁a₂)=a₃

a₁∙a₂=0, a₁∙a₃=0 ⸫ a₁, a₂, a₃ is orthorgonal.

a₁=m(a₂a₃)=m(a₂a₃/a₁)a₁ → m=a₁/a₂a₃, n=a₂/a₁a₃, p=a₃/a₁a₂ N=nA, nR N=(1/hkl)[l(a₁a₂/a₃)a₃+k(a₁a₃/a₂)a₂+h(a₂a₃/a₁)a₁] → h:k:l=h(a₂a₃/a₁):k(a₁a₃/a₂):l(a₁a₂/a₃)

tell us a₂a₃/a₁=a₁a₃/a₂=a₁a₂/a₃ → a₁=a₂=a₃

所以cubic system a₁=a₂=a₃, ===90, [h,k,l](h,k,l)