小學生的數學競賽延伸題
2007/12/09 13:09
瀏覽2,227
迴響7
推薦38
引用0
迴響（7） ：
7樓. ken2013/09/08 11:464樓. 都都
可說說S(1)為何?
-
6樓. 都都2007/12/13 19:08下面的題目有打錯
第2題應該是10^n,因為沒辦法顯示上標所以錯誤了.sorry真是抱歉，最近幾天聊到把這事忘了
.....我現在抽個空，來解解看．
梅斯普雷爾 於 2007/12/14 11:09回覆 
5樓. 鳳彩翎：阿9公然侮辱2007/12/12 17:45有沒有...
令人比較有溫馨感覺的數學?
您覺得背一次９９乘法的提議如何？回味一下童年！
梅斯普雷爾 於 2007/12/12 22:08回覆
4樓. 都都2007/12/11 19:19幫我看一下...
因為不知道為什麼知識+一直不給我發問(說內容不夠清楚= =但是明明就很完整了)
所以只好來跟你求救XD....AIME的歷屆試題
1. 若正整數N<1000且恰可以表示成5種 j 個連續正奇數之和,j ≧1,試問這種N共有多少個 ?
2.由1,2,3,...,10n之所有整數中, 其非0的各位數字倒數和設為Sn,試求使得Sn是整數的最小整數n?
3.某數列定義如下: a1=a2=a3=1,且對於任意的正整數n,an+3=an+2+an+1+an, 已知a28=6090307, a29=11201821, a30=30603361,試求a1+a2+...+a28 除以1000的餘數?謝謝!
你可以把他打成文張貼出來^^當作分享也不錯
3樓. 時和2007/12/10 09:45看懂了
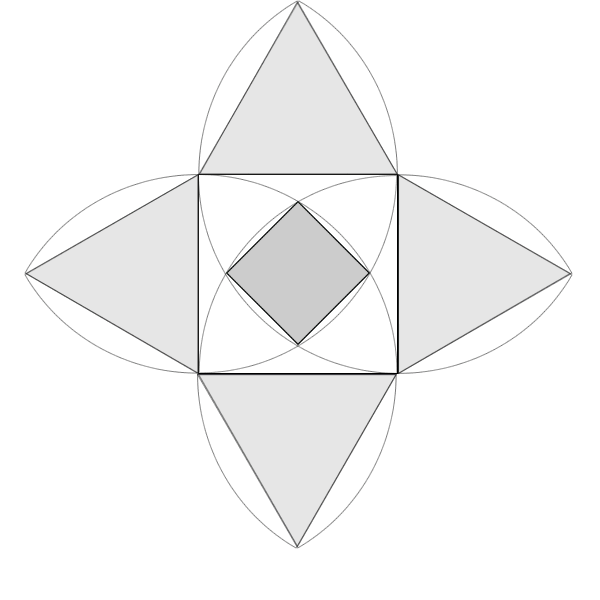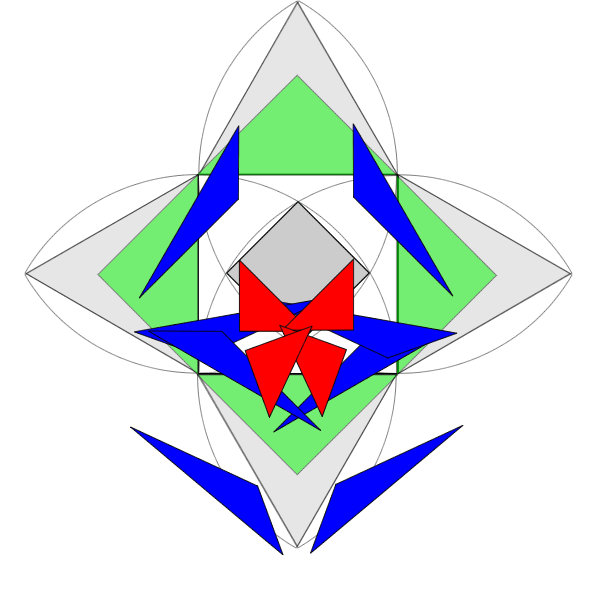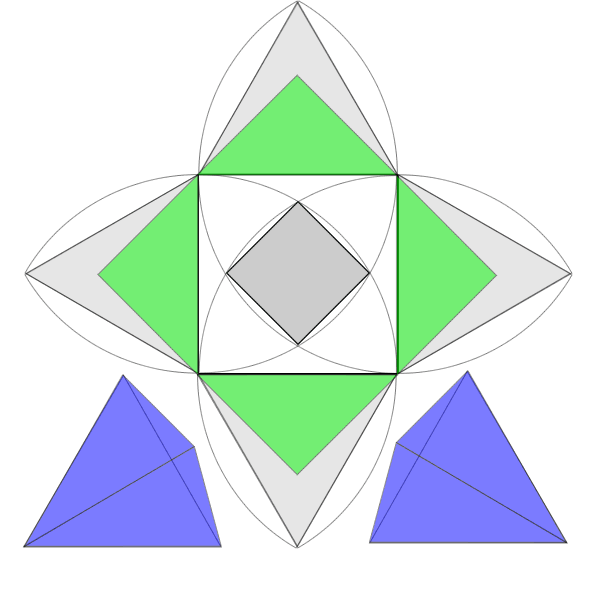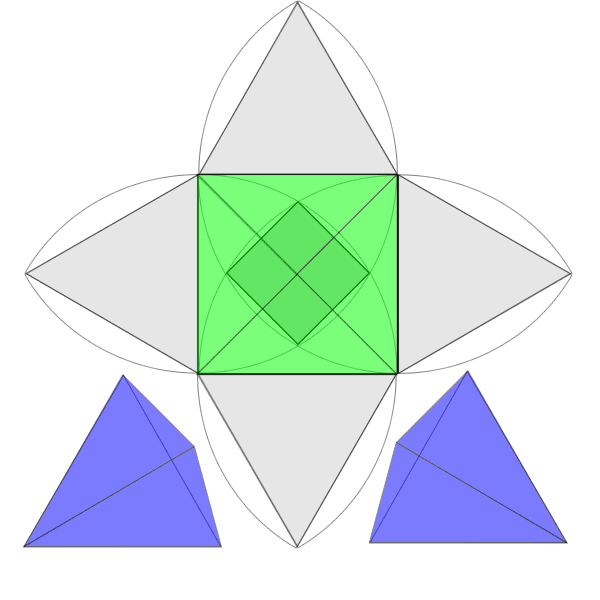
在前一篇「數學狂想筆記：阿基米得上身」的〝圖一〞中的解釋。
因此這題確實可以不用計算核心小正方形的邊長。
用不著計算無理數，果然可以當成小學生的題目。
梅斯大俠確實高竿！
出題的人不是我，我只是剛好遇上這樣的好題目，所以手癢．
梅斯普雷爾 於 2007/12/10 13:05回覆-
2樓. 時和2007/12/10 09:26這個轉換過程雖然是對的
但是得證明！
而在證明的過程中，很可能得先求出核心小正方形的邊長。
感覺上還是直接算來得快？
因為是小學競賽的題目，所以只好作這樣的轉換，以避開無理數的計算．
梅斯普雷爾 於 2007/12/10 13:01回覆
1樓. 醉米粒2007/12/10 00:15圖形看起來
像 mandala....
我不打發日子，日子天天打發我...咦 確實是ㄟ．呵呵． 梅斯普雷爾 於 2007/12/10 00:23回覆
