.
國民愛吃巧克力 諾貝爾得主多
（中央社紐約11日綜合外電報導）有關「黑金」巧克力的研究千奇百怪，但最新發布在世界一流期刊的研究確實前所未聞。這份研究指出，一國巧克力攝取量越高，按人均計算的諾貝爾得主也越多。
根據這份刊登在「新英格蘭醫學期刊」（New England Journal of Medicine）報告，研究主筆梅瑟里（Franz Messerli）的資料分析，瑞士人巧克力攝取量最高，接著是瑞典人與丹麥人，美國則在排行榜中段。而一國必須每年攝取1億2500萬公斤的巧克力，才會誕生1位諾貝爾得主。
紐約聖路加－羅斯福醫院（St. Luke's-RooseveltHospital）高血壓計畫負責人梅瑟里表示：「瑞士民眾，包括男人、女人和小孩，每年平均吃120條重85公克的巧克力棒。這個份量真的很驚人。」
梅瑟里的研究構想，是因為讀到研究指出，可可與葡萄酒中的抗氧化物類黃酮（flavonoids）與認知測驗高成績有關。
他之後開始分析23國巧克力攝取的資料，並與維基百科（Wikipedia）的人均諾貝爾得主國家排名對比。
「我在加德滿都的飯店房間開始分析，因為那時沒事做。結果我不敢相信自己的眼睛。各國在圖表上的排序相當漂亮，也就是巧克力攝取高低與諾貝爾得主人數有關。」
這不是第1次有科學家發現似乎不太合乎邏輯的研究結果。曾有研究指出，歐洲國家送子鳥數量與生育率有關；另有研究顯示男性自殺率和太陽黑子有關。
另一個可能性是，巧克力攝取量與諾貝爾得主數量真的相關，不過這個關聯並無意義。
2001年獲得諾貝爾物理學獎的美國物理學家柯內爾（Eric Cornell）說：「一國巧克力攝取量與國家富裕程度有關；而高品質科學研究也與國家富裕程度相關。」
「因此，以此類推，巧克力攝取量會與高品質研究有關。但中間沒有因果關係。」（譯者：中央社蕭倩芸）1011011
=========================
因果關係
因果關係（Causality），當我們說A與B之間具有因果關係，如果A是因（cause）B是果（effect），則A與B之間必須具備以下四個必要條件（necessary conditions）：
- A與B共變（covary），也就是A增加（或減少）B也增加（或是減少）
- A發生在B之前，也就是「前因」「後果」
- A與B之間的關係具有理論上的連結
- A與B之間的關係不是偽關係（spurious relationship）
- -----------------
- =========
-
格蘭傑因果關係- 维基百科，自由的百科全书
zh.wikipedia.org/zh-tw/格蘭傑因果關係 - 頁庫存檔格蘭傑因果關係檢驗是一種檢驗一組時間序列是否可被用來預測另一組時間序列的假設檢定。迴歸模型通常反襯出變量間的相關性，但諾貝爾經濟學獎得主克萊夫·格 ...
=========
-
-
-
-
-
-
-
-
-
-
-
什麼是相關係數(請查原文！）
相關表和相關圖可反映兩個變數之間的相互關係及其相關方向，但無法確切地表明兩個變數之間相關的程度。著名統計學家
卡爾·皮爾遜設計了統計指標——相關係數。相關係數是用以反映變數之間相關關係密切程度的統計指標。相關係數是按積差方法計算，同樣以兩變數與各自平均值的離差為基礎，通過兩個離差相乘來反映兩變數之間相關程度；著重研究線性的單相關係數。依據相關現象之間的不同特征，其統計指標的名稱有所不同。如將反映兩變數間線性相關關係的統計指標稱為相關係數（相關係數的平方稱為
判定繫數）；將反映兩變數間曲線相關關係的統計指標稱為非線性相關係數、非線性判定繫數；將反映多元線性相關關係的統計指標稱為復相關係數、覆判定繫數等。[編輯]相關係數的幾種定義
相關關係是一種非確定性的關係，相關係數是研究變數之間
線性相關程度的量。由於研究對象的不同，相關係數有如下幾種定義方式。簡單相關係數：又叫相關係數或線性相關係數，一般用字母P 表示，是用來度量變數間的線性關係的量。
復相關係數：又叫多重相關係數。復相關是指
因變數與多個自變數之間的相關關係。例如，某種商品的季節性需求量與其價格水平、職工收入水平等現象之間呈現復相關關係。典型相關係數：是先對原來各組變數進行
主成分分析，得到新的線性關係的綜合指標，再通過綜合指標之間的線性相關係數來研究原各組變數間相關關係。[編輯]
相關係數的性質
[1] (1)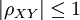
；
(2)定理： | ρXY | = 1的充要條件是，存在常數a，b，使得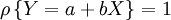
；
相關係數ρXY取值在-1到1之問，ρXY = 0時，
稱X,Y不相關； | ρXY | = 1時，稱X,Y
完全相關，此時，X,Y之間具有線性函數關係； | ρXY | < 1時，X的變動引起Y的部分變動，ρXY的絕對值越大，X的變動引起Y的變動就越大， | ρXY | > 0.8時稱為高度相關，當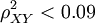
，即 | ρXY | < 0.3時，稱為低度相關，其他為中度相關。
(3)推論：若Y=a+bX，則有
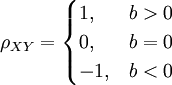
證明： 令E(X) = μ，D(X) = σ2
相關係數的計算方法
相關係數的公式如下: 【例】一種
新產品上市。在上市之前，公司的物流部需把新產品合理分配到全國的10個倉庫，新品上市一個月後，要評估實際分配方案與之前考慮的其他分配方案中，是實際分配方案好還是其中尚未使用的分配方案更好，通過這樣的評估，可以在下一次的新產品上市使用更準確的產品分配方案，以避免由於分配而產生的積壓和斷貨。表1是根據實際數據所列的數表。通過計算，很容易得出這3個分配方案中，B的相關係數是最大的，這樣就評估到B的分配方案比實際分配方案A更好，在下一次的新產品上市分配計劃中，就可以考慮用B這種分配方法來計算實際分配方案。
- 3.在
【例】如果有若幹個
樣品，每個樣品有n個特征，則相關係數可以表示兩個樣品問的相似程度。藉此，可以對樣品的親疏遠近進行距離聚類。例如9個小麥品種(分別用A1,A2,...,A9表示)的6個性狀資料見表2，作相關係數計算並檢驗。由相關係數計算公式可計算出6個性狀間的相關係數，分析及檢驗結果見表3。由表3可以看出，冬季分櫱與每穗粒數之間呈現負相關(ρ = − 0.8982)，即麥冬季分櫱越多，那麼每穗的小麥粒數越少，其他性狀之間的關係不顯著。
相關係數的缺點
需要指出的是，相關係數有一個明顯的缺點，即它接近於1的程度與數據組數n相關，這容易給人一種假象。因為，當n較小時，相關係數的波動較大，對有些樣本相關係數的絕對值易接近於1；當n較大時，相關係數的絕對值容易偏小。特別是當n=2時，相關係數的絕對值總為1。因此在
樣本容量n較小時，我們僅憑相關係數較大就判定變數x與y之間有密切的線性關係是不妥當的。例如，就我國深滬兩股市資產負債率與
每股收益之間的相關關係做研究。發現1999年資產負債率前40名的上市公司，二者的相關係數為r=–0.6139；資產負債率後20名的上市公司，二者的相關係數r=0.1072；而對於滬、深全部上市公司（基金除外）結果卻是，r滬=–0.5509，r深=–0.4361，根據三級劃分方法，兩變數為顯著性相關。這也說明僅憑r的計算值大小判斷相關程度有一定的缺陷。
