分三個部分來談
(一)5,9。同餘數。
(二)倒著背。因式分解。
(三)偶數與奇數。機率。
如果前面兩個很熟悉的話,可以直接從第三部分開始看,這部份是我想寫這篇文的主要原因。
本立而道生,就讓我們先來看一下九九乘法表吧!

(一)5,9。同餘數。
看著九九乘法表,我們會發現5的乘法表很有意思,個位數不是5就是0。
為什麼會如此呢?是因為我們用的是十進位法。10=5X2
5X1=5
5X2=10
5X3=5X(2+1)=10+5
5X4=5X(2+2)=10+10
5x5=5x(2+2+1)=10+10+5
所以5的乘法表的個位數就會是5或0。
10=5x2
所以2的乘法表也有類似的情況,2的乘法表的個位數都會是2的倍數,2,4,6,8,0。
同樣的4也有類似的情況,不過由於4=2x2,所以運用的是100=4x25=2x5x2x5,所以4的倍數的十位數和個位數會是4的倍數。就像10,30,70都會是2的倍數一樣,100,300,700,2300也都會是4的倍數。8的話,就是1000=8x125=2x5x2x5x2x5
現在讓我們看一下9的乘法表。

9x1我們寫成9x1=09
就會發現十位數的變化是從0到8,個位數的變化是從9到1。有點意思,有某種規律的感覺。我們再仔細想點,十位數加個位數的和竟然都會是9。
9x1=09,0+9=9
9x2=18,1+8=9
9x3=27,2+7=9
9x4=36,3+6=9
很神奇!國中時老師教我們用數字相加的和來判斷數字是不是9的倍數。可是知其然而不知其所以然。其實還是跟前面說的原因相同,因為我們用的是十進位法。
10除以9會餘1,100除以9也是餘1,1000,100000,10000000也是餘1。這就是同餘的概念,因為10除以9會餘1,100=10X10=1X1,1000=10X10X10。這邊或許有人不太能了解。我另外舉個例子,某數A被某數B整除,那AX2也會是被B整除,AX3,AX11,AX124327也都會被B整除。再用實際的例子來說,21會被7整除,那21X2=42也會被7整除,21X3,21X11,21X124327也都會被7整除。整除就是餘0,同餘數就是相同的概念。會餘1的數乘上會餘1的數結果還是1X1會餘1,如果會餘1的數乘上會餘2的數的話,結果就會是餘2了。
那為什麼9的倍數的每個數字相加會等於9呢?
9x1=09
9x2=18=9+9因為要進位所以我們可以改寫成這樣9+1+(9-1)
9x3=27=9+9+9=(9+1+9+1)+(9-2)
9x4=36=9+9+9+9=(9+1+9+1+9+1)+(9-3)
所以當進位為十位數時,每增加1個十位數的同時,個位數就會減一個1。一加一減的結果使得9的倍數的每個數字相加起來會等於9。
又因為9=3X3所以3的倍數有類似的情況。3的倍數的每個數字相加起來會是3的倍數。
3X5=15,1+5=6
3x7=21,2+1=3
3X9=27,2+7=9
(二)倒著背。因式分解。
我們國小剛開始學九九乘法表,都是順著背。可是到了高年級,其實要有能力倒著背。國中時開始會計算幾個數字的最小公倍數及最大公因數,就要會因式分解。一些數字可以運用前面所說的方法來判斷是否是2,3,5,9的倍數。可是十進位法中的7是很討厭的數字,沒什麼規律可以投機取巧,就算運用同餘數的方法也是很麻煩。所以一眼看出某數是否是7的倍數就很有幫助了。49=7x7,這是很多國小生看不出來的因式分解。
為了讓我們更容易做因式分解,國小高年級的老師要我們背平方數,背到25X25=625,現在還記得361=19X19。
給視數學為大魔王的同學一個建議,理解有助記憶,記憶也有助理解。最苦幹實幹的做法就是抄題目及解答過程。當你熟悉整個流程時,你的解題技巧就會跟著進步。
(三)偶數與奇數。機率。
拉拉雜雜說了一大堆,總算要進入正題了!
讓我們再看一次九九乘法表。

九九乘法表是兩個個位數的相乘的結果,除了1不列入外,其餘都有。
那麼有個問題很有趣,這些相乘的結果,乘積,會是偶數還是奇數呢?
在我們做苦工一個一個看前。我們先想一想。
兩個個位數相乘的結果有哪幾種情況。兩個個位數都可以是奇數或偶數。
奇數X奇數=奇數
奇數X偶數=偶數
偶數X奇數=偶數
偶數X偶數=偶數
四種結果,只有一種是奇數。所以所有結果只有四分之一會是奇數,
又總共有8X9=72ˋ種結果,他的四分之一會是18。
所以九九乘法表中,只有18個結果是奇數。
讓我們做一下苦工吧,把奇數的結果框起來。
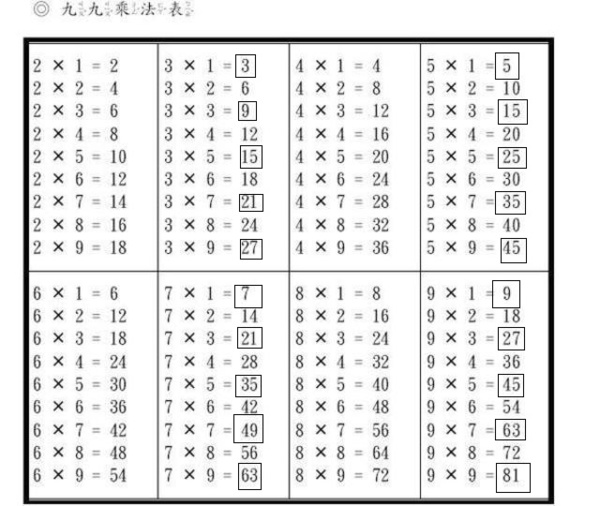
結果是20個,為什麼會有誤差呢?因為是從某數乘1一直乘到乘9。
如果是乘到10,8X10=80,80的四分之一是20,理論與實際結果就吻合了。

















