已知平面上３點座標，求三角形面積的題目是一種很特別的題目．
特別的地方在於這類題目從國一到高二都能找到方法來計算．
例：座標平面上Ａ（２,５）Ｂ（－１,１）Ｃ（５,－３），求△ＡＢＣ面積＝？
國一學生的一般做法：把圖形補成長方形或梯形然後去減三角形面積
如圖，梯形ＡＣＤＥ＝（３＋６）╳８／２＝３６
△ＡＢＥ＝３╳４／２＝６
△ＢＣＤ＝４╳６／２＝１２
３６－６－１２＝１８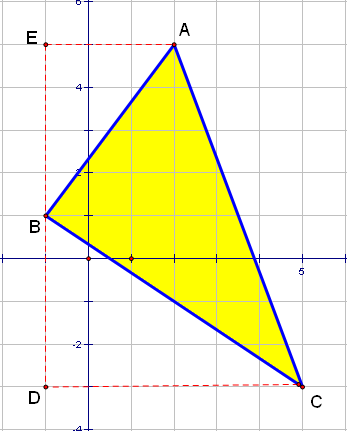
做法優點：下手容易
缺點：步驟較多，須有圖形輔助
少數國一學生的另一種做法：把圖形切成可以計算的圖形，再加總．
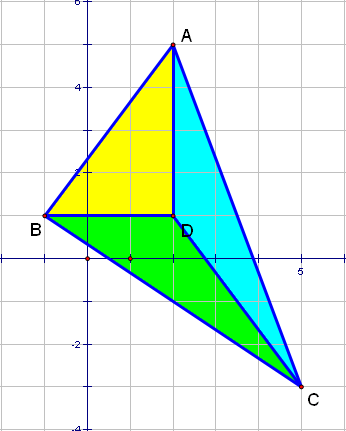
如圖，可以觀察出
△ＡＢＤ的底是３高是４
△ＢＣＤ的底是３高是４
△ＡＣＤ的底是４高是３
這三個三角形的底和高同是３和４的組合
所以，面積＝４╳３／２╳３＝１８．（三角形的合成）
做法優點：計算步驟極簡
條件：須有圖形輔助，還要有觀察力
少數國一學生可以偷用的做法：使用測量師公式（事實上是高中做法）
｜ ｜
１ ｜ ２ －１ ５ ２ ｜
△ＡＢＣ＝－｜｜ ｜｜
２ ｜ ５ １ －３ ５ ｜
｜ ｜
１
＝－＊｜（２＋３＋２５）－（－５＋５－６）｜
２
１
＝－＊３６＝１８
２
做法優點：萬能公式，只要有座標就能算
缺點：原理的說明較不容易
6樓. Ｌ˙Ｌａｗｌｉｅｔ2008/05/03 14:21標點！
使用測量師公式（事實上是高中做法）
這套作法。。。
我國１就會了
只是感覺這。。
平面座標太簡單了吧！
但是我都是在平面座標錯。。
因為眼睛＋算數有問題
哈。。
每次都是少算一格或多加一格。。
很囧吧！
5樓. 流浪紙鳶養肥貓2008/03/25 00:16再回應
所以現在教改後，已經很少出現需要複雜計算的題目了．
取而代之的是，需要細心觀察專心思考，但是計算簡單的題目．
這是時代趨勢．
－－－－－－－
這是個好趨勢
只想找一個空間，獨處…沒錯！是好趨勢．至少會讓數學不再那樣讓人生畏． 梅斯普雷爾 於 2008/03/25 23:47回覆
4樓. anybody2008/03/21 00:41報告老師
半夜算這個
真的有點吃力
不過久違的算法和公式都突然想起來了
-
3樓. 流浪紙鳶養肥貓2008/03/20 12:51我會選擇更笨的作法
去算底跟高
看到這個題目，突然察覺到…原來我都是這樣做數學的…最原始的公式和觀念…最複雜的數字和計算
只想找一個空間，獨處… 說真的，使用最原始最基本的觀念來算數學本身並沒有錯．只是複雜的數字和計算會扼殺了學生對數學的興趣．
所以我一向不主張用最基本的方法去土法煉鋼，那對學生來說，負擔大．
而且要用那方法來學習數學，真的得有很大的興趣支持．
所以現在教改後，已經很少出現需要複雜計算的題目了．
取而代之的是，需要細心觀察專心思考，但是計算簡單的題目．
這是時代趨勢．
梅斯普雷爾 於 2008/03/20 15:16回覆 
2樓. 五月的風2008/03/20 09:39..先匆看之
有時間再來思考一下...
不過~~能知道有不一樣的思考模式...感覺真不錯...
是啊！很高興您也能享受思考的樂趣．
梅斯普雷爾 於 2008/03/20 15:10回覆- 1樓.2008/03/20 08:03師兄阿
偶不想看到數字了 頭很痛溜~
最近算帳算到都是赤字耶
不知道下周六開會時會不會打起來
你這裡 擺些好玩的啦 要說說你小時候穿開檔褲偷尿尿的事 都行咩~
小三（咳～不要故意倒過來唸喔～）以前的事，我幾乎都不記得了．
只有還留著的小時後照片和我媽媽口傳的故事．
我才知道，小時後的我的樣子．
只是，照片不好看，就不獻醜了．
梅斯普雷爾 於 2008/03/20 15:10回覆
