狗吉拉自小就很喜歡的薛丁格 Schrodinger
                          
                           尤其喜歡他的貓


狗吉拉閱讀量子史話系列心得整理
......薛丁格 Schrodinger 的機率波意義

1924年
德布羅依 (de Broglie )提出一個假設 :
每一個粒子都具有波粒二象性
像電子、光子這些傳統上認為是粒子的主體
都具有這種波粒二象性質
也就是說
所有粒子在其粒子性存在時  都同時伴有一種物質波
粒子的能量與動量  會決定了它的物質波頻率與波長
(反向亦然)

聰明的 薛丁格 Schrodinger  跟著就開始動歪腦筋...
既然粒子具有波粒二象性
那就應該會有一個對應此一波性的波動方程式
能够描述粒子的量子行為

所以薛丁格 從 Hamilton & Jacobi 方程式下手
設計了一個非相對論性的方程式
再代入波函數  得到一個波動方程式

用此波動方程式來計算氫原子的光譜線分佈位置與強度
得到了與波耳能階模型計算出的相同答案
漂亮地證實了這個 波動方程式
可以描述量子層級裡的粒子行為

1926年
薛丁格正式把他的波動方程式與氫原子光譜分析結果
寫為一篇論文發表
(此波動方程式被稱為薛丁格波動方程
 Schrodinger equation )

但是他無法解釋這個波動方程式的物理意義
(薛丁格提出的解釋是粒子的電荷分佈密度假設)

就在論文發表之後
量子宗師 波恩(Max Born 不是哥本哈根派的 Bohr)  針對薛丁格波動方程式
提出了驚天動地的機率波概念(probability amplitude)
成功地解釋了薛丁格波動方程式 的物理意義
(雖然薛丁格本人不同意這樣的詮釋)


以下是狗吉拉個人對薛丁格波動方程式的機率波理解

這些理解  100%將會在某些部分是錯的
但尚不至於全部都錯
主要目的是僅供狗吉拉自己做筆記心得之用

首先
什麼叫波函數?
在數學裡面
用來描述波型的幾何函數 (如: sin, cos ...等等) 
都可以稱其為「波函數」

在古典的波函數(ψ)(x,t)中
給定一個時點 t 之下
可以理解到...
變數X的位置 與 因變數(質點)振動程度大小的相依關係

其相依關係的分佈就像個波一樣
有其波長與振幅


那麼什麼又叫 機率波函數 ?
機率波函數 
就是薛丁格用来
描述粒子所表現出的(德布羅依)物質波性質的函數

話說  量子宗師 波恩 在看到薛丁格波動方程之後
很厲害地 因勢利導地
借用了薛丁格方程中的波函數型式
做出一個量子力學上的重要假設 

他詮釋說...
波函數(ψ)值的平方就等於機率密度
波函數(ψ)值的平方
等價於粒子在該時點 該位置上的出現機率
(正確地說  是機率密度)

所以機率波函數是一種密度函數

這個機率 有大有小
此機率值的大小
正好符合
在數學上用來描述古典波動振幅大小的值
也就是
波函數(ψ)的數學型式
恰好能表達 (粒子出現)機率的分佈  (就是 數學=數學 的意思)

所以當我們說
量子力學薛丁格方程裡的波函數
是一種波動型式的機率波時
並不是在描述空間中真實存在的波動  (例 聲波  水波)
並不是真的指說
粒子像波一樣 透過介質 在空間裡震盪傳遞

反而是一種在數學上看起來像波的機率概念的東西
粒子在空間中某一個位置出現機會的分佈
就像個我們想像中的波的振幅一樣的分佈

更甚者...
透過波函數來描述粒子時 
並不是透過單一波長來描述
而是由很多不同波長的波 
加以線性組合(疊加)之後 共同描述 粒子

總結來說
波函數實際上是在描寫
物質受自身波動性的影響 
造成了自己在相空間裡有個在量子狀態下的分布情況

(此分布並非指統計物理裡
  對於大群粒子的總合行為的那種「分布」)

在觀念的類比上
我們可以想像...
粒子出現在某X位置的機率密度
就是 波在該X位置上
由波函數表示的振幅的平方值


對應上一篇的基本粒子雙狹縫實驗的詭異結果
我們現在可以試試以機率波來解答
為什麼屏幕上會有明暗干涉條紋這一部份的現象
(至於為什麼一旦偵測粒子  干涉條紋就消失這一點 仍無法解決)

應用機率波
物理學家可以真正計算出粒子抵達偵測屏幕的某個位置的機率

一個粒子的波前通過兩條狹縫後
這顆粒子會顯示於偵測屏障的某個位置的機率
可以由穿透兩條狹縫後的兩個機率波的疊加計算出來

當機率波的波前傳播至偵測屏障的某一點時
兩個機率波的疊加
決定了粒子會移動到那一個點的機率


以下
大家來看看波函數的真身

Ψ(x, t)

=A e-i(kx-ωt)=A e-iw(t-x/v)

=A cos w(t- x/v)- i  A sin w(t-x/v)

(這隻波 活在一種複數座標裡喔)

其中
(kx-ωt)為  相位角

k 的涵義就是 
波行進一個單位長度時  此單位長度內改變的相位角

k 的數值 也就是 2 π長度內有幾個波( k=2 π /λ)

要注意...
波函數Ψ(x, t)絕對值的平方
是機率密度
不是機率

而機率 = 機率密度 * 體積
機率是機率密度對整個空間作積分得到的
所以數學上  對波函數做正負無限的體積分 會等於 1

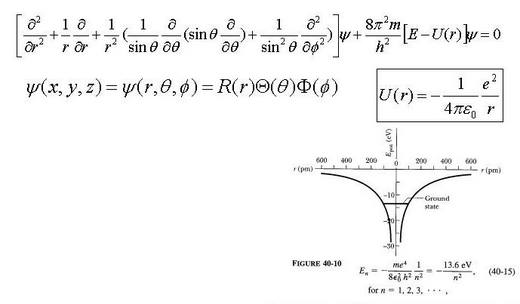
以下是  薛丁格波動方程  與  原子軌域上的機率密度波